По теме практического занятия №6

2015-12-07

555

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 1 2 3 4 5 67

Интегрирование тригонометрических функций.

1). Интегрирование вида , ,

находятся с помощью тригонометрических формул:

;

;

.

2) Интегралы вида , где и - четные числа, находятся с помощью формул: ; ; .

Если хотя бы одно из чисел и - нечетное, то интеграл находим непосредственно, отделяя от нечетной степени один множитель и вводя новую переменную. Например, если ,то .

3) Интегралы вида

где - рациональная функция от и 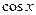, приводятся к интегралам от рациональных функций новой переменной с помощью подстановки 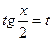, при этом , , .

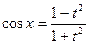Если , то целесообразно применять подстановку , при этом ; ; , .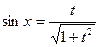

Интегрирование некоторых видов иррациональностей.

Простейшие интегралы от функций, содержащих иррациональности, являются табличными, либо сводятся к ним с использованием свойств интеграла и замены переменной. В более сложных случаях основной подход состоит в сведении искомого интеграла к интегралу от рациональной функции с помощью подходящей замены переменной (так называемой рационализации интеграла).

Интегралы вида , (где рациональная функция) находится с помощью подстановок соответственно , , .

Интеграл вида 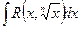реализуется с помощью замены .

Интегралы вида , где реализуются с помощью подстановки .

Вопросы для закрепления теоретического материала к практическому занятию:

1. Какие виды подстановок используются при интегрировании тригонометрических функций?

2. Перечислите основные приемы, используемые при интегрировании некоторых иррациональных функций.

Задания для практического занятия №6

Вариант №1.

1. Найдите интегралы следующих тригонометрических функций:

а) ; б) ; г) .

2. Найдите интегралы следующих иррациональных функций:

а) ; б) ; г) .

Вариант №2.

1. Найдите интегралы следующих тригонометрических функций:

а) ; б) ; в) .

2. Найдите интегралы следующих иррациональных функций:

а) ; б) ; в) .

Вариант №3.

1. Найдите интегралы следующих тригонометрических функций:

а) ; б) ; в) .

2. Найдите интегралы следующих иррациональных функций:

а) ; б) ; в) .

Вариант №4.

1. Найдите интегралы следующих тригонометрических функций:

а) ; б) ; в) .

2. Найдите интегралы следующих иррациональных функций:

а) ; б) ; в) .

Инструкция по выполнению практического занятия №6:

1. Прочитайте краткие теоретические и учебно-методические материалы по теме практического занятия.

2. Устно ответьте на вопросы для закрепления теоретического материала к практическому занятию.

3. Выберите свой вариант (задания для практического занятия).

4. Внимательно прочитайте каждое задание. Определите, к какому виду относятся данные интегралы.

5. При выполнении третьего задания обратитесь к кратким теоретическим и учебно-методическим материалам по теме практической работы и определите к какому виду относится заданный интеграл и выберете метод его вычисления.

6. При выполнении четвертого задания обратитесь к кратким теоретическим и учебно-методическим материалам по теме практической работы и определите к какому виду относится заданный интеграл и выберете метод его вычисления.

7. Проверьте правильность решения заданий.

8. Убедившись, что задания решены правильно на черновике, аккуратно спишите их в чистовик.

2015-12-07

555

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 1 2 3 4 5 67

Обсуждение в статье: По теме практического занятия №6

Обсуждений еще не было, будьте первым... ↓↓↓