 |
Главная |
Тема № 19. Определение обыкновенных ДУ. Общее и частное решение. Уравнения с разделёнными и разделяющимися переменными
|
из
5.00
|
Обыкновенным дифференциальным уравнением n – го порядка для функции y аргумента х называется соотношение вида
 (1.1),
(1.1),
Где F – заданная функция своих аргументов. В названии этого класса математических уравнений термин «дифференциальное» подчеркивает, что в них входят производные  (функции, образованные как результат дифференцирования); термин – «обыкновенное» говорит о том, что искомая
(функции, образованные как результат дифференцирования); термин – «обыкновенное» говорит о том, что искомая
функция зависит только от одного действительного аргумента.
Обыкновенное дифференциальное уравнение может не содержать в явном виде аргумент X, Искомую функцию  и любые ее производные, но старшая производная
и любые ее производные, но старшая производная  обязана входить в уравнение N-го порядка. Например
обязана входить в уравнение N-го порядка. Например
А)  – уравнение первого порядка;
– уравнение первого порядка;
Б)  – уравнение третьего порядка.
– уравнение третьего порядка.
При написании обыкновенных дифференциальных уравнений часто используются обозначения производных через дифференциалы:
В)  – уравнение второго порядка;
– уравнение второго порядка;
Г)  – уравнение первого порядка,
– уравнение первого порядка,
Функция 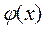 называется решением обыкновенного дифференциального уравнения, если при подстановке в него
называется решением обыкновенного дифференциального уравнения, если при подстановке в него  оно обращается в тождество.
оно обращается в тождество.
Например, уравнение 3-го порядка
 имеет решение
имеет решение  .
.
Решить обыкновенное дифференциальное уравнение – значит найти все функции, образующие при подстановке в уравнение тождество. Для уравнения (1.1) семейство таких функций образуется с помощью произвольных постоянных и называется общим решением обыкновенного дифференциального уравнения N-го порядка, причем число констант совпадает с порядком уравнения: 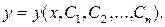 Общее решение может быть, и не разрешено явно относительно Y(X):
Общее решение может быть, и не разрешено явно относительно Y(X):  В этом случае решение принято называть общим интегралом уравнения (1.1).
В этом случае решение принято называть общим интегралом уравнения (1.1).
Например, общим решением дифференциального уравнения  является следующее
является следующее
выражение:  , причем второе слагаемое может быть записано и как
, причем второе слагаемое может быть записано и как  , так как произвольная постоянная
, так как произвольная постоянная  , делённая на 2, может быть заменена новой произвольной постоянной
, делённая на 2, может быть заменена новой произвольной постоянной  .
.
Задавая некоторые допустимые значения всем произвольным постоянным в общем решении или в общем интеграле, получаем определенную функцию, уже не содержащую произвольных констант. Эта функция называется частным решением или частным интегралом уравнения (1.1). Для отыскания значений произвольных постоянных, а следовательно, и частного решения, используются различные дополнительные условия к уравнению (1.1). Например, могут быть заданы так называемые начальные условия при  (1.2)
(1.2)
В правых частях начальных условий (1.2) заданы числовые значения функции и производных, причем, общее число начальных условий равно числу определяемых произвольных констант.
Задача отыскания частного решения уравнения (1.1) по начальным условиям называется задачей Коши.
§ 2. Обыкновенные дифференциальные уравнения 1-го порядка – основные понятия.
Обыкновенное дифференциальное уравнение 1-го порядка (N=1) имеет вид:  или, если его удается разрешить относительно производной:
или, если его удается разрешить относительно производной:  . Общее решение Y=Y(X,С) Или общий интеграл
. Общее решение Y=Y(X,С) Или общий интеграл 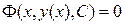 уравнения 1-го порядка содержат одну произвольную постоянную. Единственное начальное условие для уравнения 1-го порядка
уравнения 1-го порядка содержат одну произвольную постоянную. Единственное начальное условие для уравнения 1-го порядка  позволяет определить значение константы из общего решения или из общего интеграла. Таким образом, будет найдено частное решение или, что тоже, будет решена задача Коши. Вопрос о существовании и единственности решения задачи Коши является одним из центральных в общей теории обыкновенных дифференциальных уравнений. Для уравнения 1-го порядка, в частности, справедлива теорема, принимаемая здесь без доказательства.
позволяет определить значение константы из общего решения или из общего интеграла. Таким образом, будет найдено частное решение или, что тоже, будет решена задача Коши. Вопрос о существовании и единственности решения задачи Коши является одним из центральных в общей теории обыкновенных дифференциальных уравнений. Для уравнения 1-го порядка, в частности, справедлива теорема, принимаемая здесь без доказательства.
Теорема 2.1. Если в уравнении  функция
функция  и ее частная производная
и ее частная производная  непрерывны в некоторой области D плоскости XOY , и в этой области задана точка
непрерывны в некоторой области D плоскости XOY , и в этой области задана точка  , то существует и притом единственное решение
, то существует и притом единственное решение  , удовлетворяющее как уравнению
, удовлетворяющее как уравнению  , так и начальному условию
, так и начальному условию 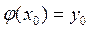 .
.
Геометрически общее решение уравнения 1-го порядка представляет собой семейство кривых на плоскости XOY, не имеющих общих точек и отличающихся друг от друга одним параметром – значением константы C. Эти кривые называются интегральными кривыми для данного уравнения. Интегральные кривые уравнения  обладают очевидным геометрическим свойством: в каждой точке
обладают очевидным геометрическим свойством: в каждой точке  тангенс угла наклона касательной к кривой равен значению правой части уравнения в этой точке:
тангенс угла наклона касательной к кривой равен значению правой части уравнения в этой точке:  . Другими словами, уравнение
. Другими словами, уравнение  задается в плоскости XOY поле направлений касательных к интегральным кривым. Замечание:Необходимо отметить, что к уравнению
задается в плоскости XOY поле направлений касательных к интегральным кривым. Замечание:Необходимо отметить, что к уравнению 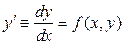 приводится уравнение
приводится уравнение  и так называемое уравнение в симметрической форме
и так называемое уравнение в симметрической форме  .
.
|
из
5.00
|
Обсуждение в статье: Тема № 19. Определение обыкновенных ДУ. Общее и частное решение. Уравнения с разделёнными и разделяющимися переменными |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

