 |
Главная |
Доказательство окончено. Определим число самодвойственных функций, имеющих n переменных
|
из
5.00
|
Пример.Пусть U =  . Тогда
. Тогда
U* =  .
.
Определим число самодвойственных функций, имеющих n переменных. Из условия самодвойственности следует, что на противоположных наборах значений переменных всякая  принимает противоположные значения. Поэтому всякая
принимает противоположные значения. Поэтому всякая  однозначно определяется своим заданием на наборах верхней половины табличного задания булевских функций n переменных, то есть на 2n-1 наборах.
однозначно определяется своим заданием на наборах верхней половины табличного задания булевских функций n переменных, то есть на 2n-1 наборах.
Следовательно, число функций n переменных вS равно  .
.
Покажем, что множество функций S является замкнутым классом. Поскольку тождественная функция f(x) = x является самодвойственной, то для доказательства замкнутости класса всех самодвойственных функций достаточно проверить, что если
h =  , где f, g1, . . . , gn - это самодвойственные функции, то h = h*.
, где f, g1, . . . , gn - это самодвойственные функции, то h = h*.
Воспользуемся теоремой о формуле для двойственной функции. Тогда h* =  = =
= =  = h, т.е. S -это замкнутый класс.
= h, т.е. S -это замкнутый класс.
Лемма (О несамодвойственной функции)
Если f  S, то подстановкой вместо переменных этой функции функций x и
S, то подстановкой вместо переменных этой функции функций x и  можно получить одну из функций констант.
можно получить одну из функций констант.
Доказательство
Пусть f  S. Тогда найдётся таких два противоположных набора
S. Тогда найдётся таких два противоположных набора  и
и  , что f
, что f 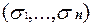 = f
= f 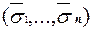 . Определим вспомогательные функции:
. Определим вспомогательные функции:
 , где i =1,..., n.
, где i =1,..., n.
Тогда функция h(x) = f(  совпадает с одной из функций констант.
совпадает с одной из функций констант.
Определим значения h(0) и h(1):
h(0) = f (  = f
= f 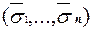 .
.
h(1) = f(  = f
= f 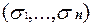 .
.
Следовательно, h(0) = h(1).
Доказательство окончено.
Замечание. Поскольку функции-константы не являются самодвойственными, то доказанная лемма утверждает, что из любой несамодвойственной функции можно получить простейшую несамодвойственную функцию.
Упражнение. Доказать утверждение, обратное утверждению, сформулированному в лемме о несамодвойственной функции.
МОНОТОННЫЕ ФУНКЦИИ
На множестве двоичных наборов длины n определим отношение предшествования наборов.
Пусть  и
и  . Тогда набор
. Тогда набор  предшествует набору
предшествует набору  , если
, если  .
.
Отношение предшествования наборов обозначается как  , т.е. значение каждой компоненты предшествующего набора не превосходит значения соответствующей компоненты следующего набора.
, т.е. значение каждой компоненты предшествующего набора не превосходит значения соответствующей компоненты следующего набора.
Например, наборы (0, 1, 0, 0, 1, 0) и (0, 1, 1, 0, 1, 1) находятся в отношении предшествования, а наборы
(1, 1, 0, 0, 1, 0) и (1, 0, 1, 0, 1, 1) оказываются несравнимыми в отношении  .
.
Упражнение. Проверить, что отношение предшествования наборов является отношением частичного порядка.
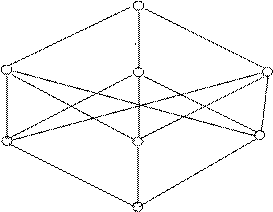
Рассмотрим представление отношения  на множестве
на множестве  с помощью диаграммы для этого отношения, представленной на рис 4.6. Пусть n = 3.
с помощью диаграммы для этого отношения, представленной на рис 4.6. Пусть n = 3.
1 1 1
 |
0 1 1 1 0 1 1 1 0
1 0 0 0 1 0 0 0 1
0 0 0
Рис. 4.6
На приведенной диаграмме не указана ориентация дуг, которые всегда считаются ориентированными в направлении верхней из двух вершин, соединяемых дугой.
Все наборы единичного n-мерного куба, имеющие равное число единиц, несравнимы между собой и образуют слой в таком кубе. В случае произвольного значения n в диаграмме для отношения  содержится n +1 слоев.
содержится n +1 слоев.
Упражнение. Нарисовать диаграмму отношения  для
для
n = 4.
ОПРЕДЕЛЕНИЕ
Булевская функция f(x1, . . . , xn) называется монотонной, если для любых наборов  и
и  , для которых
, для которых  , справедливо неравенство
, справедливо неравенство  .
.
Множество всех монотонных булевских функций обозначается как M.
Примеры.
1. Функция f (x1, x2)= x1 ® x2 немонотонна, так как
(0, 0)  (1, 0), но f(0, 0) > f (1, 0).
(1, 0), но f(0, 0) > f (1, 0).
2. Функции & и  являются монотонными.
являются монотонными.
Множество всех монотонных функций является замкнутым классом. Поскольку тождественная функция f(x) = x - монотонна, то для доказательства замкнутости M достаточно проверить, что при
h =  (1),
(1),
где f, g1 ,..., g n - монотонные функции,  M.
M.
Пусть x1, . . . , xn все различные символы переменных, которые встречаются в формуле (1). Возьмем два набора  и
и  значений этих переменных, для которых
значений этих переменных, для которых  . Тогда для наборов
. Тогда для наборов  и
и  , составленных из значений переменных функций g1, . . . , gn, взятых из наборов
, составленных из значений переменных функций g1, . . . , gn, взятых из наборов  и
и  , справедливы соотношения:
, справедливы соотношения: 
Следовательно,  для i = 1, . . . , n. Поэтому
для i = 1, . . . , n. Поэтому  . Поскольку
. Поскольку  M, то
M, то 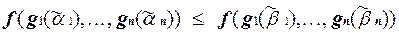 , т.е.
, т.е.  . Поэтому
. Поэтому  M.
M.
Замечание. Доказанное свойство монотонных функций позволяет просто устанавливать монотонность функций, представленных формулами составленными из монотонных функций. Например, монотонной является функция, представляемая формулой
 .
.
Простейшей немонотонной функцией можно считать функцию  , поскольку три остальные функции одной переменной являются монотонными. Покажем, что отрицание (или простейшая немонотонная функция) может быть получено из всякой немонотонной функции. Последнее свойство можно сформулировать иначе: всякая немонотонная функция содержит отрицание, которое может быть выражено из этой функции.
, поскольку три остальные функции одной переменной являются монотонными. Покажем, что отрицание (или простейшая немонотонная функция) может быть получено из всякой немонотонной функции. Последнее свойство можно сформулировать иначе: всякая немонотонная функция содержит отрицание, которое может быть выражено из этой функции.
Лемма. (О немонотонной функции)
Если 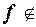 M, то подстановкой вместо переменных этой функции функций-констант и тождественной функции f(x) = x можно получить функцию
M, то подстановкой вместо переменных этой функции функций-констант и тождественной функции f(x) = x можно получить функцию  .
.
Доказательство
Пусть f(x1,...,xn)  M. Тогда найдутся такие два набора
M. Тогда найдутся такие два набора  и
и  значений переменных x1,. . . , xn, что
значений переменных x1,. . . , xn, что  и
и  . Возьмем эти наборы. Предположим, что они различаются в k компонентах.
. Возьмем эти наборы. Предположим, что они различаются в k компонентах.
Построим цепочку двоичных наборов, последовательно заменяя значения 0, 1, . . . , k разрядов, в которых набор  отличается от набора
отличается от набора  :
:
 . (1)
. (1)
Очевидно, что всякие два соседних набора этой последовательности различаются ровно в одной компоненте.
Рассмотрим значения f на наборах цепочки (1).
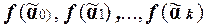 . (2)
. (2)
Поскольку  и
и  , то в (2) найдутся последовательно идущие значения 1 и 0.
, то в (2) найдутся последовательно идущие значения 1 и 0.
Рассмотрим наборы  =
=  и
и  = =
= =  , на которых функция f принимает значения 1 и 0.
, на которых функция f принимает значения 1 и 0.
Тогда  .
.
Действительно,
h (0) = h  = 1 и
= 1 и
h (1) = h  )= 0.
)= 0.
Доказательство окончено.
Замечание. Двоичные наборы, различающиеся лишь в одной компоненте, называются соседними. Доказательство последней леммы позволяет утверждать, что для всякой немонотонной функции найдутся таких два соседних набора, на которых нарушается монотонность.
Рассмотрим пример использования леммы о немонотонной функции. Пусть задана функция f = x1 ® (x2® x3). Тогда наборы
(0, 1, 0) и (1, 1, 0) являются соседними и на этих наборах нарушается монотонность f:
f(0, 1, 0) = 1иf(1, 1, 0) = 0.
Поэтому f(x, 1, 0) =  .
.
Упражнение.
1. Докажите утверждение, обратное утверждению, сформулированному в лемме о немонотонной функции.
2. Проверьте справедливость следующего утверждения: Если ф.а.л. f(x1,...,xn) отличнаот тождественной единицы, то всякая минимальная ДНФ для f не содержит элементарных конъюнкций, содержащих отрицания переменных.
ЛИНЕЙНЫЕ ФУНКЦИИ
Напомним, что линейными называются функции, представимые в виде  , где a1, . . . , an+1 - двоичные коэффициенты при переменных и свободном члене, равном 1.
, где a1, . . . , an+1 - двоичные коэффициенты при переменных и свободном члене, равном 1.
Класс линейных функций обозначается как L.
Из установленного способа представления линейных функций следует, что существует ровно 2n+1 различных линейных функций, зависящих от n переменных. Действительно, записи линейных функций являются частным случаем полиномов Жегалкина, поэтому представление всякой линейной функции в виде  единственное. Поэтому линейных функций от n переменных ровно столько, сколько имеется способов составления различных записей вида:
единственное. Поэтому линейных функций от n переменных ровно столько, сколько имеется способов составления различных записей вида:  .
.
Класс L является замкнутым, поскольку преобразование всякой суперпозиции линейных функций к виду полинома Жегалкина не приводит к появлению нелинейных слагаемых.
Замечание. Только две линейные функции n переменных существенно зависят от всех своих переменных:
 и
и 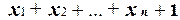 .
.
Всякая другая линейная функция n переменных, полином Жегалкина для которых не содержит вхождения некоторых переменных, имеет несущественные переменные.
Все 4 функции одной переменной: 0, 1, x и  являются линейными.
являются линейными.
Простейшим примером нелинейной функции можно считать x1&x2, поскольку ее представление в виде полинома Жегалкина содержит одно произведение переменных. Покажем, что эта простейшая нелинейная функция может быть выражена из любой нелинейной функции.
Лемма (О нелинейной функции)
Если f(x1, . . . , xn)  L, то подстановкой вместо переменных этой функции функций-констант 0, 1, тождественных функции x и отрицанию
L, то подстановкой вместо переменных этой функции функций-констант 0, 1, тождественных функции x и отрицанию  , а также применением отрицания к f можно получить функцию
, а также применением отрицания к f можно получить функцию  .
.
Доказательство
Пусть f(x1, . . . , xn)  L.
L.
Возьмем полином Жегалкина R для f. Так как f - это нелинейная функция, то в полиноме R содержится слагаемое, включающее произведение некоторых двух переменных. Без ограничения общности можно считать, что такое произведение содержит вхождения переменных x1и x2.
(Если все произведения двух и большего числа переменных не содержат одновременно эти переменные, то необходимо произвести соответствующее переименование переменных в f, используя подстановки переменных вместо переменных функции.)
Сгруппируем слагаемые в R и, вынося переменные x1 и x2 за скобки, представим его в виде
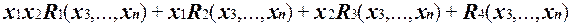 (1).
(1).
Здесь полином R1 содержит хотя бы одно ненулевое слагаемое и поэтому представляет булевскую функцию, отличную от тождественного нуля.
Пусть  . Подставим вместо переменных x3, . . . , xn конкретные значения
. Подставим вместо переменных x3, . . . , xn конкретные значения  . Тогда имеет место равенство:
. Тогда имеет место равенство:
 =
=  (2)
(2)
Здесь 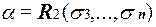 и
и 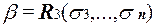 .
.
Заменим x1 на x1 + b и х2 на x2 +a. При этом, если a или b, равно нулю, то соответствующая переменная не заменяется. В противном случае соответствующая переменная заменяется на отрицание этой переменной.
В результате такой замены выражение (2) преобразуется к виду
 . (3)
. (3)
Если  , то функция x1&x2уже получена.
, то функция x1&x2уже получена.
В противном случае применим отрицание к функции вида (3) и также получим x1&x2.
|
из
5.00
|
Обсуждение в статье: Доказательство окончено. Определим число самодвойственных функций, имеющих n переменных |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

