 |
Главная |
Наибольший общий делитель двух многочленов
|
из
5.00
|
Многочлен R(x) называется общим делителем для многочленов P(x) и Q(x), если он служит делителем для каждого из этих многочленов. Согласно свойству (4) общими делителями произвольных многочленовP(x) и Q(x) будут все многочлены нулевой степени (т.е. все действительные числа за исключением числа 0). Если других общих делителей два многочлена не имеют, то эти многочлены называются взаимно простыми.
Наибольшим общим делителем многочленов P(x) и Q(x) называется такой многочлен D(x), который является их общим делителем и вместе с тем сам делится на любой общий делитель этих многочленов.
Если D(x) является наибольшим общим делителем многочленов P(x) и Q(x), то наибольшим общим делителем этих многочленов будет и многочлен cD(x), где c - произвольное число, отличное от нуля, т.е. наибольший общий делитель двух многочленов определен лишь с точностью до постоянного множителя. Чтобы добиться полной однозначности в определении наибольшего общего делителя двух многочленов, обычно выставляют следующее условие: из всех многочленов cD(x) наибольшим общим делителем называется тот, у которого старший коэффициент равен единице.
Теперь можно сказать, что два многочлена являются взаимно простыми, если их наибольший общий делитель равен единице.
Алгоритм Евклида (алгоритм последовательного деления) нахождения наибольшего общего делителя многочленов f(x) и g(x)

Тогда  - наибольший общий делитель f(x) и g(x).
- наибольший общий делитель f(x) и g(x).
1.16
Схема Горнера
Если  то при делении f(x) на g(x) частное q(x) имеет вид
то при делении f(x) на g(x) частное q(x) имеет вид

где  Остаток r находится по формуле
Остаток r находится по формуле 

1.17
Следствие
Немедленным следствием из теоремы является то, что любой многочлен степени  над полем комплексных чисел имеет в нём ровно
над полем комплексных чисел имеет в нём ровно  корней, с учётом кратности корней.
корней, с учётом кратности корней.
Доказательство.
У многочлена  есть корень
есть корень  , значит, по теореме Безу, он представим в виде
, значит, по теореме Безу, он представим в виде  , где
, где  — другой многочлен. Применим теорему к
— другой многочлен. Применим теорему к  и будем применять её таким же образом до тех пор, пока на месте
и будем применять её таким же образом до тех пор, пока на месте  не окажется линейный множитель.
не окажется линейный множитель.
Доказательство.
Представим полином  в виде суммы
в виде суммы  , где
, где  ,
, 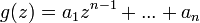 . Составим соотношение
. Составим соотношение 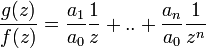 . Легко видеть, что для любых коэффициентов
. Легко видеть, что для любых коэффициентов  всегда найдется такое значение
всегда найдется такое значение  , что для всех значений
, что для всех значений 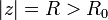 имеет место неравенство
имеет место неравенство  . В силу теоремы Руше следует, что полное число нулей функции
. В силу теоремы Руше следует, что полное число нулей функции 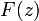 в круге
в круге  равно числу нулей в этом круге функции
равно числу нулей в этом круге функции  . Но функция
. Но функция  на всей комплексной плоскости имеет один единственный n-кратный корень
на всей комплексной плоскости имеет один единственный n-кратный корень 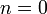 . Отсюда, в силу произвольности
. Отсюда, в силу произвольности  и следует утверждение теоремы.
и следует утверждение теоремы.
Формулы Виета
Если  и
и 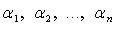 - корни многочлена (каждый кратный корень взят здесь столько раз, какова его кратность), то:
- корни многочлена (каждый кратный корень взят здесь столько раз, какова его кратность), то:
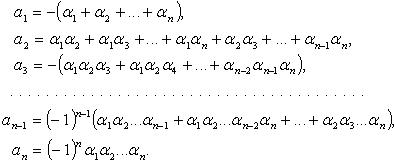
В частности, при 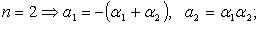 при
при 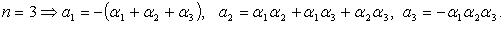
1.18
|
из
5.00
|
Обсуждение в статье: Наибольший общий делитель двух многочленов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

