САМОСТОЯТЕЛЬНАЯ РАБОТА

Темы, формы контроля и объём часов на самостоятельную работу

ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ

1. Понятие множества. Операции над множествами. Функциональная зависимость. Способы задания функций. Сложная функция.

2. Классификация функций: чётные и нечётные, периодические и непериодические. Ограниченные функции. Наибольшее и наименьшее значения функции. Монотонность функций. Обратная функция.

3. Графики основных элементарных функций (линейной, модуля, квадратичной, степенной, показательной, логарифмической, тригонометрических, обратных тригонометрических функций). Функции полезности, спроса и предложения.

4. Числовые последовательности. Ограниченные и неограниченные последовательности. Предел числовой последовательности. Арифметические операции над пределами.

5. Сумма бесконечно убывающей геометрической прогрессии. Монотонные последовательности. Число 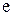. Задача о непрерывном начислении процентов.

6. Предел функции в точке. Два замечательных предела.

7. Непрерывность функции в точке. Арифметические действия над непрерывными функциями.

8. Непрерывность функции на множестве. Непрерывность некоторых элементарных функций. Точки разрыва функций, их классификация.

9. Глобальные свойства непрерывных функций: теорема об ограниченности функции, заданной и непрерывной на отрезке, теорема о достижении функцией, непрерывной на отрезке, своих наибольшего и наименьшего значений.

10. Производная и дифференциал. Геометрический, физический, экономический смысл производной. Зависимость между непрерывностью и дифференцируемостью функции. Производные высших порядков.

11. Схема вычисления производной. Правила дифференцирования. Производная основных элементарных функций.

12. Производная сложной и обратной функций.

13. Основные теоремы о дифференцируемых функциях (теоремы Ферма, Ролля и Лагранжа, правило Лопиталя).

14. Возрастание и убывание функций. Экстремум функции. Схема исследования функции на экстремум. Отыскание наибольшего и наименьшего значений функции, заданной на отрезке.

15. Выпуклость функции и точки перегиба. Схема исследования функции на выпуклость и точки перегиба.

16. Асимптоты. Общая схема исследования функций и построения их графиков.

17. Первообразная функция и неопределенный интеграл. Свойства неопределённого интеграла. Неопределённый интеграл от основных элементарных функций.

18. Интегрирование заменой переменного и по частям. Интегрирование рациональных функций.

19. Интегрирование некоторых иррациональных функций и тригонометрических выражений.

20. Понятие определённого интеграла, его геометрический и экономический смысл. Свойства определённого интеграла. Формула Ньютона-Лейбница.

21. Замена переменного и формула интегрирования по частям в определённом интеграле.

22. Несобственные интегралы.

23. Понятие функции многих переменных. Область определения, линии уровня. Функции полезности и кривые безразличия. Производственная функция и изокванты.

24. Предел и непрерывность функций многих переменных.

25. Частные производные. Дифференциалы функций многих переменных. Производная по направлению, градиент.

26. Локальный экстремум, наибольшее и наименьшее значения функций многих переменных.

27. Условный экстремум: метод подстановки и метод множителей Лагранжа.

28. Метод наименьших квадратов.

29. Бесконечно убывающая геометрическая прогрессия. Числовые ряды. Сходимость ряда. Необходимый признак сходимости ряда.

30. Признаки сходимости рядов с положительными членами (признаки сравнения, интегральный признак, признаки Коши и Даламбера).

31. Знакопеременные ряды. Абсолютная сходимость и условная. Признак Лейбница.

32. Функциональные ряды. Область сходимости функционального ряда. Степенные ряды. Интервал сходимости степенного ряда.

33. Разложение в ряды Маклорена некоторых функций.

34. Дифференциальные уравнения первого порядка. Теорема существования и единственности. Уравнения с разделяющимися переменными.

35. Линейные уравнения первого порядка.

36. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами (случай простых корней и кратных корней).

37. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

38. Линейные системы дифференциальных уравнений с постоянными коэффициентами.