Программу требуется переделать. Написать ИМЕННО для 2 класса

Диагностические работы «Задания»

Аналитический уровень

Для выполнения задания вам дан конспект урока.

Определите тему урока по представленному конспекту и планируемые предметные и метапредметные результаты, которые достигались на данном уроке.

В таблице №3 укажите тему урока, укажите достигаемые на уроке предметные и конкретные метапредметные результаты и какие задания на уроке подтверждают ваш выбор.

Конспект урока:

Этап урока	Деятельность учителя	Деятельность учащихся
1.Психологический настрой на урок.	Прозвенел и смолк звонок. Начинается урок. -Ребята! Мы знаем, что в математике нет царских дорог, все идут одним путём – терпение и труд. И чтобы сделать, надо делать! – наш девиз. -Улыбнитесь друг другу, пожелайте удачи. Постарайтесь работать быстро, все расчёты производить точно и, самое главное, дружно!
2. Актуализация познавательной деятельности.     3. Создание проблемной ситуации. Постановка учебной задачи. 4. Решение учебной задачи (выдвижение и проверка гипотез).	– Ребята! Над какой проблемой мы работали на предыдущих уроках математики?   Что было задано на дом?   - Кто желает прокомментировать решение задачи? - Дети! У кого были трудности? - Посмотрите, я приготовила для вас интересное задание: Даны уравнения. 20 + х = 36 2 · х = 46 х + 10 = 72 х = 36 + 20 х = 42· 2 х = 72 - 10 х = 36 х = 84 х = 62 - Известно, что среди этих уравнений только одно верно. Сумеете отыскать его за одну минуту? - Расскажите на математическом языке, как решали уравнения! Объясните свой способ действия. - оцените свои действия!   -А я предлагаю вам решить ещё одно уравнение. 10 + 2 · х =36 - Что заметили? Чем похожи эти уравнения?   - Кто попробует решить это уравнение? - Так в чём проблема? Чем данное уравнение отличается от предыдущих?     - Сформулируйте тему урока.   - Какую учебную задачу будем решать на уроке? - Как будем решать поставленную задачу? Давайте искать способ действия. Определите главную операцию и её компоненты.   (учитель фиксирует их на доске, а верную записывает последней).   - Можно ли сразу получить простое уравнение? - А можете ли вы их упростить? Как?   - Давайте попробуем. - Каких знаний не хватает, чтобы справиться с возникшей проблемой? - Давайте составим памятку – алгоритм для решения сложных уравнений. - Да, ребята, помните, при решении сложного уравнения очень важен порядок действий, определение главной операции, а также компоненты. Алгоритм решения сложных уравнений. 1.Определяем порядок действий. Разбиваем выражение на части. 2. Определяем неизвестное по последнему действию. 3.Обводим кружком целое, выделяем части. (Смотрим, что надо найти – целое или части) 4. Решаем как простое уравнение. 5. Записываем ответ.       - Какое открытие мы сделали?	- Учились решать задачи на процессы при помощи уравнений. - Творческая работа: зная возможные скорости движения, составить и решить задачу при помощи простого уравнения. Три ученика у доски рассказывают о выполнении домашнего задания. Выделяют собственные трудности   Дети работают самостоятельно. Попробуем! Выслушиваются и обсуждаются варианты ответов детей. Верное третье уравнения, чтобы его найти, нам нужно было выделить части и целое в каждом уравнении.   - Числа одинаковые, действия одинаковые. (к доске идёт ученик). У доски ученик затрудняется решить уравнение. - Уравнение сложное, в той части, где х – два действия. Уравнения такого вида мы ещё не решали. - Решение сложных уравнений. - Научиться решать сложные уравнения нового вида. Дети предлагают свои гипотезы (Обсуждение и проверка различных гипотез, поступивших от детей). - Надо от сложного уравнения перейти к простому, ведь простые уравнения мы умеем решать. - Нет. - Я считаю, что сложное уравнение надо упростить.   - Может расставить порядок действий и посмотреть на последнее действие. - У нас нет алгоритма решения сложного уравнения.   ( в результате выводится алгоритм решения сложных уравнений).   (Одновременно с объяснением идёт фиксация результатов на доске в виде решения уравнения). 10 + 2· х = 36 последнее действие сложение, значит, 10 это часть, 2 · х тоже часть, а 36 - целое; 2· х = 36 – 10 чтобы найти часть, надо из целого отнять известную часть; 2 · х = 26 это простое уравнение, неизвестен второй множитель. х = 26 : 2 чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. х = 13 после решения обязательно сделаю проверку. 10 + 2 · 13 = 36 36 = 36 уравнение решено верно. - Нашли способ решения сложных уравнений.
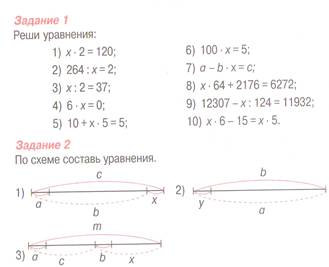
5. Работа по теме урока. Отработка способа действия.	- Как вы считаете, нужно ли упражняться в решении сложных уравнений? - Давайте потренируемся. -Распределите уравнения в 2 группы так, чтобы в 1 группе были уравнения простые, а во 2 группе сложные уравнения. Выберите те уравнения сложные, которые вы можете решить по алгоритму. -Как будем работать?	- Да. Обучающиеся выполняют задание     - Давайте будем в паре работать, потому что мы еще не уверены, что сами сможем решить уравнения. Сначала мы в паре решим, а потом сверим наши работы.
9. Итог урока. Рефлексия.	- Какую учебную задачу ставили? - Что для вас сегодня было открытием? -Сегодня мы с вами раскрыли ещё один секрет математики. - Всем ли было легко? - Значит надо ещё потренироваться? - Над какой же проблемой будем работать на следующем уроке? - Давайте подведём итог урока, закончив предложения:   Я сегодня научился….. Я узнал……. Больше всего мне понравилось….	Ответы детей на поставленные вопросы.   Несколько человек подняли руки, высказались о своих трудностях.   - Продолжить работу по решению сложных уравнений.

Заполните таблицу

Таблица №3

Тема урока: Решение сложных уравнений
Примеры видов деятельности учащихся и заданий	предметные результаты, формируемые на данном задании	метапредметные результаты, формируемые на данном задании
Даны уравнения. 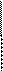20 + х = 36 2 · х = 46 х + 10 = 72 х = 36 + 20 х = 42· 2 х = 72 - 10 х = 36 х = 84 х = 62 Найти уравнение с верным решением.	Демонстрируют умение определять правильность решения простых уравнений	Анализируют объекты
вам решить ещё одно уравнение. 10 + 2 · х =36 - Что заметили? Чем похожи эти уравнения? (сравнивают с предыдущими, простыми уравнениями).	Открывают способ решения сложных уравнений	Сравнивают объекты по существенным признакам.
- Какую учебную задачу будем решать на уроке? - Как будем решать поставленную задачу?		Осуществляют постановку учебной задачи под руководством учителя
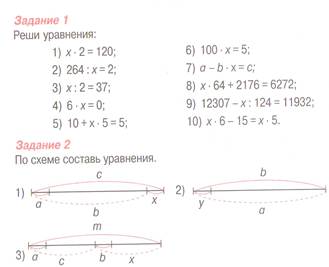
Выберите те уравнения сложные, которые вы можете решить по алгоритму. -Как будем работать?	Решают сложные уравнения     …[A3]	Действуют по составленному ранее алгоритму
- Всем ли было легко? - Значит надо ещё потренироваться? - Над какой же проблемой будем работать на следующем уроке? - Давайте подведём итог урока, закончив предложения:   Я сегодня научился….. Я узнал……. Больше всего мне понравилось….		Рефлектируют результат собственной деятельности   …[A4]