Примеры решения типовых задач

Классическая формула вероятности. Основные теоремы теории вероятностей

На шести карточках написаны буквы Т И Л А Б Е. найти вероятность того, что, из взятых по порядку пяти карточек можно составить слово «билет».

Решение:

Из данных 6 букв можно составить слова по 5 букв по формуле числа перестановок без повторений:

Поэтому появление слова «билет» определяется:

В коробке 5 синих, 4 красных и 3 зеленых карандаша. Наудачу вынимают 3 карандаша. Какова вероятность того, что:

а) Все они одного цвета;

б) Все они разных цветов;

в) Среди них 2 синих и 1 зеленый карандаш.

Решение:

Решение:

Сначала заметим, что число способов выбрать 3 карандаша из 12 имеющихся в наличии равно:

а) Выбрать 3 синих карандаша из 5 можно способами;

3 красных из 4 можно способами;

3 зеленых из 3 можно способами.

По правилу сложения общее число случаев, благоприятствующих событию

равно

б) равно

в) равно

 

Для уничтожения колонии паразитов ее обрабатывают последовательно двумя препаратами. Вероятность уничтожения колоний первым препаратом – 0,4; вторым – 0,6, причем их действие независимы.

а) найти вероятность того, что после действия обоих препаратов колония не будет уничтожена.

б) найти вероятность того, что после действия обоих препаратов колония будет уничтожена.

Решение:

События:

колония уничтожится 1-ым препаратом;

колония уничтожится 2-ым препаратом; тогда

–вероятность уничтожения колонии 1-ым препаратом;

–вероятность уничтожения колонии 2-ым препаратом;

Тогда вероятность того, что колония не уничтожится 1-ым препаратом;

вероятность того, что колония не уничтожится 2-ым препаратом;

а) Вероятность того, что после действия обоих препаратов колония не уничтожится, учитывая независимость событий, вычисляется по формуле:

б) Вероятность того, что после действия обоих препаратов колония уничтожится, учитывая независимость событий, вычисляется по формуле:

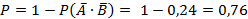
Ответ: а) Р=0,24; б) Р=0,76

 

Три стрелка делают по одному выстрелу в цель. Вероятность попадания для первого стрелка 0,8, для второго – 0,7, для третьего – 0,6. Найти вероятность того, что:

а) все стрелки попадут в цель;

б) только один стрелок попадет в цель;

в) только два стрелка попадут в цель;

г) все стрелки промахнутся;

д) цель будет поражена.

Решение:

Обозначим: событие А – первый стрелок попадет в цель

B – второй стрелок попадет в цель

С – третий стрелок попадет в цель

События A, B, C – независимые.

а)

б)

в)

г)

д)

 

Полная вероятность. Формула Байеса

Рабочие обслуживают три станка, на которых обрабатывается однотипные детали. Вероятность изготовления бракованной детали на первом станке равна 0,02, на втором – 0,03, на третьем – 0,04. Обработанные детали складываются в один ящик.

Производительность первого станка в три раза больше чем второго, а третьего – в два раза меньше чем второго. Взятая на удачу деталь оказалась бракованной. Найти вероятность того, что она изготовлена на третьем станке.

Решение:

Событие .

Деталь может быть изготовлена на первом, втором или третьем станке соответственно с вероятностями:

Условная вероятность того, что бракованная деталь изготовлена первым станком:

По формуле полной вероятности

По формуле Бейеса

Ответ:

 

Два консервных завода поставляют в магазин мясные и овощные консервы, причем первый завод поставляет продукции в три раза больше второго. Доля овощных консервов в продукции первого завода составляет 60%, а второго 70%. Для контроля в магазине взято наугад одно изделие.

а) Какова вероятность того, что это окажутся мясные консервы?

б) Взятое изделие оказалось мясными консервами. Какова вероятность, что оно изготовлено вторым заводом?

Решение:

Обозначим событие

По условию задачи первый завод поставляет продукции в три раза больше, чем второй, то есть в три раза, или

Вероятность того, что консервы мясные, для первого завода составляет 40%, то есть , для второго завода 30%, то есть .

а) Учитывая, что событие А произойдет обязательно с одним из событий (гипотез) Н_i, образующих полную группу, применим формулу полной вероятности:

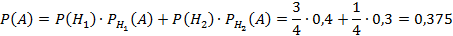
б) По условию событие А произошло, то есть взяты мясные консервы. Тогда вероятность гипотезы Н₂ – консервы изготовлены вторым заводом – находим по формуле Байеса

 

Из 27 частных банков нарушения в уплате налогов имеют место 13 банках. Проверяют 3 банка, выбирая их случайным образом из 27 банков. Выбранные банки проверяются независимо друг от друга. Нарушения выявляются с вероятностью 0,7. Какова вероятность того, что в ходе проверки будет установлен факт наличия банков, допускающих нарушения.