Пример расчета экстремума функции методом прямого поиска Хука-Дживса

Постановка задачи. Определить экстремум функции f(x)=(x₁-2)⁴+( x₁-2x₂)² с точностью e=0,05 для начального приближения Х⁽⁰⁾=[2.5; 2.5].

Расчет экстремума методом Хука-Дживса для поставленной задачи реализован средствами EXСEL. Результаты расчета представлены в таблице 2.2, а траектория поиска приведена на рисунке 2.2.

 

Таблица 2.2.

Результаты расчетов минимума функции f(x)=(x₁-2)⁴+( x₁-2x₂)² методом Хука-Дживса.

Исследующий поиск
№	х1	х2	f(X)	S1	S2	λ1	λ2
	2.500	2.500	6.3125	0.500	-1.000	0.0500	-0.100
3.000	1.500	1.0000
Поиск по образцу
№	х1	х2	f(X)	λ1	λ2	||X(k+1) - X(k)||	Критерий
	2.500	2.500	6.3125	0.05	-0.1	1.0125	Не достигнут
	2.550	2.400	5.1540
	2.600	2.300	4.1296
	2.650	2.200	3.2410
	2.700	2.100	2.4901
	2.750	2.000	1.8789
	2.800	1.900	1.4096
	2.850	1.800	1.0845
	2.900	1.700	0.9061
	2.950	1.600	0.8770
	3.000	1.500	1.0000
Исследующий поиск
№	х1	х2	f(X)	S1	S2	λ1	λ2
	2.950	1.600	0.8770	-0.300	-0.275	-0.03	-0.0275
2.650	1.375	0.1885
Поиск по образцу
№	х1	х2	f(X)	λ1	λ2	||X(k+1) - X(k)||	Критерий
	2.950	1.600	0.8770	-0.03	-0.0275	0.5049	Не достигнут
	2.920	1.573	0.7670
	2.890	1.545	0.6674
	2.860	1.518	0.5777
	2.830	1.490	0.4971
	2.800	1.463	0.4253
	2.770	1.435	0.3616
	2.740	1.408	0.3055
	2.710	1.380	0.2566
	2.680	1.353	0.2144
	2.650	1.325	0.1785
	2.620	1.298	0.1484
	2.590	1.270	0.1236
	2.560	1.243	0.1039
	2.530	1.215	0.0888
	2.500	1.188	0.0780
	2.470	1.160	0.0712
	2.440	1.133	0.0680
	2.410	1.105	0.0681
Исследующий поиск
№	х1	х2	f(X)	S1	S2	λ1	λ2
	2.440	1.133	0.0680	-0.201	-0.013	-0.0201	-0.0013
2.239	1.119	0.0033
Поиск по образцу
№	х1	х2	f(X)	λ1	λ2	||X(k+1) - X(k)||	Критерий
	2.440	1.133	0.0680	-0.0201	-0.0013	0.0492	Достигнут
	2.420	1.131	0.0558
	2.400	1.130	0.0451
	2.380	1.129	0.0357
	2.360	1.127	0.0277
	2.339	1.126	0.0209
	2.319	1.125	0.0153
	2.299	1.123	0.0108
	2.279	1.122	0.0073
	2.259	1.121	0.0048
	2.239	1.119	0.0033
	2.219	1.118	0.0026
	2.199	1.117	0.0028

Таким образом, из таблицы видно, что экстремум найден на третьей итерации, точка [2.199;1.117] является минимумом заданной функции с точностью 0,05.

 

 

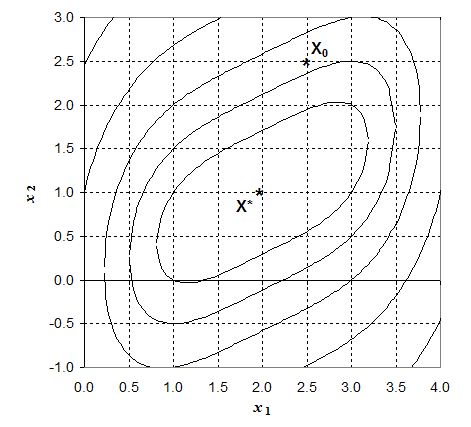Рис.2.2. Графическая иллюстрация поиска экстремума функции методом прямого поиска Хука-Дживса.

Метод Розенброка

Метод Розенброка является итерационной процедурой, имеющей некоторое сходство с исследующим поиском Хука и Дживса. Отличие состоит в том, что с помощью дискретных шагов или одномерной оптимизации поиски осуществляются вдоль системы ортонормированных направлений S₁^(k), …, S_n^(k), полученных при помощи процедуры Грама-Шмидта.

На первой итерации процесс поиска из начального приближения X⁽¹⁾ осуществляется вдоль координатных осей. Результатом этого процесса будет точка X⁽²⁾. После этого происходит смена направлений. Причем единичный вектор направления совпадает с вектором перехода из X⁽¹⁾ в X⁽²⁾, а достраивается ортогонально к . В общем случае набор ортонормированных векторов на (k+1)-м этапе вычисляется при помощи следующих соотношений

;

;

;

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

;

,

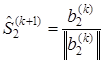где ||a_i|| - норма a_i, являющаяся вектором перехода из X^(k) в X^(k+1) по направлениям.

Векторы a_i рассчитываются по формуле:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

где - величина шага, равная переходу из X^(k) в X^(k+1) по направлениям.

Алгоритм метода Розенброка с минимизацией по направлению.

Начальный этап. Пусть e> 0 - скаляр, используемый в критерии остановки. Выбрать в качестве координатные направления, начальную точку X⁽¹⁾, положить Y⁽¹⁾ = X⁽¹⁾, k = j = 1 и перейти к основному этапу.

Основной этап. Шаг 1. Найти l_j^* - оптимальное решение задачи минимизации f(Y^(j) + l_j ) и положить Y^(j+1) = Y^(j) + l_j^* . Если j < n, то заменить j на j + 1 и вернуться к шагу 1. В противном случае перейти к шагу 2.

Шаг 2. Положить X^(k+1) = Y⁽ⁿ⁺¹⁾. Если ||X^(k+1) - X^(k)|| < e, то остановиться; в противном случае положить Y⁽¹⁾ = X^(k+1), заменить k на k + 1, положить j = 1 и перейти к шагу 3.

Шаг 3. Построить новое множество линейно независимых и взаимно ортогональных направлений в соответствии с (2.5) и (2.6). Обозначить новые направления через и вернуться к шагу 1.

Алгоритм метода Розенброка с дискретным шагом.

Начальный этап. Выбрать число e> 0 для остановки алгоритма, коэффициент растяжения a>1 и коэффициент сжатия bÎ (-1, 0). Взять в качестве координатные направления и выбрать l₁, …, l_n >0 начальную длину шага вдоль каждого из направлений. Выбрать начальную точку X⁽¹⁾, положить Y⁽¹⁾ = X⁽¹⁾, k = j = 1. При этом X^(k) - координаты минимальной точки на k-той итерации, Y^(j) - координаты точки на j-том шаге каждой итерации. Перейти к основному этапу.

Основной этап. Шаг 1. Если f(Y^(j) + l_j ) < f(Y^(j)), то шаг по j-му направлению считается “успешным”. Положить Y^(j+1) =Y^(j) + l_j и заменить l_j на al_j. Если же f(Y^(j) + l_j ) ³ f(Y_j), то шаг считается “неудачным”. Положить Y^(j+1) = Y^(j) и заменить l_j на bl_j. Если j < n, то заменить j на j + 1 и вернуться к шагу 1. В противном случае, т.е. при j = n перейти к шагу 2.

Шаг 2. Если f(Y⁽ⁿ⁺¹⁾) < f(Y⁽¹⁾), т. е. если хотя бы один спуск по направлению при шаге 1 оказался успешным, положить Y⁽¹⁾ = Y⁽ⁿ⁺¹⁾, j = 1 и повторить шаг 1. Пусть f(Y⁽ⁿ⁺¹⁾) = f(Y⁽¹⁾), т.е. каждый из n последних спусков по направлению на шаге 1 был неудачным. Если f(Y⁽ⁿ⁺¹⁾) < f(X^(k)), т.е. по крайней мере один удачный спуск встретился в течении k-й итерации на шаге 1, то перейти к шагу 3. Если f(Y⁽ⁿ⁺¹⁾) = f(X^(k)), т.е. не было не одного удачного спуска по направлению, то остановиться. При этом X^(k) является приближенным оптимальным решением, если |l_j| < eдля всех j. В противном случае положить Y⁽¹⁾ = Y⁽ⁿ⁺¹⁾, j = 1 и перейти к шагу 1.

Шаг 3. Положить X^(k+1) = Y⁽ⁿ⁺¹⁾. Если ||X^(k+1) - X^(k)|| < e, то остановиться; X^(k+1) - приближенное оптимальное решение. В противном случае вычислить l₁, …, l_n из соотношения построить новые направления, обозначить их через положить Y⁽¹⁾ = X^(k+1), заменить k на k + 1 положить j = 1 и перейти к шагу 1.

Дискретные шаги выбираются вдоль n направлений поиска на шаге 1. Если движение вдоль S_j оказалось успешным, то l_j заменяется на al_j, если же на этом направлении постигла неудача, то l_j заменяется на bl_j. Так как b< 0, то неудача приводит к сдвигу в обратном направлении вдоль j-го вектора на следующей реализации шага 1. Шаг 1 повторяется до тех пор, пока неудача будет иметь место при спуске по каждому направлению поиска. В этом случае строятся новые направления поиска.

Пример расчета экстремума функции методом Розенброка с дискретным шагом.

Постановка задачи. Минимизировать f(X) = (x₁ - 2)⁴ + (х₁ - 2х₂)² с точностью e=0,01. Эта функция имеет минимум в точке X^* = [2 1]^Т, где f(X) = 0. Выбираем начальное приближение X⁽¹⁾ = [2.5 2.5]^Т и параметры алгоритма: l₁ = l₂ = 0,5; a = 3; b= 0,5; направления начального поиска совпадают с координатными осями = [1 0]^Т, = [0 1]^Т.

Исследующий поиск.

Вычислим f(Y⁽²⁾) в точке 2

Y⁽²⁾ =

Здесь f(Y⁽²⁾) = 5,0, т.е. имеет место “удача”, поэтому шаг по х₁ увеличивается l₁ = 3×0,5 =1,5. Затем вычисляем f(Y⁽³⁾) в точке 3

Y⁽³⁾ =

Здесь f(Y⁽³⁾) = 10,0, т. е. “неудача”, поэтому шаг по х₂ уменьшается и направление изменяется на противоположное l₂ = -0,5×0,5 = -0,25.

При наличии одной “удачи” поиск продолжаем. Считаем Y⁽¹⁾ = Y⁽³⁾.

Вычисляем f(Y⁽²⁾) в точке 4

Y⁽²⁾ =

Здесь f(Y⁽²⁾)=39,31, что говорит о “неудаче”, поэтому величина шага уменьшается l₁ = -1,5×0,5 = -0,75.

Рассчитываем f(Y⁽³⁾) в точке 5

Y⁽³⁾ =

Здесь f(Y⁽⁵⁾) = 3,25. Следовательно, шаг является успешным, l₂ = 3×0,25 = 0,75

Поиск продолжается аналогичным образом до 9 точки. На этом первый исследующий поиск заканчивается, т. к. два последних расчета 8 и 9 неудачны. В качестве результата принимается координата [3 1,5] 7 точки, которая обозначается за X⁽²⁾ = Y⁽¹⁾.

Построение новых направлений поиска.Новое направление 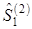совпадает с вектором перехода из X⁽¹⁾ в X⁽²⁾, а достраивается ортогонально к 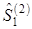. Рассчитаем единичные направления по формуле (2.5), а векторы а₁⁽¹⁾ и а₂⁽¹⁾ по формуле (2.6).

Определяем составляющие шага где перехода из X⁽¹⁾ = [2.5 2.5]^Т в X⁽²⁾ = [3 1,5]^Т. =3-2,5=0,5, =1,5-2,5=-1

Находим компоненты векторов

а₁⁽¹⁾ = 0,5× ; а₂⁽¹⁾ = -1× ;

Рассчитываем направления 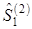и

=[0,45-0,89]^T

b₂⁽¹⁾= ;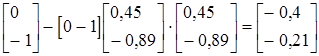

На этом завершена первая итерация метода. Точка с 10 по 13 соответствуют результатам исследующего поиска на второй итерации. После 16 итераций получается следующий результат: X^(*) = [1,99959 0,99979]; f(X^(*)) = 0,285×10^‑13, что указывает на высокую эффективность метода. Результаты расчетов двух итераций метода с использованием табличного процессора EXСEL представлены в таблице 2.3. Траектория поиска приведена на рис.2.3.

Таблица 2.3

Расчет минимума функции f(X) = (x₁ - 2)⁴ + (х₁ - 2х₂)² методом Розенброка.

1. Исследующий поиск
№	x1	x2	s1	s2	f(x)
	2.50	2.50			6.313
	3.00	2.50	0.50	0.00	5.000
	3.00	3.00	0.00	0.50	10.000
	4.50	2.50	1.50	0.00	39.313
	3.00	2.25	0.00	-0.25	3.250
	2.25	2.25	-0.75	0.00	5.066
	3.00	1.50	0.00	-0.75	1.000
	3.38	1.50	0.38	0.00	3.715
	3.00	-1.25	0.00	-2.25	31.250
1. Поворот осей
	x1	x2	||R||	f(x)
	3.00	1.50		1.000
λ	0.50	-1.00
a1	0.50	-1.00	1.118
a2	0.00	-1.00	1.000
b2	-0.4	-0.21	0.452
S1	0.45	-0.89
S2	-0.8854	-0.465
2. Исследующий поиск в новой системе координат
№	x1	x2	s1	s2	f(x)
	3.00	1.50			1.000
	3.22	1.05	0.22	-0.45	3.492
	2.56	1.27	-0.44	-0.23	0.097
	2.45	1.49	-0.11	0.22	0.328
	1.23	0.57	-1.33	-0.70	0.361

На второй итерации метода реализован исследующий поиск с помощью дискретных шагов в новой системе координат. Из таблицы видно, что на шаге 3 и 4 происходит «неудача». Поэтому оптимальной точкой исследующего поиска будет точка 2 [2.56; 1.27]. В этой точке опять производится поворот координатных осей, и процедура расчета повторяется.