 |
Главная |
Вычисление определенного интеграла методом замены переменной
|
из
5.00
|
При вычислении определенного интеграла методом замены переменной (способом подстановки) определенный интеграл  преобразуется с помощью подстановки
преобразуется с помощью подстановки 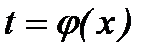 или
или 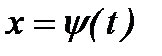 в определенный интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются соответственно новыми пределами t1 и t2, которые находятся из исходной подстановки.
в определенный интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются соответственно новыми пределами t1 и t2, которые находятся из исходной подстановки.
Из первой подстановки новые пределы интегрирования вычисляются непосредственно: 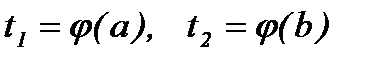 .
.
Из второй подстановки новые пределы интегрирования находятся путем решения уравнений 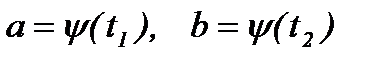 .
.
Таким образом, имеем
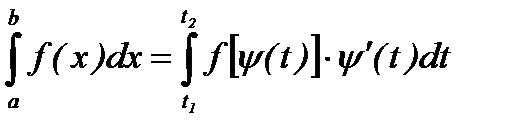
Пример 1: Вычислить определенный интеграл методом замены переменной 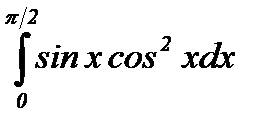
Решение: 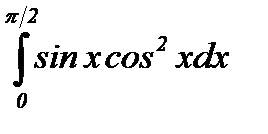 =
= 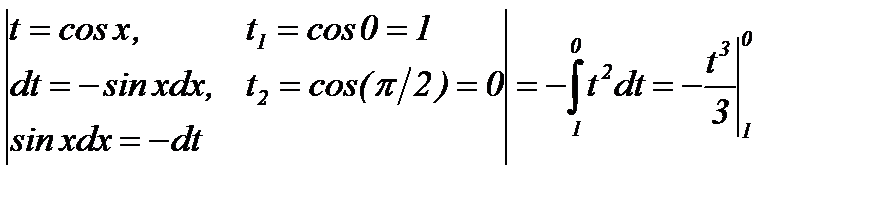
 .
.
Пример 2: Вычислить определенный интеграл: 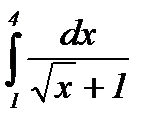 .
.
Решение: 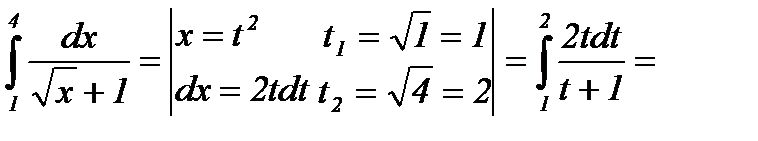
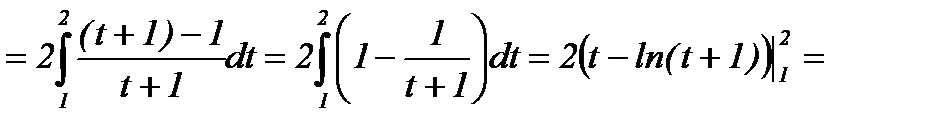
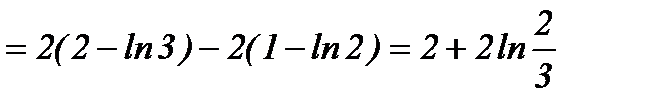 .
.
Вопросы для самопроверки по теме 3 Интегральное исчисление:
- В чем заключается смысл действия, обратного дифференцированию?
- Дать определение первообразной функции
- Чем отличаются друг от друга любые две первообразные данной функции
 ?
? - Как проверить, правильно ли найдена первообразная данной функции
 ?
? - Дать определение неопределенного интеграла.
- Перечислить свойства неопределенного интеграла
- Дать определение определенного интеграла.
- Перечислить свойства определенного интеграла.
- Запишите формулу Ньютона-Лейбница для вычисления определенного интеграла.
- В чем отличия методов замены переменной в определенном и неопределенном интегралах?
Варианты контрольных заданий
Вариант 1.
Задача 1. Найти производные следующих функций:
а) 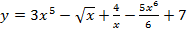 . Вычислить
. Вычислить 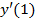
б) 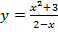
в) 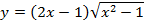
г) 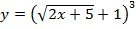
Задача 2. В какой момент времени скорость тела, движущегося по закону 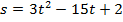 равна нулю.
равна нулю.
Задача 3. Найдите промежутки монотонности следующих функций
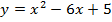
Задача 4. Исследуйте на экстремум следующие функции
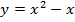
Задача 5. Найти следующие интегралы:
а) 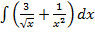
б) 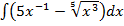
в) 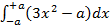
г) 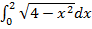
Задача 6. Фигура, ограниченная прямыми  и осью Оx, вращается вокруг оси абсцисс. Найти объем полученного тела вращения.
и осью Оx, вращается вокруг оси абсцисс. Найти объем полученного тела вращения.
Вариант 2
Задача 1. Найти производные следующих функций:
а) 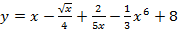 .
.
б) 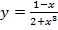 . Вычислить
. Вычислить 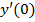
в) 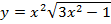
г) 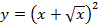
Задача 2. Построить график скорости движения тела, заданного уравнениями:
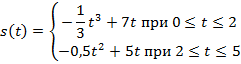
Задача 3. Найдите промежутки монотонности следующих функций
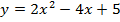
Задача 4. Исследуйте на экстремум следующие функции
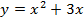
Задача 5. Найти следующие интегралы:
а) 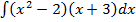
б) 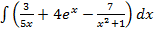
в) 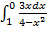
г) 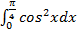
Задача 6. Найти объем тела, полученного вращением части кривой 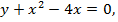 отсекаемой осью Оx от ее вершины, вокруг оси абсцисс.
отсекаемой осью Оx от ее вершины, вокруг оси абсцисс.
Вариант 3
Задача 1. Найти производные следующих функций:
а) 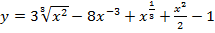 .
.
б) 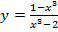
в) 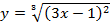 . Вычислить
. Вычислить 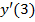
г) 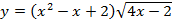
Задача 2. В какой момент времени скорость тела, движущегося по закону 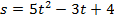 окажетсяравной 27 ед.
окажетсяравной 27 ед.
Задача 3. Найдите промежутки монотонности следующих функций
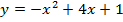
Задача 4. Исследуйте на экстремум следующие функции
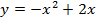
Задача 5. Найти следующие интегралы:
а) 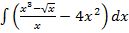
б) 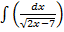
в) 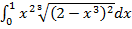
г) 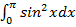
Задача 6. Фигура, ограниченная прямыми 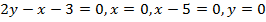 вращается вокруг оси абсцисс. Найти объем полученного тела вращения.
вращается вокруг оси абсцисс. Найти объем полученного тела вращения.
Вариант 4
Задача 1. Найти производные следующих функций:
а) 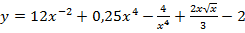 .
.
б) 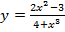 . Вычислить
. Вычислить 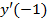
в). 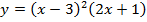
г) 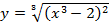
Задача 2.Найти уравнение касательной к кривой 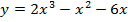 , проходящей через точку с абсциссой, равной -1
, проходящей через точку с абсциссой, равной -1
Задача 3. Найдите промежутки монотонности следующих функций
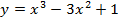
Задача 4. Исследуйте на экстремум следующие функции
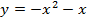
Задача 5. Найти следующие интегралы:
а) 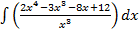
б) 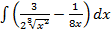
в) 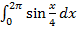
г) 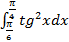
Задача 6. Фигура, образованная кривой 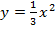 и прямыми
и прямыми 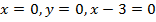 вращается вокруг оси абсцисс. Найти объем полученного тела вращения.
вращается вокруг оси абсцисс. Найти объем полученного тела вращения.
Вариант 5
Задача 1. Найти производные следующих функций:
а) 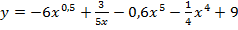 .
.
б) 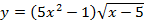
в). 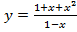 . Вычислить
. Вычислить 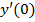
г) 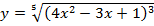
Задача 2.Тело движется прямолинейно по закону 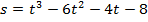 . Определить скорость тела в конце пятой секунды (
. Определить скорость тела в конце пятой секунды ( 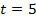 ). Путь
). Путь 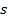 выражен в метрах
выражен в метрах
Задача 3. Найдите промежутки монотонности следующих функций
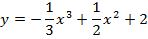
Задача 4. Исследуйте на экстремум следующие функции
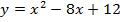
Задача 5. Найти следующие интегралы:
а) 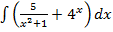
б) 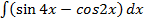
в) 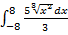
г) 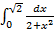
Задача 6. Фигура, ограниченная кривой 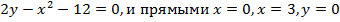 вращается вокруг оси абсцисс. Найти объем полученного тела вращения.
вращается вокруг оси абсцисс. Найти объем полученного тела вращения.
Вариант 6
Задача 1. Найти производные следующих функций:
а) 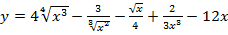 .
.
б) 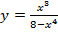 . Вычислить
. Вычислить 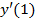
в). 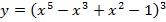
г) 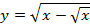
Задача 2.Найти уравнения касательных к кривой 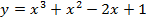 , образующих с осью абсцисс угол 135 градусов.
, образующих с осью абсцисс угол 135 градусов.
Задача 3. Найдите промежутки монотонности следующих функций
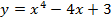
Задача 4. Исследуйте на экстремум следующие функции
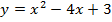
Задача 5. Найти следующие интегралы:
а) 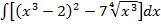
б) 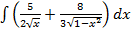
в) 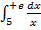
г) 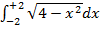
Задача 6. Найти объем тела, поверхность которого образуется вращением кривой 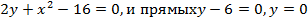 вокруг оси Oy.
вокруг оси Oy.
Вариант 7
Задача 1. Найти производные следующих функций:
а) 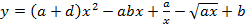 .
.
б) 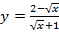 .
.
в) 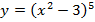 Вычислить
Вычислить 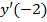
г) 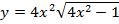 г)
г)
Задача 2. Построить график скорости движения тела, заданного уравнениями:
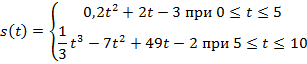
Задача 3. Найдите промежутки монотонности следующих функций,
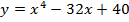
Задача 4. Исследуйте на экстремум следующие функции
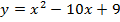
Задача 5. Найти следующие интегралы:
а) 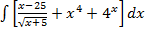
б) 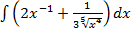
в) 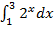
г) 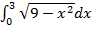
Задача 6. Найти площадь фигуры, ограниченной кривой 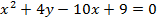 и прямой
и прямой 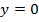
Вариант 8
Задача 1. Найти производные следующих функций:
а) 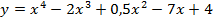 Вычислить
Вычислить 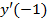
б) 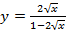 .
.
в). 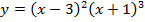
г) 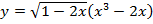
Задача 2.Найти уравнения касательных к кривой 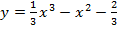 , параллельных оси Оx.
, параллельных оси Оx.
Задача 3. Найдите промежутки монотонности следующих функций
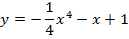
Задача 4. Исследуйте на экстремум следующие функции
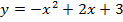
Задача 5. Найти следующие интегралы:
а) 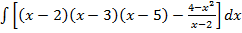
б) 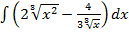
в) 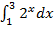
г) 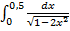
Задача 6. Шар, диаметр которого равен 12 см, рассечен тремя параллельными плоскостями, удаленными друг от друга на расстояния, равные четвертой части его диаметра. Определить объем вырезанного шарового слоя.
Вариант 9
Задача 1. Найти производные следующих функций:
а) 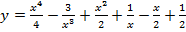 . Вычислить
. Вычислить 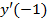
б) 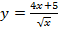 .
.
в) 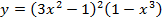 г)
г) 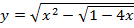 г)
г)
Задача 2. Построить график скорости движения тела, заданного уравнениями:
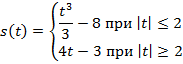
Задача 3. Найдите промежутки монотонности следующих функций
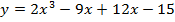
Задача 4. Исследуйте на экстремум следующие функции
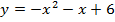
Задача 5. Найти следующие интегралы:
а) 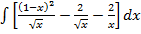
б) 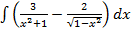
в) 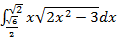
г) 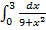
Задача 6. Найти объем шарового сегмента высотой 3 см, отсеченного от шара радиуса 6 см
Вариант 10
Задача 1. Найти производные следующих функций:
а) 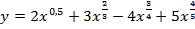
б) 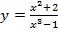 .
.
в). 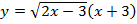 Вычислить
Вычислить 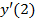
г) 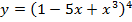
Задача 2. В каких точках кривой 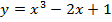 , надо провести касательную, чтобы она была параллельна прямой
, надо провести касательную, чтобы она была параллельна прямой 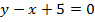
Задача 3. Найдите промежутки монотонности следующих функций
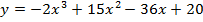
Задача 4. Исследуйте на экстремум следующие функции
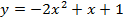
Задача 5. Найти следующие интегралы:
а) 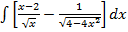
б) 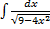
в) 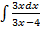
г) 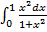
Задача 6. Найти объем тела, поверхность которого образуется вращением дуги окружности 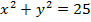 и прямых
и прямых 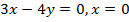 вокруг оси ОY
вокруг оси ОY
Вариант 11
Задача 1. Найти производные следующих функций:
а) 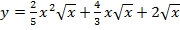
б) 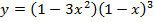 Вычислить
Вычислить 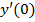
в). 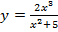 .
.
г) 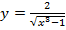
Задача 2.Построить график изменения скорости тела, движущегося по закону 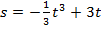 , на отрезке времени
, на отрезке времени 
Задача 3. Найдите промежутки монотонности следующих функций
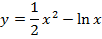
Задача 4. Исследуйте на экстремум следующие функции
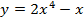
Задача 5. Найти следующие интегралы:
а) 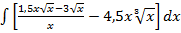
б) 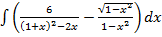
в) 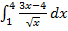
г) 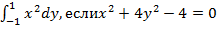
Задача 6. Вычислить объем тела, полученного при вращении вокруг оси OYфигуры, ограниченной прямыми 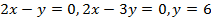
Вариант 12
Задача 1. Найти производные следующих функций:
а) 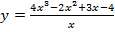 .
.
б) 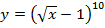 . Вычислить
. Вычислить 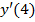
в) 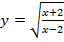
г) 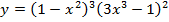
Задача 2. Построить график скорости движения тела, заданного уравнениями:
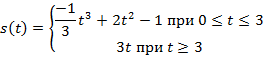
Задача 3. Найдите промежутки монотонности следующих функций
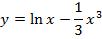
Задача 4. Исследуйте на экстремум следующие функции
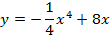
Задача 5. Найти следующие интегралы:
а) 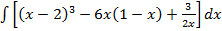
б) 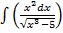
в) 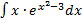
г) 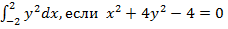
Задача 6. Площадь фигуры, ограниченной положительными полуосями координат и прямыми 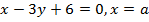 , равна 48 кв.ед. масшатаба. Определить a(верхний предел интеграла)
, равна 48 кв.ед. масшатаба. Определить a(верхний предел интеграла)
Вариант 13
Задача 1. Найти производные следующих функций:
а) 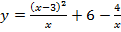 . Вычислить
. Вычислить 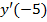
б) 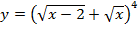
в). 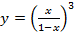 .
.
г) 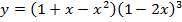
Задача 2. В каких точках кривой 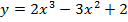 надо провести касательную, чтобы она была параллельна прямой
надо провести касательную, чтобы она была параллельна прямой 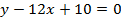
Задача 3. Найдите промежутки монотонности следующих функций
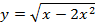
Задача 4. Исследуйте на экстремум следующие функции
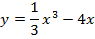
Задача 5. Найти следующие интегралы:
а) 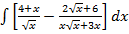
б) 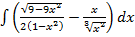
в) 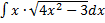
г) 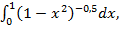
Задача 6. Найти объем параболоида, поверхность которого образована вращением дуги параболы 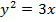 , заключенной между прямыми
, заключенной между прямыми 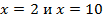 , вокруг оси Оx.
, вокруг оси Оx.
Вариант 14
Задача 1. Найти производные следующих функций:
а) 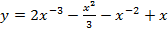
б) 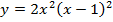 . Вычислить
. Вычислить 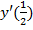
в). 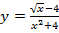
г) 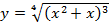
Задача 2. Найти уравнение касательной к кривой 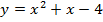 , параллельной прямой
, параллельной прямой
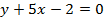 .
.
Задача 3. Найдите промежутки монотонности следующих функций
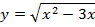
Задача 4. Исследуйте на экстремум следующие функции
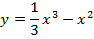
Задача 5. Найти следующие интегралы:
а) 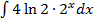
б) 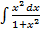
в) 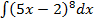
г) 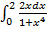
Задача 6. Найти площадь, ограниченную прямыми 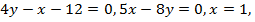
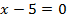 .
.
Вариант 15
Задача 1. Найти производные следующих функций:
а) 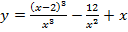
б) 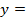 .
. 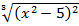
в). 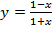 . Вычислить
. Вычислить 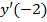
г) 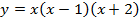
Задача 2. К кривой 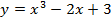 проведена касательная в точке
проведена касательная в точке 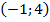 . Найти уравнение этой касательной.
. Найти уравнение этой касательной.
Задача 3. Найдите промежутки монотонности следующих функций
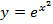
Задача 4. Исследуйте на экстремум следующие функции
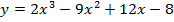
Задача 5. Найти следующие интегралы:
а) 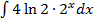
б) 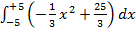
в) 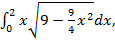
г) 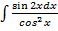
Задача 6. Фигура, ограниченная дугами парабол 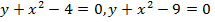 и осью абсцисс, вращается вокруг оси ординат. Найти объем полученного тела вращения
и осью абсцисс, вращается вокруг оси ординат. Найти объем полученного тела вращения
|
из
5.00
|
Обсуждение в статье: Вычисление определенного интеграла методом замены переменной |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

