Алгоритм метода покоординатного спуска

1. Задается точность вычисления 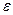, начальный шаг 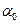, минимально допустимый шаг 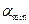, точка начального приближения 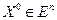, порядковый номер итерации k=0 и вычисляется .

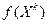2. Запоминаем .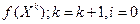

3. Начинаем поиск параллельно оси Ох_i : 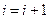,если 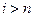, переходим к п. 11 , иначе к п. 4.

4. Задаем шаг .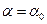

5. Задаем знак .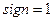

6. Вычисляем 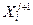в соответствии с формулой (1.6) и значение функции в новой точке.

7. Если новое значение функции меньше предыдущего, то принимаем 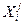как 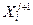, 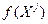запоминаем как 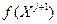и возвращаемся к п. 6, иначе меняем знак 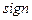на противоположный.

8. Если знак 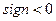,то переходим к п. 6, иначе к п. 9.

9. Уменьшим величину шага .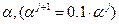

10. Если текущий шаг 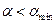, то переходим к п. 3, иначе к п. 5.

11. Проверка условия достижения заданной точности: 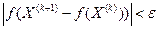и если оно выполняется, то переходим к п. 12, иначе к п. 2.

12. Завершить вычисления, приняв за точку минимума 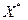последнее значение Х^k,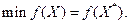

 

4. Текст программы.

 

Смотри приложение №1.

 

1. Метод деформируемого многогранника (метод Нелдера — Мида).

Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий градиентов функции, а поэтому легко применим к негладким и/или зашумлённым функциям.

В методе Нелдера и Мида минимизируется функция n независимых переменных с использованием n+1 вершин деформируемого многогранника в Eⁿ. Каждая вершина может быть идентифицирована вектором x. Вершина (точка) в Eⁿ, в которой значение f(x) максимально, проектируется через центр тяжести (центроид) оставшихся вершин. Улучшенные (более низкие) значения целевой функции находятся последовательной заменой точки с максимальным значением f(x) на более «хорошие точки», пока не будет найден минимум f(x).

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума. Предполагается, что серьёзных ограничений на область определения функции нет, то есть функция определена во всех встречающихся точках.

Параметрами метода являются:

· коэффициент отражения α > 0, обычно выбирается равным 1.

· коэффициент сжатия β > 0, обычно выбирается равным 0,5.

· коэффициент растяжения γ > 0, обычно выбирается равным 2.

 

Алгоритм метода.

Пусть 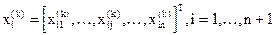, является i-й вершиной (точкой) в Eⁿ на k-м этапе поиска, k=0, 1, …, и пусть значение целевой функции в x^(k)_i равно f(x^(k)_i). Кроме того, отметим те векторы x многогранника, которые дают максимальное и минимальное значения f(x).

 

Определим

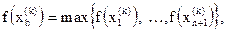
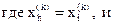
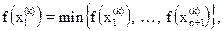
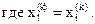Поскольку многогранник в Eⁿ состоит из (n+1) вершин x₁, …,x_n+1, пусть x_n+2 будет центром тяжести всех вершин, исключая x_h.

 

Тогда координаты этого центра определяются формулой

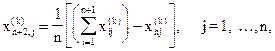(1.7)

где индекс j обозначает координатное направление.

 

Начальный многогранник обычно выбирается в виде регулярного симплекса (но это не обязательно) с точкой 1 в качестве начала координат; можно начало координат поместить в центр тяжести. Процедура отыскания вершины в Eⁿ, в которой f(x) имеет лучшее значение, состоит из следующих операций:

 

1. Отражение – проектирование через центр тяжести в соответствии с соотношением
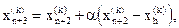(1.8)
где a>0 является коэффициентом отражения; 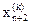– центр тяжести, вычисляемый по формуле (1); 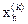– вершина, в которой функция f(x) принимает наибольшее из n+1 значений на k-м этапе.

 

2. Растяжение. Эта операция заключается в следующем: если 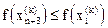, то вектор 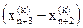растягивается в соответствии с соотношением
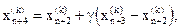(1.9)
где g>1 представляет собой коэффициент растяжения. Если 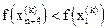, то 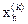заменяется на 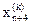и процедура продолжается снова с операции 1 при k=k+1. В противном случае 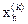заменяется на 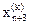и также осуществляется переход к операции 1 при k=k+1.

 

3. Сжатие. Если 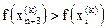для всех i¹h, то вектор 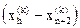сжимается в соответствии с формулой
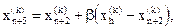(1.10)
где 0<b<1 представляет собой коэффициент сжатия. Затем 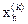заменяем на 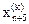и возвращаемся к операции 1 для продолжения поиска на (k+1)-м шаге.

 

4. Редукция. Если 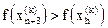, все векторы 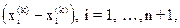уменьшаются в 2 раза с отсчётом от 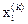в соответствии с формулой
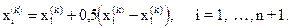(1.11)

Затем возвращаемся к операции 1 для продолжения поиска на (k+1)-м шаге.

 

 

Критерий окончания поиска, использованный Нелдером и Мидом, состоял в проверке условия

 

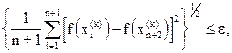(1.12)

 

где e – произвольное малое число, а 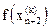– значение целевой функции в центре тяжести .

 

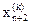На рис.2 приведена блок-схема поиска методом деформируемого многогранника

 

Пуск

 

Вычислить начальные значения

x_i⁽⁰⁾, i = 1, 2, …, n+1, и f(x⁽⁰⁾)

начального симплекса

 

Вычислить x_h и x_l и c

 

Отражение: вычислить

x_n+3 = x_n+2 + a(x_n+2 - x_n)

 

Вычислить

f(x_n+3)

 

Нет

Выполняется ли

неравенство

f(x_n+3) < f(x_h) ?

		Да

 

 

Растяжение: вычислить

x_n+4 = x_n+2 + g(x_n+3 - x_n+2)

 

 

Вычислить f(x_n+4)

 

Выполняется ли

неравенство

f(x_n+4) < f(x_l) ?

 

 

Заменить

x_h на x_n+4

 

		Нет

Выполняется ли

неравенство f(x_n+3) < f(x_i)

для всех i ¹ h ?

			Нет
		Нет
	Да
		Нет

 

 

Заменить

x_h на x_n+3

 

		Нет

 

 

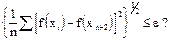
Рис. 2
Выполняется ли

неравенство

f(x_n+3) < f(x_h) ?

	Да
		Да

 

 

Заменить

x_h на x_n+3

 

Сжатие: вычислить

x_n+5 = x_n+2 + b(x_h - x_n+2)

 

 

Вычислить f(x_n+5)

 

Выполняется ли

неравенство

f(x_n+5) > f(x_h) ?

 

 

Заменить

Да

x_h на x_n+5

 

Редукция: заменить

все x_i на x_l + ¹/₂(x_i - x_l)

	Да

 

Останов

7. Текст программы.

 

Смотри приложение №1.

 

Задание.

Используя метод покоординатного спуска или метод деформированного многогранника, реализовав их в виде программ на Turbo Pascal, найти минимум следующих функций:

 

1) f(X)=x₁²+ x₂² +x₃²+ x₁–x₁ *x₂-2x₃

2) f(X)=100( x₂ –x₁²) ²+ (1-x₁)²

3) f(X)=( x₂ –x₁²) ²+ (1-x_1*x₂)²

4) f(X)=5x₁²+ x₂² + 4x₁ *x₂-16x₁-12x₂

5) f(X= х₁² + 4х₂² –4х₁ –8х₂ + 5

 

 

 

 

Лабораторная работа №2.