Метод решения задачи на быстродействие с учетом демпфирования

 

Рассмотрим систему, динамика которой описывается следующей системой дифференциальных уравнений

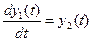
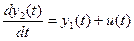(6.4)

 

Такими уравнениями, например, описывается движение маятника в поле массовых сил при действии управляющей силы u(t).

Требуется перевести систему (6.4) из состояния

в начало координат ( y_1к=0, y_2к=0) за минимальное время.

В данном случае

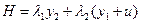
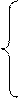где

Соответственно,

 

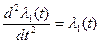
Решая последнюю систему уравнений, найдем

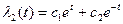
Будем считать, что на управление наложены ограничения (│u(t) │≤1).

Из условия максимума функции H следует, что

.

Учитывая, что - функция, имеющая не более одного нуля, т.е. меняющая знак не более одного раза, оптимальное управление может быть: или с одним переключением.

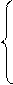Предположим, что , тогда система (6.4) запишется в следующем виде:

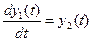
Отсюда следует, что (у₁+1)dy₁=y₂dy₂ . Интегрируя, получим уравнение фазовой траектории: (у₁+1)²-у₂²=R₁.

Этим уравнением описывается семейство гипербол с центром в т.(-1;0) , представленное на рис.6. Т.к. , то движение будет слева направо в верхней полуплоскости (у₂>0) и справа налево в нижней. Как и ранее, нас интересуют дуги тех гипербол, которые приводят в начало координат. Это дуга АО.

И только при R₁=1 фазовая траектория проходит через начало координат. Поэтому с управлением 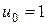можно попасть в начало координат только, стартуя с фазовой траектории АО.

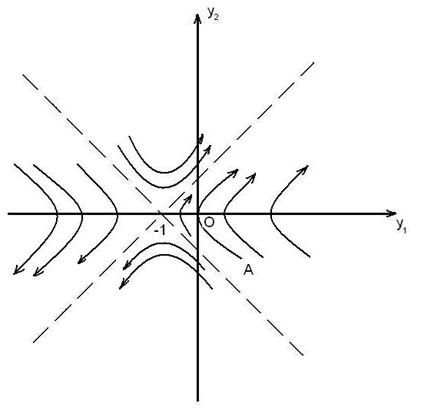
Рис.6

 

Аналогично, при управлении ,получим: (у₁-1)²-у₂²=R₂. Этим уравнением описывается семейство гипербол с центром в т.(1;0) , представленное на рис.7. Соответственно, с управлением можно попасть в начало координат только, стартуя с фазовой траектории BО, которая соответствует значению R₂=1.

 

Рис.7

В результате получим следующее: данная задача имеет решение не во всех случаях, в отличии от предыдущей задачи быстродействия. Требуется, чтобы начальное состояние системы (6.4) входило в область управляемости, представленную на рис. 8 в виде областей C и D. Из других областей привести систему в начало координат невозможно.

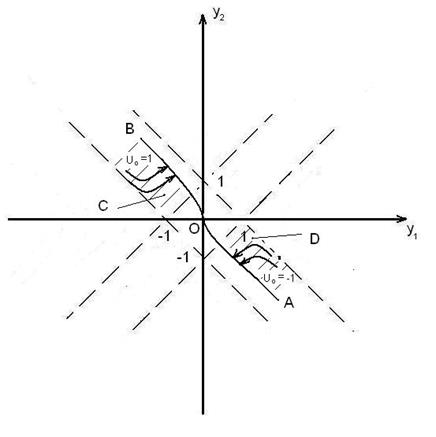
Рис.8

Соответственно, управление формируется следующим образом:

u₀(у₁, у₂)=1, если (у₁, у₂) 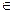С или находится на дуге АО;

u₀(у₁, у₂)=-1, если (у₁, у₂) 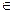D или находится на дуге ВО.

Если начальное состояние системы (6.4) соответствует дуге АО или ВО, то управление остается постоянным, и наша система придет в начало координат. В случае, когда начальное состояние системы (6.4) входит в область управляемости, но не находится на дугах АО или ВО важно правильно выбрать момент переключения управления. Критерием выбора будет сравнение значения у₁(t) c константами R₁ или R₂.

Предположим, что начальному состоянию системы соответствует точка М на фазовой плоскости с координатами (у₁₀,у₂₀) и для определенности она принадлежит области С. Тогда u₀(у₁₀, у₂₀)=1 и (у₁₀+1)²-у₂₀²=R₁ . Двигаясь по этой траектории, т. М обязательно окажется на дуге ВО. Значит, будет существовать решение следующей системы уравнений:

(у₁(t)+1)²-у₂(t)²=R₁

(у₁(t)-1)²-у₂(t)²=1

 

Решая ее получим, что смена управления произойдет когда у₁(t) приметзначение и дальше т. М будет двигаться по дуге ВО.

Аналогично, если изначально точка М находилась в области D, то момент переключения управления с u₀(у₁, у₂)=-1 на u₀(у₁, у₂)=1, т.е. движение по дуге АО, произойдет при у₁(t)= .

6. Алгоритм решения задачи на быстродействие с учетом демпфирования .

1. Задаем исходные данные: шаг интегрирования, шаг вывода результатов, начальную точку на фазовой плоскости Точка у₀ должна принадлежать области управляемости. В зависимости от 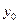выбирается управление u₀ и вычисляется константа R₁ или R₂.

2. Интегрируем численным методом Рунге-Кутта дифференциальные уравнения (6.4).При этом, контролируя текущее значения у₁(t) , меняем не более одного раза управление u_0..

3. При попадании с точностью 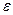в начало координат, прекращаем интегрирование.

В результате получаем искомое время , за которое система переводится из произвольного начального состояния в заданное конечное.

Примечание. Если конечным состоянием является не начало координат, т.е. у₁₁ =у_1к≠0, у₂₁=у_2к≠0, то выбираем новую систему координат, в которой . Соответственно требуется пересчитать и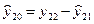

7. Текст программы.

Смотри приложение №6.

Задание.

1. Студентам требуется, используя данный в приложение №6 текст программы, самостоятельно подобрать исходные данные для решения задачи быстродействия: шаг интегрирования, шаг вывода результатов, y₀, u₀. При задании неправильных значений

y₀, u_{0, ,}находящихся вне области сходимости, задача не будет решена.

2. Получив решения обеих задач быстродействия, проанализировать полученные результаты. Сделать выводы по результатам работы.

 

ПРИЛОЖЕНИЕ

 

Приложение №1.

Текст программы на Turbo Pascal, в которой реализован метод покоординатного спуска

Uses Graph,Crt;

Type Vector=array[1..10] of real;

Var i,j,n,x0,y0,z:integer;

it:longint;

fx,f0,fxn,norm,h,h0,hmin,eps,m:real;

x,xn,Grad:Vector;

{================================================================}

{* Функция F(x) *}

Function f(x:Vector):real; { Eps=1e-3 }

Begin

{ Test !!! }

F:=sqr(x[1]+5.6)+sqr(x[2]-2.4) { 2 итерации }

 

{ 1 f:= sqr(x[1])+sqr(x[2])+sqr(x[3])+x[1]-x[1]*x[2]-2*x[3] }

{ 2 f:=100*sqr(x[2]-x[1]*x[1])+sqr(1-x[1]) }

{ 3 f:=sqr(x[2]-x[1]*x[1])+sqr(1-x[1]*x[2]) }

{ 4 f:= 5*sqr(x[1])+sqr(x[2])+4*x[1]*x[2]-16*x[1]-12*x[2] }

{ 5 f:= sqr(x[1])+2*sqr(x[2])+3*sqr(x[3])+10*x[1]-6*x[1]*x[3]-20*x[3] }

End;

 

 

{* Процедура инициализации графики *}

Procedure Gr(x,y:real);

Var gd,gm:integer;

Begin

gd:=detect;

initgraph(gd,gm,' ');

SetBkColor(15);

 

x0:=320;y0:=240;

SetColor(14);

Line(0,y0,640,y0);Line(x0,0,x0,480);

SetColor(2);

MoveTo(round(x0+x*m),round(y0-y*m))

End;

 

{* Процедура вывода графиков *}

Procedure Gr_out(x,y:real);

Begin

LineTo(round(x0+x*m),round(y0-y*m));

End;

 

procedure poisk;

begin

xn[i]:=x[i]+z*h; fxn:=f(xn);

end;

 

{================================================================}

Begin

h0:=1; { Шаг }

eps:=1e-3; { Точность }

hmin:=1e-4;

it:=0; { Количество итераций }

m:=10; { Масштаб }

 

Write('n='); Read(n); { Размерность }

for i:=1 to n do

x[i]:=10; { Начальная точкa }

 

Assign(Output,'grad.txt');

Rewrite(Output);

 

Gr(x[1],x[2]);

 

xn:=x; fx:=f(x); z:=1;

 

REPEAT

it:=it+1;

f0:=fx;

for i:=1 to n do begin

h:=h0;

Repeat

z:=1;

 

(* 1 *) repeat

poisk;

while fxn<fx do begin

x[i]:=xn[i]; fx:=fxn; poisk;

end;

z:=-z;

until z>0 (* 1 *);

 

h:=h/10;

Until h<hmin;

 

xn[i]:=x[i];

If (it>=10000)and(it<35500)or(it<=1000) Then

begin

Write('it=',it:4);

for j:=1 to n do

Write(' x[',j,']=',x[j]:10:6);

Writeln; end;

 

 

Gr_out(x[1],x[2]); {* Рисование графика *}

 

end; { for }

 

 

Until Abs(fx-f0)<Eps;

Writeln;

Write('it=',it:4);

for i:=1 to n do

Write(' x[',i,']=',x[i]:10:6);

Writeln;

 

 

ReadKey;

End.

 

Текст программы на Turbo Pascal, в которой реализован метод деформированного многогранника

 

Program SimplexMethod;

 

Uses Crt;

 

Type

TFloat = Real;

 

Const

N_S = 10;

Max_Float = 1.0e+32;

 

Type

Vector = Array[1..Succ(N_S)] Of TFloat;

Matrix = Array[1..Succ(N_S), 1..N_S] Of TFloat;

OptimFunc = Function(N: Byte; X: Vector): TFloat;

 

Var

X: Vector;

H, Fmin: TFloat;

N, I, IT : Integer;

Function OFunc(N: Byte; X: Vector): TFloat; Far;

Begin

OFunc:=100*sqr(X[2]-sqr(X[1]))+sqr(1-X[1]);

End;

 

 

Procedure Simplex(N: Byte; OFunc: OptimFunc; Eps, H: TFloat;

var X: Vector; var Fmin: TFloat; var IT: Integer);

Var

I, J, K, Ih, Ig, IL, ITR : Integer;

Smplx: Matrix;

Xh, Xo, Xg, Xl, Xr,Xc, Xe, F : Vector;

Fh, Fl, Fg, Fo, Fr, Fe: TFloat;

S, D, Fc: TFloat;

 

Const

Alpha = 1.0;

Betta = 0.5;

Gamma = 2.0;

 

Begin

For i:=1 To N Do Smplx[1,i] := X[i];

 

For i:=2 To Succ(N) Do

For j:=1 To N Do

If j = pred(i) Then Smplx[i,j]:=Smplx[1,j] + H

Else Smplx[i,j]:=Smplx[1,j];

 

For i:=1 To Succ(N) Do Begin

For j:=1 To N Do X[j]:=Smplx[i,j];

F[i]:=OFunc(N, X);

End;

 

Eps:=Abs(Eps); ITR:=0;

 

Repeat

 

Fh:=-Max_Float; Fl:=Max_Float;

For i:=1 To Succ(N) Do Begin

If F[i]>Fh Then Begin Fh:=F[i]; Ih:=i End;

If F[i]<Fl Then Begin Fl:=F[i]; IL:=i End;

End;

 

Fg:=-Max_Float;

For i:=1 To Succ(N) Do

If (F[i]>Fg)and(i<>Ih) Then Begin Fg:=F[i]; Ig:=i End;

 

For j:=1 To N Do Begin

Xo[j]:=0;

For i:=1 To Succ(N) Do If i<>Ih Then Xo[j]:=Xo[j]+Smplx[i,j];

Xo[j]:=Xo[j]/N;

Xh[j]:=Smplx[Ih,j];

Xl[j]:=Smplx[IL,j];

Xg[j]:=Smplx[Ig,j];

End;

Fo:=OFunc(N, Xo);

 

{Отражение- Alpha}

For j:=1 To N Do Xr[j]:=Xo[j] + Alpha*(Xo[j]-Xh[j]);

Fr:=OFunc(N, Xr);

 

If Fr<Fl Then Begin

 

{Pастяжение- Gamma}

For j:=1 To N Do Xe[j]:=Gamma*Xr[j] + (1-Gamma)*Xo[j];

Fe:=OFunc(N, Xe);

If Fe<Fl Then Begin

For j:=1 To N Do Smplx[Ih,j]:=Xe[j]; F[Ih]:=Fe

End

Else Begin

For j:=1 To N Do Smplx[Ih,j]:=Xr[j]; F[Ih]:=Fr

End

End

Else

If Fr>Fg Then Begin

If Fr<=Fh Then Begin

For j:=1 To N Do Xh[j]:=Xr[j]; F[Ih]:=Fr

End;

 

{Cжатие- Betta}

For j:=1 To N Do Xc[j]:=Betta*Xh[j] + (1-Betta)*Xo[j];

Fc:=OFunc(N, Xc);

If Fc>Fh Then Begin

For i:=1 To Succ(N) Do Begin

 

{Редукция}

 

For j:=1 To N Do Begin

Smplx[i,j]:=0.5*(Smplx[i,j] + Xl[j]);

X[j]:=Smplx[i,j]

End;

F[i]:=OFunc(N, X);

End

End

Else Begin

For j:=1 To N Do Smplx[Ih,j]:=Xc[j]; F[Ih]:=Fc

End

End

Else Begin

For j:=1 To N Do Smplx[Ih,j]:=Xr[j]; F[Ih]:=Fr

End;

 

{Проверка}

S:=0; D:=0;

For i:=1 To Succ(N) Do Begin S:=S + F[i]; D:=D + Sqr(F[i]) End;

S:=Sqrt(Abs((D - Sqr(S)/Succ(N))/Succ(N)));

Inc(Itr);

Until (S<=Eps) or (It<ITR);

 

If Itr>IT Then IT:=-Itr Else IT:=Itr;

X:=XL;

Fmin:=F[IL];

End;

 

BEGIN

ClrScr;

WriteLn('Programma Realizacii Algoritm "Neldera-Mida"');

Write('Vvedite realnuju razmernoct vectora X: '); Read(N);

WriteLn('Vvedite nachalnoe Pribligenie vectora X: ');

For i:=1 to N do begin

Write( 'X[',i,']='); Read(X[i]);

end;

WriteLn('Zadaite GELAEMOE Kolichestvo Iteracii:'); ReadLn(IT);

 

Simplex(N, OFunc, 1.0e-8, 0.5, X, Fmin, It);

 

WriteLn('Vicheslennioe znachenie optimizacii:');

For i:=1 to N do WriteLn( 'X[',i,']=',X[i]);

 

WriteLn('Naidennii min Funkcii=',Fmin);

WriteLn('Zatrachennoe Chislo Iteraciy= ',It);

ReadLn;

END.

 

 

Приложение №2.

Текст программы на Turbo Pascal, в которой реализован градиентный метод

Uses Crt;

Type Vector=array[1..10] of real;

const eps=1e-3;

Var

i,n:integer;

it:longint;

fx,fxn,norm,h,m:real;

x,xn,Grad:Vector;

{================================================================}

{* Функция F(x) *}

Function f(x:Vector):real;

Begin

{ Test !!! }

{ Test !!! }

F:=sqr(x[1]+5.6)+sqr(x[2]-2.4) { 12 итераций }

 

{ 1 f:= sqr(x[1])+sqr(x[2])+sqr(x[3])+x[1]-x[1]*x[2]-2*x[3] }

{ 2 f:=100*sqr(x[2]-x[1]*x[1])+sqr(1-x[1]) }

{ 3 f:=sqr(x[2]-x[1]*x[1])+sqr(1-x[1]*x[2]) }

{ 4 f:= 5*sqr(x[1])+sqr(x[2])+4*x[1]*x[2]-16*x[1]-12*x[2] }

{ 5 f:= sqr(x[1])+2*sqr(x[2])+3*sqr(x[3])+10*x[1]-6*x[1]*x[3]-20*x[3] }

End;

 

 

{Вычисление градиента}

procedure rasch_grad;

const dx=1e-6;

begin

fx:=f(x);

 

for i:=1 to n do begin

x[i]:=x[i]+dx;

grad[i]:=(f(x)-fx)/dx;

x[i]:=x[i]-dx;

end;

end;

 

{Вычисление нормы }

function norma(grad:vector):real;

var S:real;

begin

S:=0;

for i:=1 to n do S:=S+sqr(grad[i]);

norma:=sqrt(S);

 

end;

 

 

{================================================================}

Begin

h:=1; {шаг}

it:=0; {количество итераций}

Write('n='); Read(n); { размерность }

for i:=1 to n do

x[i]:=10; { начальная точкa }

 

fx:=f(x); rasch_grad; norm:=norma(grad);

 

Assign(Output,'grad.txt');

Rewrite(Output);

 

while (norm>eps)and(h>eps/1e+9)do

 

begin

 

for i:=1 to n do xn[i]:=x[i]-h*grad[i]/norm;

fxn:=f(xn);

if fxn<fx then begin (*попытка удачна*)

it:=it+1; h:=1.25*h; x:=xn;

fx:=f(x); rasch_grad; norm:=norma(grad);

 

If (it>=10000)and(it<35500)or(it<=1000) Then

begin

Write('it=',it:4);

for i:=1 to n do

Write(' x[',i,']=',x[i]:10:6);

Writeln; end;

end

 

else h:=h/2; (*нeyдaчнaя попытка *)

 

end;

Writeln;

Write('it=',it:4);

for i:=1 to n do Write(' x[',i,']=',x[i]:10:6);

Writeln; Writeln(' f(x)=',fx);

;

NoSound;

 

ReadKey;

End.

Текст программы на Turbo Pascal, в которой реализован метод наискорейшего спуска

program SpeedSpusc;

Uses Graph,Crt;

Type Vector=array[1..10] of real;

Var i,n,k,x0,y0:integer;

it:longint;

fx,fxn,norm,h,h0,hmin,eps,m:real;

x00,x,xn,Grad,dx:Vector;

{================================================================}

{* Функция F(x) *}

Function f(x:Vector):real; { Eps=1e-3 }

Begin

{ Test !!! }

F:=sqr(x[1]+5.6)+sqr(x[2]-2.4) { 2 итерации }

 

{ 1 f:= sqr(x[1])+sqr(x[2])+sqr(x[3])+x[1]-x[1]*x[2]-2*x[3] }

{ 2 f:=100*sqr(x[2]-x[1]*x[1])+sqr(1-x[1]) }

{ 3 f:=sqr(x[2]-x[1]*x[1])+sqr(1-x[1]*x[2]) }

{ 4 f:= 5*sqr(x[1])+sqr(x[2])+4*x[1]*x[2]-16*x[1]-12*x[2] }

{ 5 f:= sqr(x[1])+2*sqr(x[2])+3*sqr(x[3])+10*x[1]-6*x[1]*x[3]-20*x[3] }

End;

 

{Вычисление градиента}

procedure rasch_grad;

const dx=1e-6;

begin

fx:=f(x);

for i:=1 to n do begin

x[i]:=x[i]+dx;

grad[i]:=(f(x)-fx)/dx;

x[i]:=x[i]-dx;

end;

end;

 

{Вычисление нормы для окончания расчетов}

function norma(grad:vector):real;

var S:real;

begin

S:=0;

for i:=1 to n do S:=S+sqr(grad[i]);

norma:=sqrt(S);

 

end;

 

 

{* Процедура инициализации графики *}

Procedure Gr(x,y:real);

Var gd,gm:integer;

Begin

gd:=detect;

initgraph(gd,gm,'c:\tp\bgi');

SetBkColor(15);

 

x0:=320;y0:=240;

SetColor(14);

Line(0,y0,640,y0);Line(x0,0,x0,480);

SetColor(2);

MoveTo(round(x0+x*m),round(y0-y*m))

End;

 

{* Процедура вывода графиков *}

Procedure Gr_out(x,y:real);

Begin

LineTo(round(x0+x*m),round(y0-y*m));

End;

 

 

{================================================================}

Begin

h0:=1; { Шаг }

hmin:=1e-4; { Шаг min }

eps:=1e-3; { Точность }

Write('n='); Read(n); { Размерность }

for i:=1 to n do

x[i]:=10; { Начальная точкa }

it:=0; { Количество итераций }

m:=10; { Масштаб }

 

Assign(Output,'grad.txt');

Rewrite(Output);

 

Gr(x[1],x[2]);

 

Repeat

fx:=f(x); rasch_grad; norm:=norma(grad);

h:=h0; x00:=x;

it:=it+1;

 

Repeat

for i:=1 to n do xn[i]:=x[i]-h*grad[i]/norm;

fxn:=f(xn);

if fxn<fx then begin

x:=xn;

fx:=fxn;

end

 

else begin

{ k:=k+1;

if k mod 2<>0 then h:=h/10 else h:=-h;

} h:=-h/10; end

Until (abs(h)<hmin);

 

for i:=1 to n do dx[i]:=x[i]-x00[i];

norm:=norma(dx);

 

If (it>=10000)and(it<36500)or(it<100) Then

begin

Write('it=',it:4);

for i:=1 to n do

Write(' x[',i,']=',x[i]:10:6);

Writeln; end; Gr_out(x[1],x[2]); {* Рисование графика *}

 

 

Until Norma(dx)<Eps;

Writeln;

Write('it=',it:4);

for i:=1 to n do Write(' x[',i,']=',x[i]:10:6);

Writeln; Writeln(' f(x)=',fx);

 

 

ReadKey;

End.

 

function norma(x:vec):real;

var

nG:real;

i:byte;

begin

nG:=0;

for i:=1 to n do

nG:=nG+sqr(x[i]);

 

norma:=sqrt(nG);

end;

 

BEGIN

iter:=0; h0:=1; h:=1; beta:=0.01;

Write(' введи количество неизвестных:'); Read(n);

Write(' введи количество ограничений в форме равенств:'); Read(m);

Write(' введи количество ограничений в форме неравенств:'); Read(p);

 

for i:=1 to n do

x[i]:=10; { Начальная точкa }

 

Repeat

 

x0:=x; h:=h0; iter:=iter+1; k:=0;

zx:=z(x);gradient ;norm:=norma(grad);

 

while (norm>eps) and (h>eps/1e9) do

begin

for i:=1 to n do

x1[i]:=x[i]-h*grad[i]/norm;

zx1:=z(x1);

if zx1<zx then begin

x:=x1; zx:=zx1 ; gradient;

norm:=norma(grad);

h:=1.25*h; k:=k+1;

end

else h:=h/2;

end;

 

for i:=1 to n do

Dx[i]:=x[i]-x0[i];

 

write(beta:10:1);

for i:=1 to n do

write(x[i]:10:6 );

writeln(' z(x)=',z(x),' k=',k);

 

beta:=10*beta;

until norma(Dx)<eps;

 

writeln('число итераций=',iter, ' при заданной точности ',eps:1:9);

END.

 

 

.

 

 

Приложение №4.