Построение линейной модели парной регрессии

ПРАКТИКУМ ПО КУРСУ « ЭКОНОМЕТРИКА»

Руководство составлено на основании учебной программы данной дисциплины, составленной в соответствии с государственными требованиями к минимуму содержания и уровню подготовки студентов экономических специальностей.

Содержание

Перечень тем и подтем

Тема 1.Парная регрессия и корреляция

Тема 2.Множественная регрессия и корреляция

Тема 3.Системы эконометрических уравнений

Тема 4.Временные ряды

Литература

Перечень тем

Тема 1. Парная регрессия и корреляция

1. Предварительно ознакомиться с теоретическим материалом:

Л1 [Гл. 2], Л2 [Гл. 1], Л3 [Гл. 1, 3, 5].

Примеры с решениями.

Пример 1.По территориям региона приводятся данные за календарный год (см. табл. 1).

Таблица 1

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	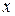Среднедневная Заработная плата, руб.,

Требуется:

1.Построить линейное уравнение парной регрессии от .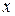

2.Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.

3.Оценить статистическую значимость параметров регрессии и корреляции с помощью -критерия Фишера и 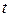-критерия Стьюдента.

4.Выполнить прогноз заработной платы при прогнозном значении среднедушевого прожиточного минимума 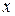, составляющем 107% от среднего уровня.

5.Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

6.На одном графике построить исходные данные и теоретическую прямую.

Решение:

1.Для расчета параметров уравнения линейной регрессии строим расчетную таблицу 2.

;

.

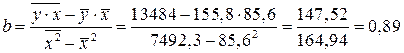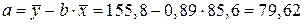Получим уравнение регрессии: .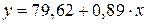

С увеличением среднедушевого прожиточного минимума на 100 руб. среднедневная заработная плата возрастает в среднем на 89 руб.

2.Тесноту линейной связи оценит коэффициент корреляции:

;

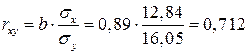Коэффициент детерминации при этом составит:

.

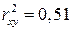Это означает, что 51% вариации заработной платы ( ) объясняется вариацией фактора 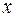– среднедушевого прожиточного минимума.

Качество модели определяет средняя ошибка аппроксимации:

.

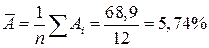Качество построенной модели оценивается как хорошее, так как не превышает 8-10%.

3.Оценку значимости уравнения регрессии в целом проведем с помощью -критерия Фишера. Фактическое значение -критерия:

.

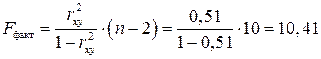Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы и 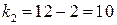составляет . Так как 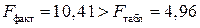, то уравнение регрессии признается статистически значимым.

Оценку статистической значимости параметров регрессии проведем с помощью 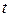-статистики Стьюдента и путем расчета доверительного интервала каждого из показателей.

Табличное значение 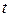-критерия для числа степеней свободы 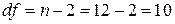и составит .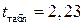

Определим случайные ошибки , , :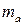

 

 

 

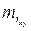Таблица 2

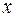
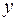
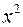
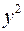
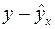
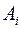
							‑16	12,0
							‑4	2,7
							‑23	17,2
								2,6
								1,9
								10,8
								0,0
								0,0
								5,3
								3,1
								7,5
							‑10	5,8
Итого								68,9
Среднее значение	85,6	155,8	13484,0	7492,3	24531,4	–	–	5,7
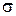
	12,84	16,05	–	–	–	–	–	–
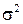
	164,94	257,76	–	–	–	–	–	–

;

;

.

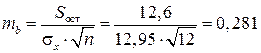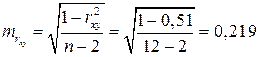Тогда

;

;

.

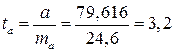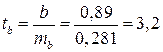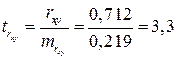Фактические значения 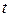-статистики превосходят табличное значение:

; ; ,

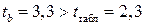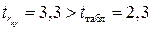поэтому параметры , 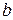и 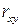не случайно отличаются от нуля, а статистически значимы.

Рассчитаем доверительные интервалы для параметров регрессии и 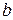. Для этого определим предельную ошибку для каждого показателя:

;

.

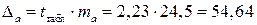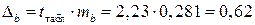Доверительные интервалы

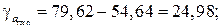
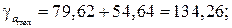
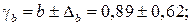
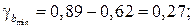
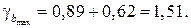
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры и 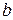, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.

4.Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит: 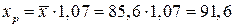руб., тогда прогнозное значение заработной платы составит: руб.

5.Ошибка прогноза составит:

.

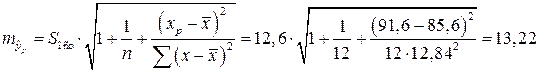Предельная ошибка прогноза, которая в 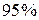случаев не будет превышена, составит:

.

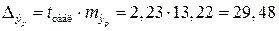Доверительный интервал прогноза:

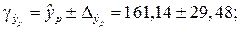
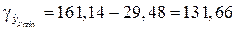руб.;

руб.

Выполненный прогноз среднемесячной заработной платы является надежным ( 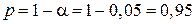) и находится в пределах от 131,66 руб. до 190,62 руб.

6.Построим на одном графике исходные данные и теоретическую прямую (рис. 1):

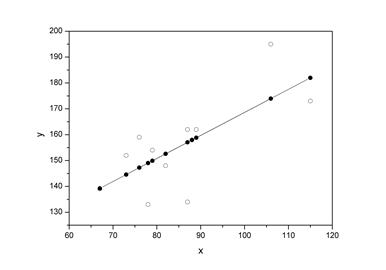
Рис. 1.

Пример 2. По семи предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (y, млн. руб.) от объема капиталовложений (x, млн. руб.).

y
x

Требуется:

1. Для характеристики y от x построить следующие модели:

– линейную (для сравнения с нелинейными),

– степенную,

– показательную,

– гиперболическую.

2. Оценить каждую модель, определив:

– индекс корреляции,

– среднюю относительную ошибку,

– коэффициент детерминации,

– F-критерий Фишера.

3. Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.

4. Рассчитать прогнозные значения результативного признака по лучшей модели, если объем капиталовложений составит 89,573 млн. руб.

5. Результаты расчетов отобразить на графике.

Решение:

Построение линейной модели парной регрессии

Определим линейный коэффициент парной корреляции по следующей формуле:

;

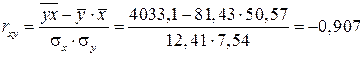Можно сказать, что связь между объемом капиталовложений x и объемом выпуска продукции y обратная, достаточно сильная.

Уравнение линейной регрессии имеет вид: .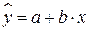

Значения параметров a и b линейной модели определим, используя данные таблицы 1

,

.

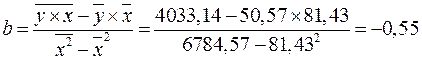Уравнение линейной регрессии имеет вид:

.

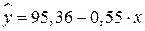С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции уменьшится в среднем на 550 тыс. руб. Это свидетельствует о неэффективности работы предприятий, и необходимо принять меры для выяснения причин и устранения этого недостатка.

Рассчитаем коэффициент детерминации:

.

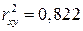Вариация результата y (объема выпуска продукции) на 82,2 % объясняется вариацией фактора x (объемом капиталовложений).

Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

.

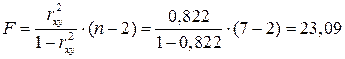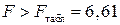для a = 0,05; , .

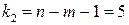Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. .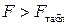

Определим среднюю относительную ошибку:

.

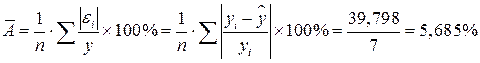В среднем расчетные значения 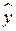для линейной модели отличаются от фактических значений на 5,685%.

 

Таблица 1

	y	x	y×x	x2
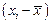
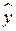
					13,43	180,36	‑17,4	303,8	60,2	3,84	6,000
					5,43	29,485	‑13,4	180,36		‑1,96	‑3,500
					1,43	2,0449	0,57	0,3249	50,3	1,74	3,346
					‑2,57	6,6049	‑5,43	29,485	53,6	‑5,56	‑11,583
					‑0,57	0,3249	2,57	6,6049	49,2	0,84	1,680
					‑4,57	20,885	14,57	212,28	42,6	3,44	7,478
					‑12,6		18,57	344,84	40,4	‑2,36	‑6,211
Итого					0,01	397,71		1077,7		‑0,02	39,798
Ср. знач.	50,57	81,43	4033,14	6784,57							5,685
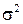
	56,8
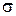
	7,54	12,41