КОНТРОЛЬНАЯ РАБОТА № 6

 

1. Найти наибольшую λ_max и наименьшую λ_min длины волн спектра атома водорода серии Бальмера.

2. При переходе электрона в атоме водорода из возбуждённого состояния в основное радиус боровской орбиты электрона уменьшился в 25 раз. Определить длину волны λ излученного фотона.

3. Вычислить кинетическую энергию электрона, выбитого из второго энергетического уровня атома водорода фотоном, длина волны которого λ = 0,2 мкм.

4. Определить наименьшее и наибольшее значения энергии фотона в инфракрасной серии спектра водорода (серия Пашена).

5. Атом водорода находится в возбуждённом состоянии с главным квантовым числом 3. Падающий фотон выбивает из атома электрон, сообщая ему кинетическую энергию 2,5 эВ. Вычислить энергию падающего фотона.

6. Период полураспада изотопа ₃₃As⁷⁴ равен 17,5 суток. Определить постоянную распада и среднюю продолжительность жизни атомов этого изотопа.

7. Период полураспада радиоактивного аргона ₁₈Аr⁴¹ равен 110 мин. Определить время, в течение которого распадается 25% начального количества атомов.

8. Вещество ₁₁Na²³ облучается дейтронами и превращается в радиоактивный изотоп ₁₁Na²⁴ с периодом полураспада 11,5 ч. Какая доля радиоактивного натрия остается через сутки после прекращения облучения дейтронами?

9. За полгода распалось 40% некоторого исходного радиоактивного элемента. Определить период полураспада этого элемента.

10. Постоянная радиоактивного распада равна 3,28×10^-9 с^-1 для элемента ₈₈Ra²²⁸. Определить, какая часть ядер этого элемента останется через 5 лет.

11. Энергия возбуждённого атома водорода 0,85 эВ. Вычислить длину волны де Бройля электрона на этой орбите.

12. Протон движется со скоростью 1×10⁷ м/с. Определить длину волны де Бройля протона.

13. Дебройлевская длина волны электрона уменьшилась с 1 до 0,5 нм. На сколько изменилась энергия электрона?

14. Найти длину волны де Бройля для протона, прошедшего разность потенциалов 1000 кВ.

15. Вычислить длину волны де Бройля для молекулы азота, движущейся со средней скоростью, соответствующей комнатной температуре.

16. Длина волны де Бройля для электрона равна 1,3 нм. Определить скорость электрона.

17. Скорость электронов равна 0,8×с. Найти длину волны де Бройля электронов.

18. Коротковолновая граница рентгеновского спектра 0,2×10^-10 м. Определить длину волны де Бройля для электронов, бомбардирующих антикатод.

19. Вычислить длину волны де Бройля для электрона обладающего кинетической энергией 1 эВ.

20. Определить длину волны де Бройля для α-частиц, прошедших разность потенциалов: 1) 200 В; 2) 100 кВ.

21. Рентгеновские лучи с длиной волны λ = 0,052 нм выбивают электроны с K-уровня атома молибдена. Какова скорость выбитых электронов?

22. Межплоскостное расстояние в кристалле марганца равно 2,4×10^-10 м. Определить, при какой длине волны рентгеновских лучей первый максимум при отражении будет наблюдаться под углом 15°. Найти минимальное напряжение на рентгеновской трубке.

23. Найти наибольшую длину волны K-серии рентгеновского излучения от золотого антикатода.

24. Расстояние между атомными плоскостями кристалла 3×10^-8 см. Рентгеновские параллельные лучи, падающие на кристалл, дают при отражении первый максимум под углом 30°. Под каким минимальным напряжением работает рентгеновская трубка?

25. Рентгеновская трубка работает при напряжении 41 кВ и излучение трубки падает на кристалл. Угол между плоскостью кристалла и пучком рентгеновских лучей, при котором наблюдается второй максимум отражения, равен 5°44'. Определить расстояние между атомными плоскостями кристалла.

26. При каком наименьшем напряжении на рентгеновской трубке с железным антикатодом появляются линии К_α?

27. Какую наименьшую разность потенциалов нужно приложить к рентгеновской трубке с вольфрамовым антикатодом, чтобы в спектре излучения вольфрама были все линии K-серии?

28. При переходе электрона в атоме меди с M-слоя на L-слойиспускаются лучи с длиной волны 12×10^-10 м. Вычислить постоянную экранирования в формуле Мозли.

29. Наибольшая длина волны К-серии рентгеновского излучения равна 1,94×10^-10 м. Из какого материала сделан антикатод?

30. Найти коротковолновую границу рентгеновского спектра при условии, что к рентгеновской трубке приложена разность потенциалов: 1) 20 кВ; 2) 100 кВ.

31. Используя соотношение неопределённостей Гейзенберга, вычислить ошибку в измерении скорости электрона, зарегистрированного в пузырьковой камере. Диаметр пузырька считать равным d = 1 мкм, а скорость электрона u = 10⁷ м/с.

32. Движение электронов в электронно-лучевой трубке в первом приближении можно рассматривать как движение частиц, происходящее по траектории. След электронного пучка на экране имеет радиус порядка 10^-4 см. Длина трубки 15 см, напряжение на ней 10⁴ В. Оценить неопределённость в определении импульса электрона для этого случая.

33. Найти ошибку в определении скорости электрона, протона и пылинки массой 0,1 нг, если их координаты установлены с неопределённостью 1 мкм.

34. Электрон движется в атоме водорода со скоростью 2,2×10⁸ см/с. Показать, что неопределённость в измерении скорости по порядку величины равна самой скорости.

35. Положение молекулы водорода и положение электрона определены с ошибкой 10^-7 м. Какова будет неопределённость в скорости для молекулы водорода и электрона?

36. Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике. Определить значения энергии электрона на первом, втором и т. д. энергетических уровнях, если ширина ящика 10^-10 м. Построить график зависимости энергии электрона от номера энергетического уровня.

37. Ширина одномерного прямоугольного потенциального ящика равна 500 пм. Определить в электрон-вольтах разность энергий второго и первого, одиннадцатого и десятого энергетических уровней электрона.

38. Электрон находится в потенциальном ящике, ширина которого принимает значения: 0,1 нм; 1 нм; 10 нм; 0,02 м; 0,1 м. Определить разность энергий электрона на первом и втором энергетических уровнях. Оценить полученные результаты с точки зрения проявления квантовых свойств рассматриваемой системы.

39. Электрон находится в потенциальном ящике. Определить вероятность того, что электрон находится на втором энергетическом уровне в интервале 0 < х < l/2.

40. В потенциальном ящике шириной l находится электрон на третьем энергетическом уровне. Определить, в каких точках интервала 0<х<l плотность вероятности нахождения электрона равна нулю. Определить вероятность того, что электрон находится на участке интервала l/3<х<(2/3)l.

41. Вычислить толщину слоя половинного ослабления при условии, что узкий пучок g-излучения с энергией 1,25 МэВ проходит через свинцовый экран.

42. Определить, как изменится интенсивность узкого пучка g-лучей при прохождении через экран, состоящий из двух плит: алюминиевой — толщиной 10 см и железной — толщиной 5 см. Коэффициенты линейного ослабления для А1 m₁ = 0,1 см^-1, а для Fe m₂ = 0,3 см^-1.

43. Как изменится степень ослабления g-лучей при прохождении через свинцовый экран, если длина волны этих лучей 4,1×10^-13 и 8,2×10^-13 м, толщина экрана 1 см.

44. Вычислить толщину слоя половинного ослабления для свинцового экрана, через который проходит монохроматический узкий пучок g-лучей с длиной волны 6×10^-13 м.

45. Какова энергия g-лучей, если при прохождении через слой железа толщиной в 3,15 см интенсивность излучения ослабляется в 4 раза?

46. Радиоактивное ядро, состоящее из 5 протонов и 5 нейтронов, выбросило α-частицу. Какое ядро образовалось в результате α-распада? Определить энергию связи образовавшегося ядра.

47. Вычислить энергию связи ядра и его удельную энергию связи, т. е. энергию, приходящуюся на один нуклон для элемента ₇₉Аu¹⁹⁶.

48. Определить энергию связи ядра и его удельную энергию связи для элемента ₅₅Cs¹³².

49. В какой элемент превращается ₉₂U²³⁸ после трех α-распадов и двух β-превращений? Решение пояснить схемой.

50. Радиоактивное ядро, состоящее из 90 протонов и 138 нейтронов, выбросило α-частицу. Какое ядро образовалось в результате α-распада? Определить энергию связи образовавшегося ядра.

51. Определить пороговую энергию образования электронно-позитронной пары в кулоновском поле электрона, которая происходит по схеме g + е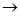^- e^- + e⁺ + е^-.

52. Под действием g-лучей идут реакции типа (g, n), (g, p) и (g, α), которые получили название ядерный фотоэффект. Впервые ядерный фотоэффект наблюдался в 1934 г. Дж. Чедвиком на примере фоторасщепления дейтрона g + ₁H² 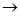п + р. Определить пороговую энергию g-лучей, при которой возможно фоторасщепление дейтрона и энергию связи дейтрона.

53. Считая, что рождение π ⁺-мезонов происходит по схеме р + р 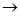р + п + π⁺, определить порог рождения π⁺-мезонов, т.е. минимальную кинетическую энергию бомбардирующего протона, необходимую для образования π ⁺-мезона. Массу π ⁺-мезона принять равной 0,150 а. е. м.

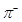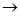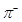54. Рождение -мезонов происходит по схеме п+n п+р+ . Определить порог рождения 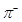-мезона, т.е. минимальную кинетическую энергию бомбардирующего нейтрона, необходимую для образования 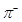-мезона. Массу 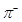-мезона принять равной 0,150 а. е. м.

55. Вычислить энергию, которая выделяется в ядерной реакции синтеза:

₁H² + ₁H³ 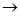₂He⁴ + n .

56. Вычислить энергию ядерной реакции ₂He⁴ + n 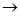₁H³ + p.

57. Вычислить энергию ядерной реакции ₁₃Al²⁷ + п 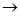₁₂Mg²⁷ + р.

58. Вычислить энергию ядерной реакции ₁₆S³³ + п 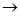₁₅Р³³ + р.

59. Вычислить энергию ядерной реакции ₁Н² + ₃Li⁷ 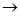2 ₂Не⁴ + п.

60. Вычислить энергию ядерной реакции ₃Li⁷ + p 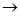(₄Be⁷)* + n , где (₄Be⁷)* 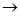₄Ве⁷ +g + 430 кэВ.

61. Определить плотность вольфрама (решётка объёмно-центрированная кубическая), если расстояние между ближайшими соседними атомами равно 0,273 нм.

62. Платина имеет гранецентрированную кубическую кристаллическую решётку. Определить параметр а решётки и расстояние между ближайшими соседними атомами. Плотность платины 21,45×10³ кг/м³.

63. Найти плотность хрома, если известно, что кристаллическая решётка объёмно-центрированная кубическая. Постоянная решётки а = 0,288 нм.

64. Расстояние между ближайшими соседними атомами кристаллической решётки свинца равно 0,349 нм. Определить параметр а решётки и плотность свинца, если решётка гранецентрированная кубическая.

65. Литий имеет объёмно-центрированную кристаллическую решётку. Расстояние между двумя ближайшими атомами равно 0,303 нм. Определить плотность лития.

66. Образец магния массой 50 г нагревается от 0 до 20 К. Определить теплоту, необходимую для нагревания. Принять характеристическую температуру Дебая для магния 400 К и считать условие Т<<Θ_D выполненным.

67. Вычислить по теории Дебая удельную теплоёмкость серебра при температуре 8 К. Считать условие Т<<Θ_D выполненным и принять для серебра Θ_D = 225 К.

68. Молярная теплоёмкость молибдена при температуре 20 К равна 0,6 Дж/(моль×К). Вычислить характеристическую температуру Дебая Θ_D. Условие Т<<Θ_D считать выполненным.

69. Определить теплоту, необходимую для нагревания двух молей никеля от 20 до 30 К. Принять характеристическую температуру Дебая для никеля Θ_D = 450 К и условие Т<<Θ_D считать выполненным.

70. Вычислить по теории Дебая удельную теплоёмкость германия при температуре 20 К. Принять для германия Θ_D = 370 К и условие Т<<Θ_D считать выполненным.

ПРИЛОЖЕНИЯ

1. Основные физические постоянные (округлённые значения)

Физическая постоянная	Обозначение	Значение
Ускорение свободного падения	g	9,81 м/c2
Гравитационная постоянная	G	6,67×10-11 м3/(кг×с2)
Постоянная Авогадро	NA	6,02×1023 моль-1
Молярная газовая постоянная	R	8,31 Дж/(моль×К)
Стандартный объём*	Vm	22,4×10-3 м3/моль
Постоянная Больцмана	k	1,38×10-23 Дж/К
Элементарный заряд	e	1,60×10-19 Кл
Скорость света в вакууме	c	3,00×108 м/с
Постоянная Стефана-Больцмана	s	5,67×10-8 Вт/(м2×К4)
Постоянная закона смещения Вина	b	2,90×10-3 м×К
Постоянная Планка	h h	6,63×10-34 Дж×с 1,05×10-34 Дж×с
Постоянная Ридберга	R	1,10×107 м-1
Радиус Бора	a	0,529×10-10 м
Комптоновская длина волны электрона	L	2,43×10-12 м
Магнетрон Бора	mB	0,927×10-23 А×м2
Энергия ионизации атома водорода	Wi	2,18×10-18 Дж (13,6 эВ)
Атомная единица массы	a.e.m.	1,660×10-27 кг
Электрическая постоянная	e0	8,85×10-12 Ф/м
Магнитная постоянная	m0	4p×10-7 Гн/м

* Молярный объём идеального газа при нормальных условиях.

2. Некоторые астрономические величины

Наименование	Значение
Радиус Земли	6,37×106 м
Масса Земли	5,98×1024 кг
Радиус Солнца	6,95×108 м
Масса Солнца	1,98×1030 кг
Радиус Луны	1,74×106 м
Масса Луны	7,33×1022 кг
Расстояние от центра Земли до центра Солнца	1,49×1011 м
Расстояние от центра Земли до центра Луны	3,84×108 м

3. Плотность твёрдых тел

Твёрдое тело	Плотность, кг/м3	Твёрдое тело	Плотность, кг/м3
Алюминий	2,70×103	Медь	8,93×103
Барий	3,50×103	Никель	8,90×103
Ванадий	6,02×103	Свинец	11,3×103
Висмут	9,80×103	Серебро	10,×103
Железо	7,88×103	Цезий	1,90×103
Литий	0,53×103	Цинк	7,15×103

4. Плотность жидкостей

Жидкость	Плотность, кг/м3	Жидкость	Плотность, кг/м3
Вода (при 40С)	1,00×103	Сероуглерод	1,26×103
Глицерин	1,26×103	Спирт	0,80×103
Ртуть	13,6×103

5. Плотность газов (при нормальных условиях)

Газ	Плотность, кг/м3	Газ	Плотность, кг/м3
Водород	0,09	Гелий	0,18
Воздух	1,29	Кислород	1,43

6. Коэффициент поверхностного натяжения жидкостей

Жидкость	Коэффициент, мН/м	Жидкость	Коэффициент, мН/м
Вода		Ртуть
Мыльная пена		Спирт

 

7. Эффективный диаметр молекулы

 

Газ	Диаметр, м	Газ	Диаметр, м
Азот	3,0×10-10	Гелий	1,9×10-10
Водород	2,3×10-10	Кислород	2,7×10-10

 

8. Диэлектрическая проницаемость

 

Вещество	Проницаемость	Вещество	Проницаемость
Вода		Парафин	2,0
Масло транс-форматорное	2,2	Стекло	7,0

 

9. Удельное сопротивление металлов

 

Металл	Удельное сопротивление, Ом×м	Металл	Удельное сопротивление, Ом×м
Железо	9,8×10-8	Нихром	1,1×10-6
Медь	1,7×10-8	Серебро	1,6×10-8

 

10. Энергия ионизации

 

Вещество	Wi, Дж	Wi, эВ
Водород	2,18×10-18	13,6
Гелий	3,94×10-18	24,6
Литий	1,21×10-17	75,6
Ртуть	1,66×10-18	10,4

 

11. Подвижность ионов в газах, м²/(В×с)

 

Газ	Положительные ионы	Отрицательные ионы
Азот	1,27×10-4	1,81×10-4
Водород	5,4×10-4	7,4×10-4
Воздух	1,4×10-4	1,9×10-4

 

12. Показатель преломления

 

Вещество	Показатель	Вещество	Показатель
Алмаз	2,42	Глицерин	1,47
Вода	1,33	Стекло	1,50

 

13. Работа выхода электрона

 

Металл	А, Дж	А, эВ
Калий	3,5×10-19	2,2
Литий	3,7×10-19	2,3
Платина	10×10-19	6,3
Рубидий	3,4×10-19	2,1
Серебро	7,5×10-19	4,7
Цезий	3,2×10-19	2,0
Цинк	6,4×10-19	4,0

 

14. Относительные атомные массы (округлённые значения)

А_r и порядковые номера Z некоторых элементов

Элемент	Символ	Аr	Z	Элемент	Символ	Ar	Z
Азот	N			Марганец	Mn
Алюминий	Al			Медь	Cu
Аргон	Ar			Молибден	Mo
Барий	Ba			Натрий	Na
Ванадий	V			Неон	Ne
Водород	H			Никель	Ni
Вольфрам	W			Олово	Sn
Гелий	He			Платина	Pt
Железо	Fe			Ртуть	Hg
Золото	Au			Сера	S
Калий	K			Серебро	Ag
Кальций	Ca			Углерод	C
Кислород	O			Уран	U
Магний	Mg			Хлор	Cl

 

15. Массы атомов лёгких изотопов

 

Изотоп	Символ	Масса, а.е.м.	Изотоп	Символ	Масса, а.е.м.
Нейтрон		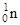1,00867	Азот		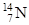14,00307
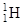
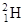
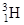
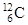
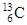
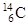
Водород		1,00783 2,01410 3,01603	Углерод		12,00000 13,00335 14,00324
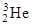
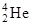
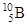
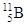
Гелий		3,01603 4,00260	Бор		10,01294 11,00930
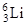
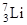
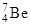
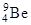
Литий		6,01513 7,01601	Берилий		7,01693 9,01219
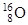
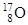
Кислород		15,99491 16,99913

 

16. Периоды полураспада радиоактивных изотопов

 

Изотоп	Символ	Период полураспада
Актиний		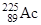10 сут
Иод		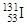8 сут
Кобальт		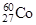5,3 года
Магний		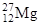10 мин
Радий		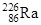1620 лет
Радон		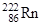3,8 сут
Стронций		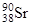27 лет
Фосфор		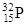14,3 сут
Церий		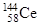285 сут

 

17. Масса и энергия покоя некоторых частиц

Частица	m0	W0
кг	а.е.м.	Дж	МэВ
Электрон	9,11×10-31	0,00055	8,16×10-14	0,511
Протон	1,672×10-27	1,00728	1,50×10-10
Нейтрон	1,675×10-27	1,00867	1,51×10-10
Дейтрон	3,35×10-27	2,01355	3,00×10-10
α-частица	6,64×10-27	4,00149	5,96×10-10
Нейтральный p-мезон	2,41×10-28	0,14498	2,16×10-11

 

18. Единицы SI, имеющие специальные наименования

 

Величина	Единица
Наименование	Размер-ность	Наиме-нование	Обозна-чение	Выражение через основные и дополнитель-ные единицы
Основные единицы
Длина	L	метр	м
Масса	M	килограмм	кг
Время	T	секунда	с
Сила электрического тока	I	ампер	А
Термодинамическая температура	q	кельвин	К
Количество вещества	N	моль	моль
Сила света	J	кандела	кд
Дополнительные единицы
Плоский угол	¾	радиан	рад
Телесный угол	¾	стерадиан	ср
Производные единицы
Частота	Т-1	герц	Гц	с-1
Сила, вес	LMT-2	ньютон	Н	м×кг×с-2
Давление, механическое напряжение	L-1MT-2	паскаль	Па	м-1×кг×с-2
Энергия, работа, количество теплоты	L2MT-2	джоуль	Дж	м2×кг×с-2
Мощность, поток энергии	L2MT-3	ватт	Вт	м2×кг×с-3
Количество электричества (электрический заряд)	TI	кулон	Кл	с×А
Электрическое напряжение, потенциал, разность потенциалов, электродвижущая сила	L2MT-3I-1	вольт	В	м2×кг×с-3×А-1
Электрическая ёмкость	L-2M-1T4I2	фарад	Ф	м-2×кг-1×с4×А2
Электрическое сопротивление	L2MT-3I-2	ом	Ом	м2×кг×с-3×А-2
Электрическая проводимость	L-2M-1T3I2	сименс	См	м-2×кг-1×с3×А2
Магнитный поток	L2MT-2I-1	вебер	Вб	м2×кг×с-2×А-1
Магнитная индукция	MT-2I-1	тесла	Тл	кг×с-2×А-1
Индуктивность, взаимная индуктивность	L2MT-2I-2	генри	Гн	м2×кг×с-2×А-2
Световой поток	J	люмен	лм	Кд×ср
Освещённость	L-2J	люкс	лк	м2×кд×ср
Активность изотопа	T-1	беккерель	Бк	м-×кд
Поглощённая доза излучения	L2I-2	грей	Гр	м2×с-2

 

ПРИМЕЧАНИЯ:

1. Кроме температуры Кельвина (обозначение Т) допускается применять также температуру Цельсия (обозначение t), определяемую выражением t=T−T₀ , где Т₀ =273,15 К. Температура Кельвина выражается в кельвинах, температура Цельсия - в градусах Цельсия (обозначение международное и русское °С. По размеру градус Цельсия равен кельвину.

2. Интервал или разность температур Кельвина выражают в кельвинах. Интервал или разность температур Цельсия допускается выражать как в кельвинах так и в градусах Цельсия.

 

19. Множители и приставки для образования десятичных

кратных и дольных единиц и их наименования

Приставка	Мно- жи- тель	Приставка	Мно- жи- тель
Наиме-нование	Обозна-чение	Наиме-нование	Обозна-чение
экса	Э	1018	деци	д	10-1
пэта	П	1015	санти	с	10-2
тера	Т	1012	милли	м	10-3
гига	Г	109	микро	мк	10-6
мега	М	106	нано	н	10-9
кило	К	103	пико	п	10-12
гекто	Г	102	фемто	ф	10-15
дека	да	101	атто	а	10-18

 

20. Греческий алфавит

 

Обозначения букв	Название букв	Обозначения букв	Названия букв
A, a	альфа	N, n	ню
B, b	бета	X, x	кси
G, g	гамма	O, o	омикрон
D, d	дэльта	P, p	пи
E, e	эпсилон	R, r	ро
Z, z	дзета	S, s	сигма
H, h	эта	T, t	тау
q, J	тэта	U, u	ипсилон
I, i	иота	F, j	фи
K, k	каппа	C, c	хи
L, l	ламбда	Y, y	пси
M, m	ми	W, w	омега

 

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

 

1. Трофимова Т.И. Курс физики. Учеб. пособие для вузов. — М.: Высш. шк. 2003. — 478 с.

2. Детлаф А.А., Яворский Б.М. Курс физики: Учеб. пособие для втузов. — М.: Высш. шк. 1989. — 608 с.

3. Волькенштейн В.С. Сборник задач по общему курсу физики. — М.: Высш. шк. 1990. — 464 с.

4. Чертов А.Г., Воробьёв А.А. Задачник по физике: Учеб. пособие для втузов. — М.: Высш. шк. 1988. — 527 с.

5. Трофимова Т.И., Павлова З.Г. Сборник задач по курсу физики с решениями. Учеб. пособие для вузов. — М.: Высш. шк. 2001. — 591 с.

 

 

СОДЕРЖАНИЕ

 

	Стр.
Предисловие
Общие методические указания
Самостоятельная работа по учебным пособиям
Контрольные вопросы на экзаменах по физике для специальностей 15.03.02 (ДО и ЛИД), 35.03.02 (ДМ и ЛМ).
Методические указания к контрольным работам
О приближённых вычислениях
Методические указания к лабораторным работам
Контрольная работа № 1
Контрольная работа № 2
Контрольная работа № 3
Контрольная работа № 4
Контрольная работа № 5
Контрольная работа № 6
Приложения
Рекомендуемая литература
Содержание