Схемы заданной функции

Пример. Рассмотрим базовые элементы: 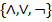. Задача состоит в построении схемы из данных элементов, которая вычисляет функцию суммы двух элементов по модулю ( ).

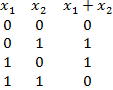
Рассмотрим представление функции в виде СДНФ. Рассмотрим следующий функциональный граф, вершинам которого поставлены в соответствие логические элементы.

ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">

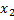
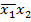
Этот граф естественным образом вычисляет требуемую сумму . Каждая вершина совершает соответствующую ей логическую операцию. Таким образом, подавая на входы данной схемы определенные r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 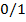значения , на выходе получим требуемую сумму по r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> .

Определение. Схемой из функциональных элементов 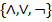называется последовательность элементов, где каждый элемент совершает определенную логическую операцию над результатами, ранее вычисленными операционными элементами.

Удобно графовое представление схемы из функциональных элементов. Рассмотрим ациклический ориентированный граф (ацикличность – отсутствие циклов).

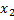
В таком графе обязательно найдется хотябы одна вершина, в которой нет входящих ребер. Такую вершину назовем источником. Аналогично, в таком графе найдется хотябы одна вершина, в которой нет исходящих ребер. Такую вершину назовем стоком.

Причем, рассматривая ациклический граф, число входящих ребер в каждой вершине . Глубиной вершины в таком графе назовем длину максимального пути из источника к данной вершине. Если ребро в графе

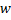
, то глубина вершины меньше глубины вершины ( ).

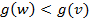Каждой вершине поставим в соответствие функциональный элемент 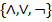. Если у вершины входящих ребра, то это r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 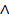или r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> , как элементы с входами. Если у вершины входящее ребро, то поставим в соответствие . Источникам поставим в соответствие переменные 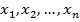. В результате получим схему из функциональных элементов. Каждой вершине схемы соответствует определенная логическая функция от входных переменных 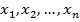, которая определяется индукцией по глубине вершин в схеме. Для источников 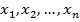это соответствующие тождественные функции. Пусть мы определили функции всех вершин, глубина которых , тогда рассмотрим вершины, глубина которых ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> . Если вершине соответствует элемент r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 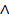, а соответствуют входам элемента, то выходу этого элемента соответствует .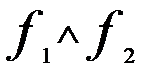

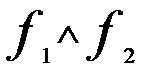
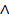
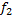
Если вершине соответствует элемент r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> , то получаем соответственно выход . если вершине соответствует элемент , то на выходе получаем отрицание входа.

Таким образом, каждая схема из функциональных элементов вычисляет набор функций от входных элементов 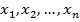, которые определены в стоках программы.

Определение. Сложностью схемы функциональных элементов называется число элементов в ней 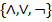. Схема из любых других элементов строится подобным образом. Сложность схемы обозначим .

Определение. Сложностью логической функции 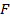будем называть следующую величину 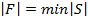, где минимум берется по всем схемам, которые реализуют функцию 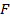, то есть минимальное число элементов “r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 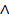” “r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> ” “ ”, необходимое для реализации функции 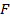с помощью какой-либо схемы.

Определение. Сложностью класса функций K назовем величину

В дальнейшем нас будет интересовать сложность класса всех двоичных функций неболее чем от n :

 

 

Оценим сложность класса двоичных функций не более чем от переменных при больших n. Будем использовать следующие обозначения:

1) 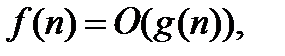, если ;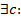

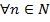2) если ;

3) 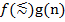, если (“≲” – ассимптотически не превосходит).

Оценим сложность сумматора двух двоичных чисел.

Входами сумматора являются разрядов входных двоичных чисел, а выходами ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> цифр , которые являются разрядами суммы. На рисунке показано подсхем блока, каждый блок соответствует вычислению определенного разряда суммы.

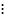
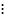
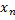
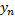
Входом i-ого блока являются входы -ых разрядов суммируемых чисел ( – вход -ого разряда 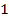-ого числа, – вход -ого разряда -ого числа), а также значение переносимого числа из предыдущего разряда. Выходом i-ого блока является значение двоичной суммы разрядов на входе , а также значение переносимого числа в очередной r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> разряд.

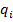
Покажем, что общая сложность сумматора не более, чем линейная. Действительно, сумматор состоит из блоков, поэтому сложность сумматора не превышает (сложность реализации отдельного блока).

Отдельный блок зависит не более чем от -х входов и имеет выхода, тогда сложность реализации отдельного блока не более, чем const. Например, используя представление двоичной функции в виде СДНФ, выход определяется формулой:

Потребуется r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> операции конъюнкции (“r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 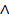”), т.к. в СДНФ слагаемых, в каждом слагаемом операция “r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 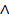” выполняется раза. Операций дизъюнкций (“r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> ”) потребуется и операций отрицания (“ ”). Общее число элементов для реализации -ого выхода: , .

Оценим сложность реализации 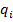. Для этого будем использовать представление в виде СДНФ. 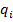имеет единицы, поэтому в СДНФ будет слагаемых, тогда число используемых элементов “r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 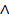” равно , “r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> ” – , “ ” – . Общее число элементов

, следовательно, суммарная сложность сумматора, построенного по СДНФ ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> .

Оценим сложность двоичной функции не более чем от переменных.

При построении схемы, реализуем двоичную функцию не более чем от переменнх. Будем использовать следующие схемы:

6.1 Сложность мультиплексора порядка .

 

1) Мультиплексор порядка

Входами являются переменных , а выходами - переменные 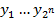. На выходах реализуются всевозможные элементарные конъюнкции (“r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 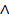”) 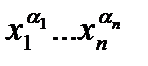. – произвольный набор.

Допустим, что на входе набор и этот набор соответствует двоичному представлению числа . Тогда i- выход мультиплексора будет равен 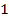, а все остальные выходы , то есть -ый выход мультиплексора реализует следующую логическое умножение: , где – двоичное представление числа :

Таким образом, на выходах мультиплексора реализованы всевозможные элементарные конъюнкции от переменных. Для реализации одной конъюнкции требуется коньюнкция от -х переменных и не более чем отрицаний. Поэтому требуется не более чем элементов. Всего конъюнкций от переменных , следовательно, можно дать следующую оценку сложности мультиплексора:

Оценим сложность мультиплексора более точно, используя полученную оценку. Для этого рассмотрим мультиплексоры порядка от переменных и мультиплексор от оставшихся переменных . Примем , то есть разобьем все переменные на группы. К первой группе относим переменные первой половины , а ко второй группе – переменные второй половины. На выходах реализуются всевозможные элементарные конъюнкции от переменных , а на выходах мультиплексора r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> реализуются всевозможные элементарные конъюнкции переменных . Каждую конъюнкцию от переменных можно получить логическим умножением двух конъюнкций: конъюнкции переменных и конъюнкции переменных . Поэтому общую схему мультиплексора можем представить следующим образом:

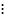
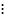
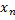
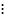
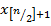
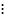
Как показано ранее,

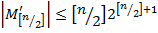
Поэтому общая сложность мультиплексора порядка

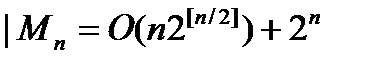
6.2 Сложность дешифратора порядка n.

2) Дешифратор порядка .

У дешифратора имеется входов ( и 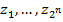) и единственный выход 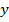. Допустим, что на входах первых переменных двоичный набор , который является двоичным представлением числа , то есть . Тогда на выходе дешифратора будет значение входа : .

Дешифратор реализует следующую двоичную функцию:

(*)

 

 

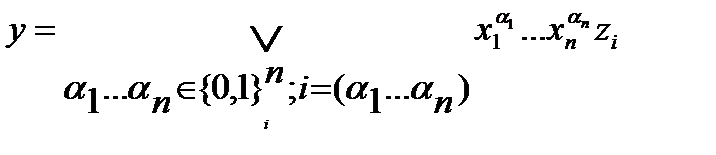Для реализации дешифратора по данной формуле потребуется мультиплексор порядка для реализации всевозможных конъюнкций от переменных , следовательно, сложность дешифратора

, где

· – сложность мультиплексора;

· – умножение выходов мультиплексора на соответствующие входы дешифратора. Элементарные конъюнкции от переменных, т.е. таких умножений ;

· – всевозможные дизъюнкции слагаемых в формуле (*). Количество слагаемых равно числу двоичных наборов от переменных.