Вероятность случайного события

Известно, что в рамках одного опыта одни события появляются чаще, другие - реже. Ясно, что этот факт является объективным свойством каждого события, присущим ему изначально, и не зависит от исследователя. Поэтому можно ввести следующие определение: мера объективной возможности появления события 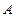в данном опыте называется вероятностью этого события. Она обозначается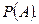

Это определение достаточно естественное, но оно скорее философское, описательное, чем математическое. Ведь если, например, вспомнить пример Бюффона, когда он 4040 раз подбрасывал одну и ту же монету и получил долю выпадений герба 0,508, то, во-первых, ясно, что никто не может поручиться относительно абсолютной симметричности его монеты и абсолютной независимости опыта от помех. Во-вторых, никто не будет возражать, что если бы рядом с Бюффоном кто-то другой свою монету (вроде бы абсолютно симметричную) подбросил те же 4040 раз, то получил бы похожий, но другой результат, например 0,499.

С другой стороны, здравый смысл подсказывает, что если бы оба исследователя увеличивали число подбрасываний, то доли выпадений ребра у обоих исследователей менялись бы, хотя и незначительно. Тот же здравый смысл заставляет нас задуматься: а к какому числу стремились бы эти доли?

Кому надо поверить: Бюффону или другому исследователю? Что принять за вероятность выпадения герба-0,508 или 0,499? И тот и другой результаты являются субъективными, поэтому мы приходим к вынужденной идеализации опыта: мы считаем, что если монета симметрична (идеализация! - такой монеты не существует), то ни у одной ее стороны нет преимуществ при подбрасываниях, поэтому доли выпадения герба надо придать значение 0,5 (50%). Тем самым объективному понятию вероятности случайного события мы придаем числовое измерение!

Исторически математическое понятие вероятности случайного события изменялось, развивалось, совершенствовалось. В настоящее время общепринятым является аксиоматическое построение теории вероятностей, предложенное, как уже упоминалось, А.Н. Колмогоровым.

Вероятность определяется как функция Р(А), ставящая каждому случайному событию А из алгебры событий число. Таким образом, областью определения вероятности является алгебра событий.

Вероятность удовлетворяет системе аксиом (в упрощённом виде):

аксиома 1. 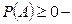вероятность есть число неотрицательное;

аксиома 2. 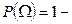вероятность достоверного события равна единице;

аксиома 3. аксиома аддитивности (сложения): если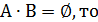

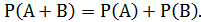
Из аксиом получаем важнейшие следствия.

Следствие 1. 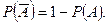- при решении задач бывает легче выяснить 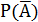, тогда .

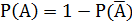Следствие 2.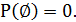

Следствие 3. (теорема сложения). .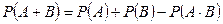

Следствие 4.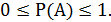

Итак, пространство элементарных событий с помощью операций порождает алгебру событий, которая является областью определения функции – вероятности случайных событий. Эта тройка называется вероятностным пространством.

Рассмотрим два наиболее употребительных вероятностных пространства: геометрическое вероятностное пространство, основанное на геометрическом определении вероятности и классическое вероятностное пространство, основанное на классическом определении вероятности.