 |
Главная |
Нормальное распределение
|
из
5.00
|
Так называется распределение НСВ  , плотность вероятностей которой и функция распределения задаётся формулами:
, плотность вероятностей которой и функция распределения задаётся формулами:
 (27)
(27)
Формулы (27) показывают, что законы распределения зависят от двух параметров 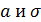 . В силу исключительной роли нормального распределения в теории вероятностей, для обоих законов ввели специальные обозначения:
. В силу исключительной роли нормального распределения в теории вероятностей, для обоих законов ввели специальные обозначения:

 .
.
Отметим основные свойства нормального распределения.
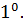 Выполняется основное условие плотности вероятности:
Выполняется основное условие плотности вероятности: 
 Построим график функции
Построим график функции  Во-первых, отметим симметричность графика относительно прямой
Во-первых, отметим симметричность графика относительно прямой 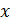 =
=  , причём в точке
, причём в точке 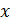 =
=  имеем максимум
имеем максимум 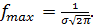 График расположен выше оси ох. Приравнивая вторую производную нулю, получим точки перегиба:
График расположен выше оси ох. Приравнивая вторую производную нулю, получим точки перегиба: 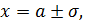
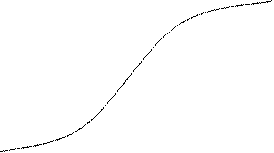
Графики  изображены на рис. 21 и 22.
изображены на рис. 21 и 22.


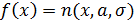 F(x)
F(x) 


| |










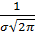












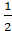
 |  | ||||||
 |  | ||||||





 |  |
0 a-  a a+
a a+  x 0
x 0 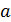 x
x
|
|
Следует обратить внимание на рис.21 – график плотности вероятности нормального распределения, знаменитую колоколообразную кривую, которая называется кривой Гаусса. Какие бы значения 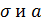 ни задавать, площадь под соответствующей кривой будет равна единице. Посмотрите кругом и увидите контуры, похожие на кривую Гаусса – очертание крон деревьев; контур кучи песка; очертание гор и холмов на горизонте, наконец, сам колокол, издающий волшебные звуки. В разделе «предельные теоремы теории вероятностей» мы ещё будем иметь повод упомянуть исключительную роль нормального закона.
ни задавать, площадь под соответствующей кривой будет равна единице. Посмотрите кругом и увидите контуры, похожие на кривую Гаусса – очертание крон деревьев; контур кучи песка; очертание гор и холмов на горизонте, наконец, сам колокол, издающий волшебные звуки. В разделе «предельные теоремы теории вероятностей» мы ещё будем иметь повод упомянуть исключительную роль нормального закона.
 Числовые характеристики нормального распределения:
Числовые характеристики нормального распределения:
 . Таким образом, получен вероятностный смысл параметров
. Таким образом, получен вероятностный смысл параметров 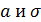 нормального распределения:
нормального распределения: 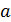 – это математическое ожидание, а
– это математическое ожидание, а 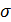 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Как известно, с помощью законов распределения вычисляются вероятности 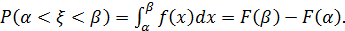
В случае нормального распределения F(x) выражается в виде интеграла (см. формулу (27)), причём этот интеграл «не берётся», т.е. не выражается в элементарных функциях. Таким образом, указанную вероятность можно вычислять, причём лишь приближённо, только по формуле:
 (28)
(28)
Однако этот интеграл зависит ещё и от двух параметров:  ! Не составлять же множество таблиц для разных
! Не составлять же множество таблиц для разных 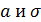 !? Выручает замечательное свойство нормального распределения:
!? Выручает замечательное свойство нормального распределения:
 (29)
(29)
Формула (29) показывает, во-первых, что таблицы следует составить лишь для стандартного нормального распределения, т.е. при 
Во-вторых, получим удобную формулу для вычисления упомянутых вероятностей:

 (30)
(30)
где  и для этой функции составлены таблицы.
и для этой функции составлены таблицы.
Формула (30) – лишь одна из формул, использующая стандартное нормальное распределение. Рассмотрим ещё одну:
 (31)
(31)
где 
 - стандартная функция Лапласа.
- стандартная функция Лапласа.
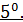 Правило трёх сигм.
Правило трёх сигм.
Мы ранее подчёркивали, что среднее квадратическое отклонение характеризует отклонение значений СВ от своего математического ожидания. Найдём для нормального распределения вероятности попадания СВ в окрестности математического ожидания радиусов, кратных 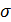 :
:

1)Пусть k=1 
2)Пусть k=2 
3)Пустьk=3 
Таким образом, попадание нормально распределённой СВ в окрестность матожидания радиуса 3  есть практически достоверное событие
есть практически достоверное событие  . Поэтому на практике обычно ограничиваются изучением СВ в этой окрестности, экономя тем самым определённые ресурсы.
. Поэтому на практике обычно ограничиваются изучением СВ в этой окрестности, экономя тем самым определённые ресурсы.
Пример 42. Время безотказной работы (или пробег) автомобиля в теории эксплуатации автомобиля (ТЭА) называется наработкой. Наработка до первого отказа подчиняется нормальному закону.
Пусть математичекое ожидание равно 95 тыс. км.,С.К.О. 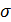 =30 тыс. км. Требуется:
=30 тыс. км. Требуется:
1) определить вероятность первого отказа с начала эксплуатации до наработки 70 тыс. км;
2) определить вероятность отказа в интервале пробега от 70 тыс. км до 125 тыс. км.
Решение. а) Обозначим  = (наработка автомобиля до первого отказа). По условию
= (наработка автомобиля до первого отказа). По условию 
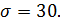 Тогда
Тогда

Таким образом, приблизительно 20% автомобилей потребуют замены деталей при пробеге до 70 тыс. км.
б) 

Это означает, что около 64% автомобилей потребуют ремонта или замены запасными частями на пробеге от 75 до 125 тыс. км.
|
из
5.00
|
Обсуждение в статье: Нормальное распределение |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

