 |
Главная |
Случайные величины (СВ)
|
из
5.00
|
В предыдущих параграфах были рассмотрены случайные события. Однако следует сказать, что основным понятием теории вероятности является понятие случайной величины (СВ). Дадим следующие нестрогое определение. Случайной величиной будем называть переменную величину, которая в результате опыта может принимать значения (заранее не известно какие) из некоторого диапазона.
Пример 29. Число зёрен в колосе пшеницы.
Пример 30. Продолжительность безотказной работы приборов, изготавливаемых на некотором предприятии.
Пример 31. Выработка рабочих некоторого цеха в процентах к предыдущему отчётному сроку.
Пример 32. Вес осколка снаряда.
Пример 33. Количество бракованных изделий в партии деталей.
Пример 34. Число пассажиров в автобусе.
Число таких примеров можно множить сколько угодно. Из приведённых примеров видно, что СВ бывают дискретными (ДСВ) и непрерывными (НСВ). Значения, которые принимает ДСВ, отстоят друг от друга на некотором расстоянии, т.е. в интервале между двумя соседними значениями ДСВ нет других значений этой ДСВ (примеры 29, 33, 34). Значения НСВ сплошь заполняют некоторый интервал, т.е. в этом интервале (диапазоне) мы не можем «запретить» случайной величине принять любое значение (примеры 30-32).
Полную информацию случайным величинам доставляют их законы распределения, под которыми понимают соотношения между значениями, которые могут принимать СВ и соответствующими вероятностями. Как увидим в дальнейшем, принципиальной разницы между ДСВ и НСВ не существует, хотя математическое их описание часто различается. Поэтому начнём изучение СВ раздельно. Случайные величины будем обозначать греческими буквами  а их значения буквами
а их значения буквами  ..
..
Ряд распределения ДСВ
ДСВ может принимать конечное число значений (см. примеры предыдущего параграфа), а также и бесконечное, но счётное, число значений, т.е. их можно пересчитать (пронумеровать). В дальнейшем чаще (для кратности записи) будем рассматривать ДСВ с конечным числом значений.
Итак, пусть ДСВ 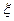 принимает n значений; расположим их в порядке возрастания
принимает n значений; расположим их в порядке возрастания  и составим следующую таблицу:
и составим следующую таблицу:

| 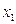
| 
| … | 
| |
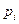
| 
|  
| … | 
| 
|
В этой таблице в верхней строке перечислены в порядке возрастания все значения ДСВ, а во второй строке – соответствующие вероятности случайных событий  , т.е.
, т.е.  . Таким образом, ДСВ состоит из нескольких случайных событий
. Таким образом, ДСВ состоит из нескольких случайных событий  .
.
Поскольку в верхней строке перечислены все значения ДСВ, а в результате опыта принимается какое-нибудь одно значение, то события  попарно несовместные. Следовательно, обязательно выполняется условие
попарно несовместные. Следовательно, обязательно выполняется условие  .Так построенная таблица называется рядом распределения ДСВ. Ряд распределения ДСВ изображается графически в виде многоугольника распределения – фигуры, состоящей из точек
.Так построенная таблица называется рядом распределения ДСВ. Ряд распределения ДСВ изображается графически в виде многоугольника распределения – фигуры, состоящей из точек  и для наглядности соединённых отрезками (рис. 10).
и для наглядности соединённых отрезками (рис. 10).

 P P
P P













 3/8
3/8




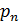
















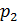



















 1/8
1/8


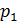


















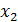

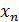 x 0 1 2 3 x
x 0 1 2 3 x
Рис. 1 0 Рис.11
Пример 35. Монета подбрасывается три раза. Построить ряд и многоугольник распределения числа появлений герба.
Решение. Введём ДСВ  (число появлений герба при трёх подбрасываниях монеты). Ясно, что
(число появлений герба при трёх подбрасываниях монеты). Ясно, что 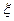 может принимать значения 0,1,2,3 и соответствующие вероятности вычисляются по формуле Бернулли:
может принимать значения 0,1,2,3 и соответствующие вероятности вычисляются по формуле Бернулли:

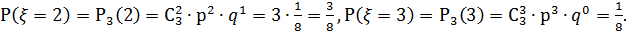
Таким образом, ряд распределения имеет вид:

| |||||
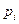
| 1/8 | 3/8 | 3/8 | 1/8 | 
|
Многоугольник распределения изображён на рис.11.
Поскольку ряд распределения является законом распределения, т.е. несёт полную информацию о ДСВ, то с его помощью можно вычислить любую вероятность. Например, вероятность того, что число гербов при трёх подбрасываниях монеты будет не менее одного, равна 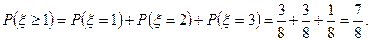
|
из
5.00
|
Обсуждение в статье: Случайные величины (СВ) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

