 |
Главная |
Формула полной вероятности и формулы Байеса
|
из
5.00
|
Своеобразным обобщением формул сложения и умножения вероятностей является формула полной вероятности. Суть в том, что часто бывает так, что опыт состоит из двух этапов.
Пример 21. Имеются две урны. В первой находятся 2 белых и 5 красных шаров; во второй – 7 белых и 3 красных. Наугад выбирается урна и извлекается шар. Какова вероятность того, что извлеченный шар-красный?
В этой задаче сначала требуется выбрать урну (первый этап), а уж затем извлечь шар (второй этап). Для решения подобных задач и применяется формула полной вероятности.
Определение. Пусть событие А появляется вместе с событиями  которые называются гипотезами, если они обладают двумя свойствами:
которые называются гипотезами, если они обладают двумя свойствами:
1)  - в результате опыта какая-нибудь гипотеза осуществится обязательно,
- в результате опыта какая-нибудь гипотеза осуществится обязательно,
2)  - никакие две гипотезы вместе не происходят.
- никакие две гипотезы вместе не происходят.
Следовательно, в результате опыта осуществляется одна и только одна какая - нибудь гипотеза, т.е. Р( 
В примере 21 гипотезы: 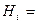 (выбирается
(выбирается  я урна),
я урна), 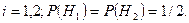
Теорема (формула полной вероятности). Пусть событие 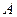 может произойти с каждой из гипотез
может произойти с каждой из гипотез  с условными вероятностями
с условными вероятностями  Тогда вероятность события
Тогда вероятность события 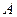 в данном опыте (полная вероятность) вычисляется по формуле полной вероятности:
в данном опыте (полная вероятность) вычисляется по формуле полной вероятности:
 (11)
(11)
Пример 21. Его условие не переписываем. Вводим гипотезы
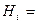 (выбирается
(выбирается  урна),
урна), 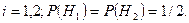 Обозначим событие
Обозначим событие
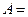 (извлекается красный шар). Из условия задачи ясно, что P(A/
(извлекается красный шар). Из условия задачи ясно, что P(A/  =5/7,
=5/7,
P(A/  )=3/10. Тогда по формуле полной вероятности
)=3/10. Тогда по формуле полной вероятности
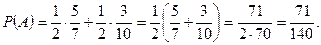
Заметим, что полная вероятность Р(А) – это усреднённый показатель – она всегда находится между наименьшей и наибольшей условными вероятностями Р(А/ 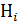 ).
).
В примере 21: 
Важно отметить, что в данном примере хотя урны и неотличимы (вероятности выбора урн одинаковы), их вклад в полную вероятность различен – в 1-й урне доля красных шаров больше  По этой причине, если стало известно, что событие
По этой причине, если стало известно, что событие 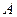 произошло (извлечен красный шар), то у нас будет больше оснований считать, что шар вынут из 1-й урны (реализовалась гипотеза
произошло (извлечен красный шар), то у нас будет больше оснований считать, что шар вынут из 1-й урны (реализовалась гипотеза  ). Другими словами, после получения дополнительной информации (событие
). Другими словами, после получения дополнительной информации (событие 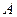 произошло), априорные вероятности гипотез должны быть пересчитаны. Эти послеопытные вероятности гипотез (апостериорные вероятности) пересчитываются по формулам Байеса:
произошло), априорные вероятности гипотез должны быть пересчитаны. Эти послеопытные вероятности гипотез (апостериорные вероятности) пересчитываются по формулам Байеса:

=  ,
,  (12)
(12)
Пример 22. Студенты группы по-разному подготовились к экзамену: 6 человек подготовились отлично (знают все 20 вопросов программы); 8 человек подготовились хорошо (знают 16 вопросов программы); 4 человека подготовились средне (знают 10 вопросов программы); 2 студента подготовились плохо (знают 5 вопросов программы). На экзамене студент получает 2 вопроса. Определить вероятность того, что студент, ответивший на оба вопроса, является
а) отличником; б) хорошистом; в) середняком; г) плохо успевающим студентом?
Решение. Обозначим событие 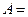 {студент ответил на оба вопроса}, вводим гипотезы:
{студент ответил на оба вопроса}, вводим гипотезы:  {студент – отличник},
{студент – отличник},  {студент- хорошист};
{студент- хорошист};  ={студент – середняк};
={студент – середняк};  {студент является плохо успевающим}. Т.к. в группе всего 20 студентов, то по условию задачи
{студент является плохо успевающим}. Т.к. в группе всего 20 студентов, то по условию задачи  Проверяем:
Проверяем: 
Для формул Байеса сначала надо вычислить полную вероятность.

Вычислим условные вероятности:
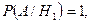 т.к. отличники знают все вопросы.
т.к. отличники знают все вопросы.
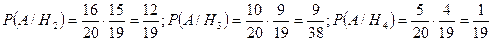 .
.
Следовательно,

Как видим, из четырёх слагаемых, дающих сумму 0,605, вклад наибольший у первого и второго. Вычислим по формулам Байеса апостериорные (условные) вероятности гипотез:



 Проверяем:
Проверяем:  .
.
Видим, что вероятности гипотез сильно перераспределились: до опыта на первые две гипотезы приходилось 0,3+0,4 =0,7, а после опыта 0,446 +0,418 = =0,914. Вместе с тем при заданном уровне подготовки к экзамену, если студент ответил на оба вопроса билета, то вероятность того, что этот студент – отличник (и ему надо ставить отличную оценку?) равна лишь 0,496 (меньше 50%) и для хорошиста – 0,418. Правда, для двоечника такая вероятность совсем малая – 0,008. В любом случае у преподавателя лучший выход для объективной оценки – задавать дополнительные вопросы.
Пример 23. В ящике лежат 25 теннисных мячей – 20 новых и 5 играных. Для игры наудачу выбирают 4 мяча и после игры возвращают в ящик. Затем для второй игры также наудачу берут 2 мяча. Какова вероятность, что вторая игра будет проводиться старыми мячами?
Решение. Вводим гипотезы 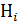 = {для первой игры взято i старых мяча}, i = 0,1,2,3,4. Найдём вероятности гипотез по формулам комбинаторики.
= {для первой игры взято i старых мяча}, i = 0,1,2,3,4. Найдём вероятности гипотез по формулам комбинаторики. 
 Проверяем:
Проверяем: 
Далее обозначаем событие А = {вторая игра будет проводиться старыми мячами} и вычисляем условные вероятности 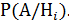
Если осуществилась гипотеза  то для первой игры взято ноль старых мячей, т.е. 4 новых и для второй игры эти мячи уже будут играными – из 25 мячей новых станет 16 и 9 играных, поэтому
то для первой игры взято ноль старых мячей, т.е. 4 новых и для второй игры эти мячи уже будут играными – из 25 мячей новых станет 16 и 9 играных, поэтому 
Аналогично, 

По формуле полной вероятности получаем 
= 
+ 
|
из
5.00
|
Обсуждение в статье: Формула полной вероятности и формулы Байеса |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

