 |
Главная |
Гипотетическая интерпретация выборочных данных (ГИВД). Точечное оценивание параметров распределений. Требования к точечным оценкам
|
из
5.00
|
Содержание этого параграфа можно сформулировать как совокупность методов, позволяющих делать выводы о числовых параметрах распределения генеральной совокупности по случайной выборке из нее. Изучаемый признак Х, проявляющийся во всей генеральной совокупности, является случайной величиной. Закон распределения признака Х содержит некоторые числовые параметры (например, математическое ожидание и дисперсию). Если, например, нас интересует математическое ожидание генеральной совокупности, то задача заключается в том, чтобы по выборочным данным найти такую характеристику, которая давала бы наиболее точное и надежное приближение для неизвестного математического ожидания генеральной совокупности.
Пусть Х - признак, т.е. случайная величина, распределенная по некоторому закону с плотностью вероятности  ) , где
) , где  - параметр распределения, числовое значение которого неизвестно. О величине параметра
- параметр распределения, числовое значение которого неизвестно. О величине параметра  можно судить только по выборке. Всякую однозначно определенную функцию
можно судить только по выборке. Всякую однозначно определенную функцию  результатов наблюдений
результатов наблюдений  признака Х, с помощью которой судят о значении параметра
признака Х, с помощью которой судят о значении параметра  называют точечной оценкой (или статистикой) параметра
называют точечной оценкой (или статистикой) параметра  и обозначают
и обозначают  :
:  В частности, в качестве оценки математического ожидания
В частности, в качестве оценки математического ожидания  признака можно взять среднюю арифметическую выборочных данных:
признака можно взять среднюю арифметическую выборочных данных:  , где n - объем выборки, а в качестве оценки неизвестной генеральной дисперсии
, где n - объем выборки, а в качестве оценки неизвестной генеральной дисперсии 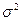 признака можно взять выборочную дисперсию:
признака можно взять выборочную дисперсию: 
В математической статистике результаты  выборочных наблюдений понимают двояко. В первом варианте, при так называемой практической интерпретации выборки, под
выборочных наблюдений понимают двояко. В первом варианте, при так называемой практической интерпретации выборки, под  понимаются фактически наблюденные в конкретном эксперименте значения исследуемого признака Х, т.е. конкретные числа. Во втором варианте, при так называемой гипотетической интерпретации выборочных данных (ГИВД), под
понимаются фактически наблюденные в конкретном эксперименте значения исследуемого признака Х, т.е. конкретные числа. Во втором варианте, при так называемой гипотетической интерпретации выборочных данных (ГИВД), под  понимают лишь обозначения n значений, которые мы могли бы получить, проводя n независимых наблюдений. Действительно, переходя к другой выборке объема n из той же генеральной совокупности получим, вообще говоря, другие результаты наблюдения
понимают лишь обозначения n значений, которые мы могли бы получить, проводя n независимых наблюдений. Действительно, переходя к другой выборке объема n из той же генеральной совокупности получим, вообще говоря, другие результаты наблюдения  . Таким образом, каждое значение
. Таким образом, каждое значение  можно понимать как некоторое значение случайной величины
можно понимать как некоторое значение случайной величины 
 , а выборочная последовательность
, а выборочная последовательность  должна пониматься как реализация n- мерной случайной величины (Х1,Х2,....,Хn), все компоненты Хi которой являются случайными величинами, имеющими одинаковый закон распределения, совпадающий с распределением признака Х. В связи с этим все статистические оценки являются случайными величинами. Действительно, при переходе от одной выборки к другой конкретные значения статистической оценки, подсчитанные по одной и той же формуле, будут подвержены неконтролируемому разбросу. Этот подход (ГИВД) позволяет использовать в математической статистике весь аппарат теории вероятностей, т.е. получает необходимую теоретическую базу.
должна пониматься как реализация n- мерной случайной величины (Х1,Х2,....,Хn), все компоненты Хi которой являются случайными величинами, имеющими одинаковый закон распределения, совпадающий с распределением признака Х. В связи с этим все статистические оценки являются случайными величинами. Действительно, при переходе от одной выборки к другой конкретные значения статистической оценки, подсчитанные по одной и той же формуле, будут подвержены неконтролируемому разбросу. Этот подход (ГИВД) позволяет использовать в математической статистике весь аппарат теории вероятностей, т.е. получает необходимую теоретическую базу.
Пример 5. Пусть выборка  извлечена из нормальной генеральной совокупности признака Х с плотностью вероятности
извлечена из нормальной генеральной совокупности признака Х с плотностью вероятности 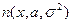 , т.е. М(Х)=
, т.е. М(Х)=  ,
,  . В качестве оценки
. В качестве оценки  неизвестного математического ожидания
неизвестного математического ожидания  возьмем выборочное среднее арифметическое
возьмем выборочное среднее арифметическое
 ,
,
где в соответствии с ГИВД случайные величины Хi , 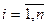 , распределены по тому же закону, что и признак Х, т.е. с плотностью вероятности нормального распределения
, распределены по тому же закону, что и признак Х, т.е. с плотностью вероятности нормального распределения 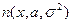 . Средствами теории вероятностей можно доказать, что статистика
. Средствами теории вероятностей можно доказать, что статистика  также распределена по нормальному закону с плотностью вероятности
также распределена по нормальному закону с плотностью вероятности  .
.
Разумеется, значения статистической оценки  , подсчитанные для разных выборок, хотя и подвержены случайному разбросу, должны концентрироваться около истинного значения параметра
, подсчитанные для разных выборок, хотя и подвержены случайному разбросу, должны концентрироваться около истинного значения параметра  . Однако по причине случайности выборки мы не застрахованы полностью даже от большой ошибки. Значит, гарантировать эту желательную близость оценки
. Однако по причине случайности выборки мы не застрахованы полностью даже от большой ошибки. Значит, гарантировать эту желательную близость оценки  к оцениваемому параметру
к оцениваемому параметру  можно только с некоторой вероятностью, причем стремление увеличить эту вероятность приводит к увеличению объема выборки. Необходимо отметить, кроме этого, что для оценки параметра можно предложить не одну, а несколько формул. Так, например, для оценки неизвестного математического ожидания можно взять среднюю арифметическую
можно только с некоторой вероятностью, причем стремление увеличить эту вероятность приводит к увеличению объема выборки. Необходимо отметить, кроме этого, что для оценки параметра можно предложить не одну, а несколько формул. Так, например, для оценки неизвестного математического ожидания можно взять среднюю арифметическую  выборочных данных, или оценку
выборочных данных, или оценку  , где
, где  - максимальное и минимальное выборочное значения, или еще какую – нибудь среднюю. Понятно поэтому, что возникает вопрос о требованиях, которые следует предъявить к статистическим оценкам, чтобы эти оценки были в каком-то определенном смысле надежными (“хорошими”). Эти требования формулируются обычно с помощью следующих трех свойств оценок: состоятельности, несмещенности и эффективности.
- максимальное и минимальное выборочное значения, или еще какую – нибудь среднюю. Понятно поэтому, что возникает вопрос о требованиях, которые следует предъявить к статистическим оценкам, чтобы эти оценки были в каком-то определенном смысле надежными (“хорошими”). Эти требования формулируются обычно с помощью следующих трех свойств оценок: состоятельности, несмещенности и эффективности.
Определение. Оценка  неизвестного параметра
неизвестного параметра  называется состоятельной, если при неограниченном увеличении числа наблюдений n она стремится по вероятности к оцениваемому параметру
называется состоятельной, если при неограниченном увеличении числа наблюдений n она стремится по вероятности к оцениваемому параметру  , т.е. для любого сколь угодно малого числа
, т.е. для любого сколь угодно малого числа  выполняется условие
выполняется условие  при
при  или
или  при
при  .
.
Теорема. Выборочная средняя арифметическая  является состоятельной оценкой неизвестного математического ожидания
является состоятельной оценкой неизвестного математического ожидания  .
.
Доказательство. Пусть признак Х имеет математическое ожидание 
 и дисперсию
и дисперсию 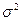 . Для оценки неизвестного математического ожидания
. Для оценки неизвестного математического ожидания  извлекается выборка
извлекается выборка  объема n. Для доказательства теоремы принимаем гипотетическую интерпретацию выборочных данных (ГИВД), т.е. считаем, что в нашем распоряжении имеются n независимых случайных величин Х1,Х2,...,Хn, которые распределены так же, как и признак Х, и, следовательно, имеют одинаковые математические ожидания
объема n. Для доказательства теоремы принимаем гипотетическую интерпретацию выборочных данных (ГИВД), т.е. считаем, что в нашем распоряжении имеются n независимых случайных величин Х1,Х2,...,Хn, которые распределены так же, как и признак Х, и, следовательно, имеют одинаковые математические ожидания  и одинаковые дисперсии
и одинаковые дисперсии  . Тогда средняя арифметическая
. Тогда средняя арифметическая  также оказывается случайной величиной. В теории вероятностей для независимых CB доказано, что
также оказывается случайной величиной. В теории вероятностей для независимых CB доказано, что  . Применяя к случайной величине
. Применяя к случайной величине  неравенство Чебышева, получим:
неравенство Чебышева, получим:
 при
при  ,
,
откуда следует, что выборочная средняя арифметическая  является состоятельной оценкой математического ожидания
является состоятельной оценкой математического ожидания  .
.
Теорема. Выборочная дисперсия S2(n) является состоятельной оценкой генеральной дисперсии 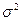 признака Х.
признака Х.
Требование состоятельности оценки должно проверяться в первую очередь, ибо оно отражает практический смысл оценки: при увеличении числа наблюдений оценка должна приближать нас к истинному значению оцениваемого параметра.
С другой стороны, требование состоятельности недостаточно для полной характеристики “хороших” оценок, поскольку это свойство асимптотическое, т.е. проявляется при больших n, до которых на практике обычно не добираются. Кроме этого, в большинстве случаев можно предложить несколько состоятельных оценок одного и того же параметра. Так, величина  является также состоятельной оценкой математического ожидания, если только признак распределен симметрично.
является также состоятельной оценкой математического ожидания, если только признак распределен симметрично.
Определение. Оценка  неизвестного параметра
неизвестного параметра  называется несмещенной, если
называется несмещенной, если 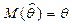 .
.
В предыдущем параграфе было показано, что 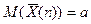 т.е.
т.е. 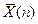 является несмещенной оценкой математического ожидания
является несмещенной оценкой математического ожидания  .
.
Доказано, что  , следовательно,
, следовательно,  является смещенной оценкой генеральной дисперсии
является смещенной оценкой генеральной дисперсии 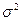 ,- она имеет отрицательное смещение
,- она имеет отрицательное смещение  . Если смещение заранее известно ( как в случае выборочной дисперсии), то его легко устранить, т.е., как говорят, исправить оценку. Так, для оценки генеральной дисперсии
. Если смещение заранее известно ( как в случае выборочной дисперсии), то его легко устранить, т.е., как говорят, исправить оценку. Так, для оценки генеральной дисперсии 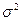 используется исправленная выборочная дисперсия
используется исправленная выборочная дисперсия  :
:

которая, как легко понять, будет уже несмещенной оценкой. Выборочная дисперсия и исправленная выборочная дисперсия отличаются множителем  , который мало отличается от единицы при больших
, который мало отличается от единицы при больших  . Из сказанного следует, что требование несмещенности существенно при малом объеме выборок
. Из сказанного следует, что требование несмещенности существенно при малом объеме выборок  и именно для малых выборок в качестве оценки генеральной дисперсии берут исправленную выборочную дисперсию.
и именно для малых выборок в качестве оценки генеральной дисперсии берут исправленную выборочную дисперсию.
Примеры показывают, что состоятельная оценка может оказаться смещенной, а несмещенная оценка может не быть состоятельной.
Возникает вопрос: из двух оценок неизвестного параметра  какую следует предпочесть: смещенную, но состоятельную или не состоятельную, но несмещенную? Ответить на этот вопрос помогает третье требование к оценкам - эффективность. Представляется достаточно очевидным, что рассматривая несколько оценок неизвестного параметра
какую следует предпочесть: смещенную, но состоятельную или не состоятельную, но несмещенную? Ответить на этот вопрос помогает третье требование к оценкам - эффективность. Представляется достаточно очевидным, что рассматривая несколько оценок неизвестного параметра  , хотелось бы выбрать ту, которая бы имела наименьший разброс относительно оцениваемого параметра
, хотелось бы выбрать ту, которая бы имела наименьший разброс относительно оцениваемого параметра  :
:  . Известно, что мерой разброса оценки
. Известно, что мерой разброса оценки  , как для любой случайной величины, является дисперсия
, как для любой случайной величины, является дисперсия  . Теперь ясно, что если оценка
. Теперь ясно, что если оценка  -смещенная, то дисперсия
-смещенная, то дисперсия 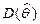 является мерой разброса оценки не относительно оцениваемого параметра
является мерой разброса оценки не относительно оцениваемого параметра  , а относительно
, а относительно  . Поэтому следует предпочитать искать оценки с минимальной дисперсией среди несмещенных оценок. Для несмещенных оценок дисперсия определяется формулой
. Поэтому следует предпочитать искать оценки с минимальной дисперсией среди несмещенных оценок. Для несмещенных оценок дисперсия определяется формулой  .
.
В математической статистике эффективность является решающим свойством оценки. Оценка 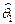 скалярного параметра
скалярного параметра  является более эффективной по сравнению с оценкой
является более эффективной по сравнению с оценкой  , если
, если

Напомним, что если оценки  являются несмещенными, то число
являются несмещенными, то число  есть отношение дисперсий
есть отношение дисперсий  .
.
Оценка  называется эффективной оценкой параметра
называется эффективной оценкой параметра  , если она среди всех оценок этого параметра обладает наименьшей мерой случайного разброса относительно истинного значения параметра
, если она среди всех оценок этого параметра обладает наименьшей мерой случайного разброса относительно истинного значения параметра  .
.
Отметим, что средняя арифметическая 
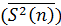 являются эффективными оценками неизвестных матожидания и дисперсии (генеральной средней и генеральной дисперсии).
являются эффективными оценками неизвестных матожидания и дисперсии (генеральной средней и генеральной дисперсии).
6. Интервальные оценки параметров генеральной совокупности.
|
из
5.00
|
Обсуждение в статье: Гипотетическая интерпретация выборочных данных (ГИВД). Точечное оценивание параметров распределений. Требования к точечным оценкам |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

