Отыскание параметров уравнения прямой регрессии

Рассмотрим корреляционную таблицу в общем виде.

Таблица 6. Общий вид корреляционной таблицы

xi yi	x1	x2	.....	xi	.......	xs	итого nyj
y1	n11	n12	.....	n1i	......	n1s	ny1
y2	n21	n22	.....	n2i	......	n2s	ny2
.......	........	.........	........	...........	..........	............	.........
yj	nj1	nj2	.......	nji	.......	njs	nyj
.............	..........	..........	.........	...........	..........	..........	...........
yt	nt1	nt2	.......	nti	........	nts	nyt
Итого nxi Средние	nx1	nx2	……   ……	nxi   …..	……   ……	nxs

Как видно из примеров , некоторые клетки таблицы могут оказаться пустыми, - в таких случаях считаем, что соответствующие частоты равны нулю. В таблице 6. - частоты соответствующих пар переменных . Сумма всех частот дает объем совокупности n:

(9)

при этом

(10)

Из корреляционной таблицы видно, что признак Х принимает значение с частотой , значение с частотой и т.д., следовательно, общая средняя признака Х вычисляется по формуле:

(11)

Аналогично вычисляется общая средняя признака Y:

. (12)

Условные средние находятся следующим образом:

. (13)

Ранее уже было сказано о построении корреляционного поля, т.е. точек с координатами . Предположим, что мы по виду корреляционного поля пришли к выводу о существовании между значениями признаков Х и Y линейной корреляционной зависимости:

. (14)

Естественное желание состоит в том, чтобы параметры и этой функции подобрать так, чтобы суммарное отклонение точек корреляционного поля от прямой было наименьшим. Действительно, если в уравнение (14) последовательно подставлять значения признака Х, то будем получать значения признака Y, которые назовем теоретическими: . Разумеется, теоретические значения , как правило, отличаются от фактических . Математическая задача ставится следующим образом: параметры и уравнения прямой регрессии выбираются такими, чтобы функция принимала наименьшее значение. Заметим, что последняя формула учитывает «вес» каждой точки , т.е. общее число наблюдений, по которым рассчитывалась соответствующая средняя и, таким образом, каждая пара учитывается столько раз, сколько раз она наблюдается в корреляционной таблице. Указанный метод определения параметров уравнения регрессии называется методом наименьших квадратов (МНК).

Итак, функцию двух переменных требуется исследовать на экстремум (минимум). Для этого находим частные производные этой функции и приравнивая их к нулю, получаем так называемую систему нормальных уравнений для определения и :

(15)

Сокращая все члены уравнений на 2 и группируя члены, содержащие и , получим:

(16)

Поделив все члены уравнений на общее число наблюдений n, преобразуем систему к виду:

(17)

Систему (17) можно записать в более компактном виде, если учесть некоторые соотношения, вытекающие из корреляционной таблицы 6. Действительно, соотношения 9 - 13 показывают, что коэффициент при во втором уравнении равен единице. Кроме этого, коэффициент при в первом уравнении и коэффициент при во втором равны . Коэффициент при в первом уравнении представляет собой среднюю арифметическую квадратов значений признака Х, и поэтому обозначается . Преобразуем свободный член второго уравнения и получим, что свободный член второго уравнения равен .

Наконец, доказывается, что свободный член первого уравнения системы равен средней арифметической произведений значений признаков Х и Y которую обозначим . В результате этих преобразований и обозначений система (17) принимает вид

. (18)

Из второго уравнения этой системы находим и подставляем в уравнение регрессии . В результате этого уравнение прямой регрессии получаем в виде: 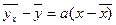, который показывает, что прямая регрессии проходит через точку . Коэффициент обычно обозначают и назы -вают коэффициентом регрессии на , поэтому уравнение будем писать в виде

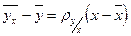(19)

Коэффициент регрессии находим, решая до конца систему (18).

Например, умножим второе уравнение на и сложим с первым. Получим , откуда . Итак, окончательные итоги таковы: уравнение прямой регрессии на имеет вид:

,

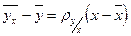коэффициент регрессии находится по формуле

,

где: