 |
Главная |
Уравнения касательной и нормали к графику функции
|
из
5.00
|
Раздел 8. Дифференциальное исчисление функций одной переменной.
1. Производная функции, её геометрический и физический смысл
2. Уравнения касательной и нормали к графику функции.
3. Таблица производных.
4. Основные правила дифференцирования.
5. Связь непрерывности и дифференцируемости.
6. Дифференциал функции.
7. Формула приближённых вычислений значений функций с помощью дифференциала.
8. Основные теоремы дифференциального исчисления
9. Формула Тейлора.
10. Исследование функции с помощью первой производной.
11. Исследование функции с помощью второй производной.
12. Пример полного исследования функции.
Производная функции, её геометрический и физический смысл.
Рассмотрим функцию  , дадим аргументу приращение
, дадим аргументу приращение  получим новое значение функции
получим новое значение функции  В результате функция получит приращение
В результате функция получит приращение 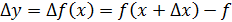 ( х).
( х).
Определение. Производной функции в произвольной точке  называется предел отношения приращения функции в этой точке к приращению аргумента при
называется предел отношения приращения функции в этой точке к приращению аргумента при 
Производная функции  в точке
в точке  обозначается
обозначается  Итак, по определению
Итак, по определению

Пример 1. Найти производную функции 
Решение. По определению 
=  =
=  =
=
= 
Если аргумент интерпретировать как время t движения материальной точки, а путь, пройденный этой точкой изменяется по закону  , то отношение
, то отношение  означает среднюю скорость точки на временном промежутке
означает среднюю скорость точки на временном промежутке 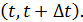 Тогда
Тогда 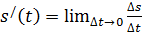 означает мгновенную скорость точки в любой момент времени – в этом состоит физический смысл производной.
означает мгновенную скорость точки в любой момент времени – в этом состоит физический смысл производной.
Поскольку все процессы в природе находятся в движении, в развитии, а характеристикой всякого движения является скорость, то ясно, какое значение в изучении реальных процессов принадлежит производной функции.
Мы часто пользуемся графиками функций, поэтому рассмотрим геометрический смысл производной.
 | |||
 | |||


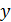











 В
В
 |

|


 A
A
 |


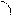


|






 Рис. 1
Рис. 1
Рассмотрим график функции  (рис.1) Возьмём некоторую точку
(рис.1) Возьмём некоторую точку  , вычислим
, вычислим  и покажем на рисунке значение производной в точке
и покажем на рисунке значение производной в точке  . Дадим аргументу приращение
. Дадим аргументу приращение  , получим новое значение аргумента
, получим новое значение аргумента  и вычислим новое значение функции
и вычислим новое значение функции  Имеем две точки на графике:
Имеем две точки на графике:  Проведём секущую
Проведём секущую  , тем самым получится
, тем самым получится  В этом треугольнике
В этом треугольнике
 тогда
тогда  .
.
При  точка
точка  , оставаясь на кривой, стремится к точке
, оставаясь на кривой, стремится к точке  ; секущая
; секущая  становится в пределе касательной к графику функции в точке
становится в пределе касательной к графику функции в точке  Тангенс угла наклона секущей становится тангенсом угла наклона касательной.
Тангенс угла наклона секущей становится тангенсом угла наклона касательной.
Геометрический смысл производной функции в точке  - это тангенс угла наклона касательной к графику функции в этой точке к положительному направлению оси
- это тангенс угла наклона касательной к графику функции в этой точке к положительному направлению оси  (рис.2)
(рис.2)





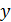
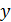



|


 A
A



 |






 0
0 


Рис.2.
Уравнения касательной и нормали к графику функции.
Рассмотрим функцию  и напишем уравнение касательной к графику этой функции в некоторой точке
и напишем уравнение касательной к графику этой функции в некоторой точке  где
где 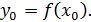 ( см.рис.2)
( см.рис.2)
Воспользуемся уравнением прямой с угловым коэффициентом и опорной точкой: у -  =k(x -
=k(x - 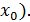 Исходя из геометрического смысла производной
Исходя из геометрического смысла производной  Обозначим это число
Обозначим это число  следовательно, уравнение касательной имеет вид:
следовательно, уравнение касательной имеет вид:  .
.
Нормалью к кривой в точке  называется прямая, перпендикулярная касательной к кривой в этой точке. Условие перпендикулярности двух прямых состоит в том, что произведение их угловых коэффициентов равно – 1. Получаем окончательный вывод:
называется прямая, перпендикулярная касательной к кривой в этой точке. Условие перпендикулярности двух прямых состоит в том, что произведение их угловых коэффициентов равно – 1. Получаем окончательный вывод:
 - уравнение касательной,
- уравнение касательной,
 - уравнение нормали к графику функции
- уравнение нормали к графику функции  в точке
в точке  , где
, где  .
.
Пример 2. Написать уравнения касательной и нормали к графику функции  в точке
в точке 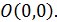
Решение. Воспользуемся уравнениями касательной и нормали - осталось найти  (
( 
 (0). Так как
(0). Так как  (x)=
(x)=  =cosx, то
=cosx, то  (0)=cos0=1. Получаем:
(0)=cos0=1. Получаем: 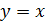 , т.е. биссектриса I-III координатных углов, является касательной графика синуса в начале координат;
, т.е. биссектриса I-III координатных углов, является касательной графика синуса в начале координат;  - уравнение нормали.
- уравнение нормали.
Таблица производных.
Первым непременным условием освоения техники дифференцирования является знание таблицы производных, т.е. производных всех основных элементарных функций. Приводим доказательства.
а)  – показательная функция.
– показательная функция.




|
|
|

Отметим замечательное свойство показательной функции  - она при дифференцировании не меняется. Это свойство является причиной огромного значения этой функции в теоретических исследованиях и практических приложениях.
- она при дифференцировании не меняется. Это свойство является причиной огромного значения этой функции в теоретических исследованиях и практических приложениях.
б)  - логарифмическая функция.
- логарифмическая функция.



|


|
в)  -степенная функция.
-степенная функция.






|

г) 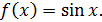





|

Остальные табличные производные доказываются аналогично. Приводим теперь таблицу производных:
1)  ;
;
2)  ;
;  )
)  ;
;
3)  ;
; 
 ;
;
4) 
5)  ;
;
6)  ;
;
7)  ;
;
8) 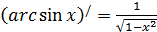 ;
;
9)  ;
;
10)  :
:
11)  .
.
|
из
5.00
|
Обсуждение в статье: Уравнения касательной и нормали к графику функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


