 |
Главная |
Формула приближённых вычислений значений функций с помощью дифференциала
|
из
5.00
|
Мы уже подчёркивали, что дифференциал функции представляет собой главную часть приращения функции, поэтому получаем приближенное равенство  или
или  . Это достаточно хорошо видно на рис.4.
. Это достаточно хорошо видно на рис.4.
Конечно, если  - большое, то разница между
- большое, то разница между  и
и  ощутимая. Но ясно, что чем меньше
ощутимая. Но ясно, что чем меньше  , тем меньше указанная разница и тем оправданнее использование приближённой формулы
, тем меньше указанная разница и тем оправданнее использование приближённой формулы 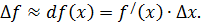 Учитывая
Учитывая
 получим формулу приближённых вычислений значений функции с помощью дифференциала:
получим формулу приближённых вычислений значений функции с помощью дифференциала:

Формула справедлива для любого значения аргумента  На практике выбирают какое-нибудь одно
На практике выбирают какое-нибудь одно  и формула имеет вид:
и формула имеет вид:
 (3)
(3)
Пример 10. Вычислить приближённо с помощью дифференциала число 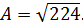
Решение. Число А есть значение функции  в точке х=224. Точка
в точке х=224. Точка  - «неудобная» точка – из этого числа корень«не извлекается», т.е. значение корня не равно целому числу. Поэтому подбираем ближайшую удобную точку
- «неудобная» точка – из этого числа корень«не извлекается», т.е. значение корня не равно целому числу. Поэтому подбираем ближайшую удобную точку  Тем самым определилось приращение аргумента
Тем самым определилось приращение аргумента  Теперь остаётся обратиться к формуле приближённых вычислений (3). Находим f
Теперь остаётся обратиться к формуле приближённых вычислений (3). Находим f 


Подставляем всё найденное в формулу (3):

Основные теоремы дифференциального исчисления
Так называется ряд теорем, появившихся в XVIII веке в трудах французских и немецких математиков и давших начало развитию математического анализа. Рассмотрим несколько основных теорем.
Теорема Ферма. Если функция  дифференцируема на отрезке
дифференцируема на отрезке  и во внутренней точке этого отрезка принимает наибольшее (наименьшее) значение, то производная в этой точке равна нулю.
и во внутренней точке этого отрезка принимает наибольшее (наименьшее) значение, то производная в этой точке равна нулю.
Доказательство: Пусть наибольшее значение достигается в точке  Геометрическое доказательство (геометрический смысл) теоремы очевидно-касательная к графику функции в точке
Геометрическое доказательство (геометрический смысл) теоремы очевидно-касательная к графику функции в точке  параллельна оси абсцисс (рис. 5).
параллельна оси абсцисс (рис. 5).













 |




Рис.5.
Проведём аналитическое доказательство. По определению

Пусть в точке  достигается наибольшее значение. Тогда
достигается наибольшее значение. Тогда  при любом знаке
при любом знаке  .
.
Если 
если 
Поскольку  число, то два неравенства
число, то два неравенства  выполняются при
выполняются при 

Теорема Лагранжа. Если функция  дифференцируема на отрезке
дифференцируема на отрезке  , то внутри отрезка найдётся по крайней мере одна точка с такая, для которой имеет место формула
, то внутри отрезка найдётся по крайней мере одна точка с такая, для которой имеет место формула 




 Рассмотрим геометрический смысл формулы Лагранжа
Рассмотрим геометрический смысл формулы Лагранжа 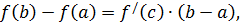 которую запишем в виде
которую запишем в виде  .
.
 В
В


 А
А  М
М
|
|

|
|
|




На рис. 6  тогда
тогда  - из прямоугольного треугольника
- из прямоугольного треугольника  . Далее мысленно передвигаем секущую
. Далее мысленно передвигаем секущую  параллельно самой себе до тех пор, пока она не станет касательной – абсцисса точки касания и есть
параллельно самой себе до тех пор, пока она не станет касательной – абсцисса точки касания и есть  т.к.
т.к. 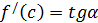 .
.
Формула Тейлора.
В общем виде постановка задачи формулируется следующим образом. Имеется функция  и по некоторым причинам её исследование затруднительно. Поэтому её желательно заменить другой, «близкой к данной». Понятие «близкая» уточняется в каждом конкретном случае.
и по некоторым причинам её исследование затруднительно. Поэтому её желательно заменить другой, «близкой к данной». Понятие «близкая» уточняется в каждом конкретном случае.
В нашем случае пусть имеется функция  , которую мы желаем заменить многочленом
, которую мы желаем заменить многочленом
 (4)
(4)
степени 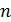 , записанным по степеням
, записанным по степеням 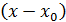 , где
, где  - некоторое число. Коэффициенты
- некоторое число. Коэффициенты  этого многочлена требуется подобрать такими, чтобы выполнялись условия
этого многочлена требуется подобрать такими, чтобы выполнялись условия
 (5)
(5)
Условия (5) и являются конкретным уточнением понятия «близкие» функции. Они требуют, чтобы в точке  совпадали значения многочлена
совпадали значения многочлена  и функция
и функция  и их производные до
и их производные до  го порядка включительно. Как видим, у многочлена надо найти
го порядка включительно. Как видим, у многочлена надо найти  коэффициент
коэффициент  , и для этого имеется
, и для этого имеется  равенств в формуле (5). Итак, реализуем условия (5).
равенств в формуле (5). Итак, реализуем условия (5).
Во-первых, находим  , т.е. в формулу (4) подставляем
, т.е. в формулу (4) подставляем  , все скобки обращаются в ноль, получаем
, все скобки обращаются в ноль, получаем  Из первого условия формулы
Из первого условия формулы 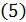 получаем
получаем  .
.
Далее последовательно находим производные многочлена  , подставляем
, подставляем  и используем соответствующее условие формулы (5).
и используем соответствующее условие формулы (5).
















 .
.



 Нетрудно видеть, что
Нетрудно видеть, что 
 Намечается закономерность
Намечается закономерность

Доказано, что эта закономерность действительно имеет место. Для придания полученным формулам более компактный вид введём следующее определение.
Произведение всех натуральных чисел от 1 до 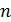 обозначается
обозначается 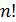 и называется эн - факториал:
и называется эн - факториал: 
Отметим, что сомножитель 1 поставлен не только «для красоты»,- эн – факториал содержит эн - сомножителей. Из определения следует, что  Более того, договорились считать
Более того, договорились считать 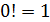 . Возвратимся к формулам для коэффициентов, для которых получаем общий вид:
. Возвратимся к формулам для коэффициентов, для которых получаем общий вид: 
Таким образом, получаем искомый многочлен

Многочлен  , записанный в виде (6), называется многочленом Тейлора для функции
, записанный в виде (6), называется многочленом Тейлора для функции  . Мы уже говорили, что имеет место приближённое равенство
. Мы уже говорили, что имеет место приближённое равенство  , т.е.
, т.е.


Формула (7) называется разложением функции  по формуле Тейлора. Как видим, эта формула является приближённой. Разность
по формуле Тейлора. Как видим, эта формула является приближённой. Разность  называется остаточным членом формулы Тейлора: тогда получим
называется остаточным членом формулы Тейлора: тогда получим 
Существуют разные формы остаточного члена  С помощью теоремы Лагранжа доказано, что между точками
С помощью теоремы Лагранжа доказано, что между точками  и
и  существует точка
существует точка  такая, что
такая, что
 (8)
(8)
Формула (8) называется остаточным членом формулы Тейлора в форме Лагранжа. Подчеркнём, что  в виде (8) похож на следующий,
в виде (8) похож на следующий,  - й член формулы Тейлора, с той лишь разницей, что вместо
- й член формулы Тейлора, с той лишь разницей, что вместо  берётся точка
берётся точка  , о которой известно лишь то, что она существует, где то между точками
, о которой известно лишь то, что она существует, где то между точками  . Итак, мы получили формулу Тейлора с остаточным членом в формуле Лагранжа:
. Итак, мы получили формулу Тейлора с остаточным членом в формуле Лагранжа:


Заметим, что если ограничиться 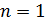 , то получим
, то получим 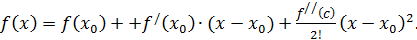
Видим, что первые два слагаемых дают приближённое вычисление значения функций с помощью дифференциала, но теперь мы имеем возможность оценить погрешность наших вычислений.
|
из
5.00
|
Обсуждение в статье: Формула приближённых вычислений значений функций с помощью дифференциала |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

