 |
Главная |
Определение проектных отметок на вертикальных кривых
|
из
5.00
|
Для определения проектных отметок на вертикальных кривых сначала вписываем вертикальную кривую по следущей методике:
1) Определяют алгебраическую разность уклонов Δi двух смежных участков, учитывая правило знаков по формуле:
Δi=i1-i2 (3.3)
При движении вверх, уклон принимается со знаком + и при движении вниз уклон принимается со знаком -.
2) Отрезки проектной линии различных уклонов для обеспечения плавного движения автомобиля, сопрягают вертикальными кривыми. Вертикальные кривые бывают вогнутыми и выпуклыми. Радиус вертикальной кривой назначается в зависимости от категории дороги и условий проложения проектной линии.
3) Определяют длину вертикальной кривой в зависимости от радиуса в соответствии с технической категорией дороги по формуле:
К=Δi·R, м (3.4)
4) Местоположение середины кривой (СК) определяют по формуле:
h=(К/2)2/2R (3.5)
5) От точки перелома проектной линии (С) в обе стороны откладывают по половине кривой К/2 и определяют местоположение начала кривой (НК) и конца вертикальной кривой (КК);
6) Плавно соединяем точки начала, середины и конца вертикальной кривой (рис. 3.3);
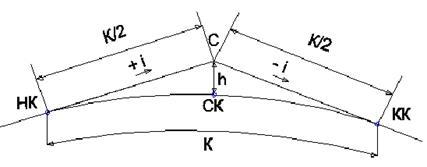
Рисунок 3.3 Схема к вписанию вертикальной кривой
Проектные отметки в пределах вертикальной кривой определяются в первую очередь в вершине кривой (ВК).
Отметка в ВК на вертикальной выпуклой кривой (рис. 3.4) определяется по формуле:
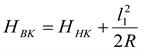 (3.7)
(3.7)
где: l1 - расстояние от начала кривой (НК) до вершины кривой (ВК).
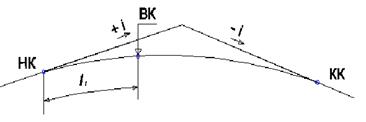
Рисунок 3.4 Схема к определению расстояния до вершины вертикальной выпуклой кривой и ее высотной отметки
Отметка в вершине кривой (ВК) на вертикальной вогнутой кривой (рис. 3.5).определяется по формуле:
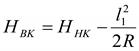 , м (3.8)
, м (3.8)
где: l1 - расстояние от начала кривой (НК) до вершины кривой (ВК).
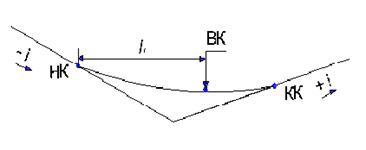
Рисунок 3.5 Схема к определению расстояния до вершины вертикальной вогнутой кривой и ее высотной отметки
Отметка в любой точке К в пределах вертикальной выпуклой кривой (рис. 3.6) определяются по формуле:
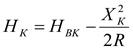 , м (3.9)
, м (3.9)
где: Хк - расстояние от ВК до искомой точки (К), м
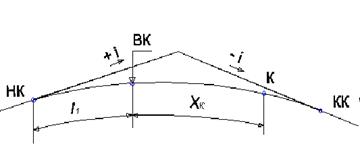
Рисунок 3.6 Схема к определению проектных отметок в любой точке на вертикальной выпуклой кривой
Высотные отметки в пределах вертикальной вогнутой кривой определяется (рис. 3.7):
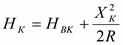 (3.10)
(3.10)
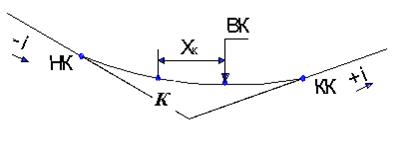
Рисунок 3.7 Схема к определению проектных отметок в любой точке на вертикальной вогнутой кривой
Если один из сопрягаемых отрезков проектной линии имеет i = 0, то вершина выпуклой вертикальной кривой находится на горизонтальном участке прямой в точке НК или КК.
а)
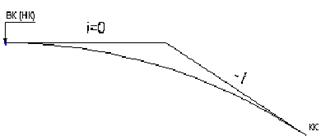
б)

Рисунок 3.8 Схема к определению положения вершины вертикальной кривой при уклоне одного из участков, равном 0
Если вогнутая вертикальная кривая сопрягает прямые линии с уклонами одинакового знака (одного направления), но с различными абсолютными значениями, то вершина кривой располагается, за пределами кривой (на расстоянии Х от начала кривой НК или конца кривой КК).
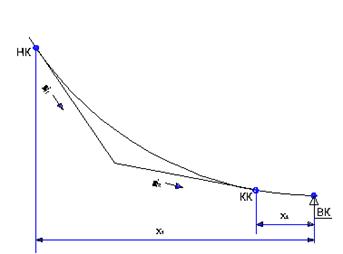
Рисунок 3.9 Схема к определению положения вершины кривой (ВК) на вертикальной вогнутой кривой в случае одинакового направления уклонов двух смежных участков
Если выпуклая вертикальная кривая сопрягает прямые линии с уклонами одинакового знака (одного направления), но с различными абсолютными значениями, то вершина кривой располагается за пределами на расстоянии Х от НК или КК.
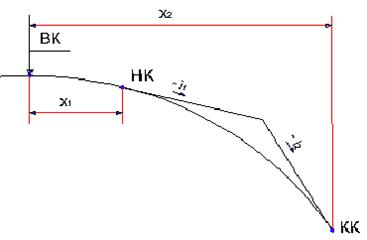
Рисунок 3.10 Схема к определению положения вершины кривой (ВК) на вертикальной выпуклой кривой в случае одинакового направления уклонов двух смежных участков
X1 =i1 ·R (3.11)
X2=i2 ·R (3.12)
По высотным отметкам, вычисленными на плюсовых точках, пикетах и в точках ВК, НК, КК вертикальных кривых, на продольном профиле вычерчивается красной тушью проектная линия. При этом пользуются прозрачными шаблонами. Проектная линия вычерчивается толщиной в 2 раза толще линии поверхности земли и сетки продольного профиля.
|
из
5.00
|
Обсуждение в статье: Определение проектных отметок на вертикальных кривых |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

