Вычисление интеграла от аналитической функции

Интеграл , вообще говоря, зависит от пути интегрирования. Условием независимости интеграла от пути интегрирования является аналитичность подынтегральной функции.

Важную роль в теории функций комплексного переменного играет интегральная теорема Коши. Приведем две формулировки теоремы для одно- и многосвязной областей.

Пусть кусочно-гладкая замкнутая кривая, будем ее называть замкнутым контуром.

Теорема Коши (для односвязной области). Пусть функция аналитична в односвязной области , тогда для любого замкнутого контура (рис.5.1) имеет место равенство

. (5.4)

Теорема Коши (для многосвязной области).Пусть аналитична в многосвязной области , ограниченной внешним контуром и внутренними контурами . Тогда имеет место равенство

(5.5)

при условии, что интегрирование по всем контурам производится против часовой стрелки (рис.5.2).

Как следствие последней теоремы (для двусвязной области) следует отметить утверждение: если аналитична в области всюду, кроме , то

, (5.6)

где и произвольные контуры в , содержащие особую точку (рис.5.3).

Рис.5.1

Рис.5.2

Для аналитической функции имеет место формула Ньютона-Лейбница

, (5.7)

где первообразная для , т.е. . Этой формулой можно пользоваться для вычисления интеграла вдоль пути, лежащего в односвязной области, где аналитична, если известна первообразная для .

Рис.5.3

Техника нахождения неопределенных интегралов в комплексном анализе та же, что и в действительном, таблица основных интегралов в обоих случаях одинакова.

Интегральная формула Коши

Если аналитична в области , и контур, охватывающий точку , то имеют место следующие формулы:

, (5.8)

(5.9)

(контур может быть объединением контуров (см. рис.5.2)).

Формула (5.8) называется интегральной формулой Коши, а интеграл в правой части (5.8) – интегралом Коши. Интегральная формула Коши позволяет находить значение аналитической функции в любой точке, лежащей внутри области , если известны значения этой функции на контуре , ограничивающем . Если точка лежит вне области , то интеграл Коши равен нулю в силу теоремы Коши, так как в этом случае подынтегральная функция является аналитической в области .

Формулы (5.8) и (5.9) могут служить для вычисления интегралов по замкнутым контурам.

УПРАЖНЕНИЯ

70. Вычислить интеграл по линиям, соединяющим точки и

а) по прямой, б) по параболе (рис.5.4).

Рис.5.4

Решение. Функция не является аналитической (проверьте!), поэтому вычисление интеграла возможно как по формуле (5.2), так и по формуле (5.3). Найдем действительную и мнимую части подынтегральной функции По формуле (5.2) имеем .

а) Уравнение отрезка прямой, проходящей через точки и , значит .

Тогда получаем

.

б) 1-й способ. Уравнение дуги параболы: , значит, и

2-й способ. Воспользуемся формулой (5.3). Параметрические уравнения параболы имеют вид , а в комплексной форме - . Находим и

.

71. Вычислить интеграл .

Решение. Так как аналитична всюду, то по формуле Ньютона-Лейбница (5.7) имеем

.

72. Вычислить интеграл .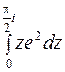

Решение. Функции и являются аналитическими всюду. Применяя формулу интегрирования по частям, получим

.

73. Вычислить интеграл 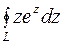по контуру .

Решение. Так как аналитична всюду и контур интегрирования замкнутый, то в силу теоремы Коши (5.4) .

74. Вычислить , где:

а) окружность 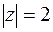. б) окружность .

Решение. а) Функция аналитична в замкнутом круге , поэтому по теореме Коши .

б) Воспользуемся интегральной формулой Коши (5.8), положив . Функция аналитична в круге , а точка лежит в этом круге. Поэтому

.

75. Вычислить интеграл .

Решение. Внутри области, ограниченной окружностью находится одна точка , в которой знаменатель дроби обращается в нуль.

Для применения формулы (5.8) интеграл перепишем в виде .

Здесь функция является аналитической в круге , а точка внутренняя точка круга, поэтому имеем

.

76. Вычислить интеграл .

Рис.5.5

Решение. В круге функция 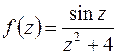аналитическая всюду, кроме точек и . Вырежем из данного круга области и , ограниченными любыми не пересекающими замкнутыми контурами и , причем и (рис. 5.5). Тогда в силу теоремы Коши для многосвязной области (формула (5.5)) имеем

. В качестве и мож-

но взять любые контуры, в частности окружности. Пусть 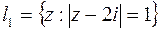и (рис. 5.5). Каждый из интегралов и можно вычислить по интегральной формуле Коши

;

.

Таким образом,

.

77. Вычислить интеграл , где произвольный замкнутый контур, однократно обходящий точку в положительном направлении.

Решение. Внутри контура подынтегральная функция является аналитической всюду, кроме точки . Для вычисления интеграла воспользуемся формулой (5.9), выделив аналитическую в указанной области функцию , полагая . Так как , то в соответствии с (5.9) .