 |
Главная |
ОРИГИНАЛ И ИЗОБРАЖЕНИЕ
|
из
5.00
|
Операционное исчисление является одной из глав современного математического анализа. Интегральное преобразование Лапласа и построенное на его базе операционное исчисление – эффективный аппарат решения дифференциальных уравнений (как обыкновенных, так и в частных производных), дифференциально разностных и интегральных уравнений, к которым приводятся задачи электротехники, радиотехники, электроники, теории автоматического регулирования, теплотехники, механики и других областей науки и техники. Заметим, что операционное исчисление строится и на других преобразованиях, например, Фурье, Ханкеля, Меллина и т.д.
Идея применения операционного метода заключается в следующем. Пусть требуется найти функцию  из некоторого уравнения, содержащего эту функцию под знаком производных и интегралов. От искомой функции
из некоторого уравнения, содержащего эту функцию под знаком производных и интегралов. От искомой функции  (ее называют оригиналом) переходят к другой функции
(ее называют оригиналом) переходят к другой функции 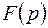 (ее называют изображением), являющейся результатом преобразования
(ее называют изображением), являющейся результатом преобразования  . В соответствии с правилами операционного исчисления операции над оригиналом заменяют соответствующими операциями над изображением, которые являются более простыми; например, дифференцированию
. В соответствии с правилами операционного исчисления операции над оригиналом заменяют соответствующими операциями над изображением, которые являются более простыми; например, дифференцированию  соответствует умножение
соответствует умножение 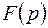 на
на 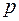 , интегрированию–деление на р и т.д. Это позволяет перейти от сложного уравнения относительно
, интегрированию–деление на р и т.д. Это позволяет перейти от сложного уравнения относительно  к более простому уравнению относительно
к более простому уравнению относительно 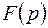 , называемому операторным; например, от дифференциального уравнения–к алгебраическому. Решив операторное уравнение, от изображения
, называемому операторным; например, от дифференциального уравнения–к алгебраическому. Решив операторное уравнение, от изображения 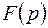 переходят к оригиналу
переходят к оригиналу  – искомой функции. Решение задачи операционным методом, таким образом, связано с двумя этапами; нахождением изображения искомого решения и обратным переходом к оригиналу.
– искомой функции. Решение задачи операционным методом, таким образом, связано с двумя этапами; нахождением изображения искомого решения и обратным переходом к оригиналу.
Применение операционного метода можно сравнить с логарифмированием, которое позволяет сложные действия над числами заменить более простыми действиями над их логарифмами, после чего от найденного логарифма снова переходят к искомому числу. Здесь роль оригиналов играют числа, а роль изображений – их логарифмы.
1.1. Оригинал и изображение
Пусть  – действительная функция действительного аргумента
– действительная функция действительного аргумента  , определенная при любых
, определенная при любых  .
.
Определение. Будем называть оригиналом функцию  , если она удовлетворяет следующим условиям.
, если она удовлетворяет следующим условиям.
1.  – кусочно-непрерывная функция при
– кусочно-непрерывная функция при  ; это значит, что она или непрерывна, или имеет точки разрыва первого рода, число которых конечно на любом конечном интервале;
; это значит, что она или непрерывна, или имеет точки разрыва первого рода, число которых конечно на любом конечном интервале;
2. 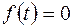 при
при  ;
;
3.  с возрастанием
с возрастанием  может возрастать, но не быстрее некоторой показательной функции. Это означает, что существуют такие числа
может возрастать, но не быстрее некоторой показательной функции. Это означает, что существуют такие числа 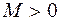 и
и  что для всех
что для всех  выполняется
выполняется  , число
, число 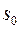 называется показателем роста функции
называется показателем роста функции  . (Для ограниченных функций можно принять
. (Для ограниченных функций можно принять  ).
).
Рассмотрим эти условия несколько подробнее. Условия 1 и 3 выполняются для большинства функций, отвечающих физическим процессам, в которых t понимается как время. Условие 2 оправдано тем, что при изучении процесса безразлично, как ведут себя рассматриваемые функции до некоторого начального момента времени, который, разумеется, можно принять за момент  .
.
В связи с условием 2 в дальнейшем изложении, где это потребуется, будем записывать для краткости лишь то выражение  , которое она имеет для
, которое она имеет для  , подразумевая, что для
, подразумевая, что для  . Например, запись
. Например, запись  должна пониматься так:
должна пониматься так:  .
.
Аналогично, если дано выражение  , где
, где  , то оно имеет место лишь для
, то оно имеет место лишь для  , тогда как для
, тогда как для  функция
функция  .
.
Заметим, что если функция  не удовлетворяет хотя бы одному из указанных трех условий, то она не является оригиналом. Так, для функции
не удовлетворяет хотя бы одному из указанных трех условий, то она не является оригиналом. Так, для функции  нарушено условие 1 (в точке
нарушено условие 1 (в точке  она терпит разрыв второго рода), для функции
она терпит разрыв второго рода), для функции  не выполняется условие 3 (она растет быстрее показательной функции); поэтому эти функции не могут быть оригиналами.
не выполняется условие 3 (она растет быстрее показательной функции); поэтому эти функции не могут быть оригиналами.
Заметим также, что необязательно считать оригинал  действительной функцией. Функция
действительной функцией. Функция  может быть и комплексно-значной, т.е. иметь вид
может быть и комплексно-значной, т.е. иметь вид  . При этом действительная и мнимая части
. При этом действительная и мнимая части  и
и  должны быть оригиналами, т.е. удовлетворять условиям 1, 2, 3.
должны быть оригиналами, т.е. удовлетворять условиям 1, 2, 3.
Определение. Изображением функции  – оригинала–называется функция
– оригинала–называется функция 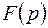 комплексного переменного
комплексного переменного  , определяемая интегралом
, определяемая интегралом
 . (1.1)
. (1.1)
Несобственный интеграл в правой части равенства (1.1), называемый интегралом Лапласа, зависит от параметра 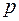 .
.
Таким образом, функции  действительного переменного
действительного переменного  поставлена в соответствие функция
поставлена в соответствие функция 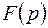 комплексного переменного
комплексного переменного 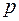 .
.
Соотношение (1.1) осуществляет преобразование одной функции в другую. Операцию перехода от оригинала  к изображению
к изображению 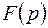 в соответствии с формулой (1.1) называют преобразованием Лапласа, или прямым преобразованием Лапласа.
в соответствии с формулой (1.1) называют преобразованием Лапласа, или прямым преобразованием Лапласа.
Тот факт, что 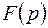 есть изображение (говорят также, изображение по Лапласу), символически записывают так:
есть изображение (говорят также, изображение по Лапласу), символически записывают так:
 .
.
Отыскание оригинала  по изображению
по изображению  называют обращением преобразования Лапласа, или обратным преобразованием Лапласа; его обозначают символом
называют обращением преобразования Лапласа, или обратным преобразованием Лапласа; его обозначают символом  .
.
Условились обозначать оригиналы малыми буквами  а их изображения – соответствующими заглавными буквами
а их изображения – соответствующими заглавными буквами 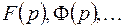 или теми же буквами, что и оригиналы, но снабжать их черточками сверху:
или теми же буквами, что и оригиналы, но снабжать их черточками сверху:  .
.
1.2. Примеры вычисления изображений
Приведем примеры вычисления изображения по Лапласу, исходя из его определения.
1.2.1. Функция Хевисайда и ее изображение.
 Рис.1.1
Рис.1.1
| Функция, определяемая следующим образом:  называется единичной функцией или функцией Хевисайда. График ее изображен на рис. 1.1. Очевидно, эта функция является оригиналом, ибо она удовлетворяет условиям 1, 2, 3. называется единичной функцией или функцией Хевисайда. График ее изображен на рис. 1.1. Очевидно, эта функция является оригиналом, ибо она удовлетворяет условиям 1, 2, 3.
|
Найдем изображение функции Хевисайда по формуле (1.1), полагая в ней 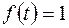 :
:
 .
.
Последнее заключение можно сделать только, в том случае, когда  . Покажем, что это выполняется. По формуле Эйлера имеем:
. Покажем, что это выполняется. По формуле Эйлера имеем:
 .
.
Тогда

так как  при
при  .
.
Следовательно, когда

 .
.
Таким образом, интеграл Лапласа для единичной функции сходится при  и ее изображением является функция
и ее изображением является функция 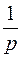 . Итак,
. Итак,
 . (1.2)
. (1.2)
В связи с введением функции Хевисайда заметим следующее. Когда идет речь о некоторой функции – оригинале, например,  ,
,  и т.п., то всегда подразумевается, что
и т.п., то всегда подразумевается, что

 и т.п.
и т.п.
С помощью функции  можно записать:
можно записать:
 .
.
Роль множителя состоит в том, что он «гасит» (обращает в нуль) функцию при  . Однако для сокращения записи множитель
. Однако для сокращения записи множитель  иногда опускают.
иногда опускают.
1.2.2. Изображение показательной функции.
Функция 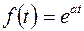 , где
, где  любое комплексное число. Согласно нашей договоренности
любое комплексное число. Согласно нашей договоренности 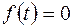 при
при  . Условия 1 и 3 выполняются, причем в силу
. Условия 1 и 3 выполняются, причем в силу  можно положить
можно положить  ,
,  . Следовательно,
. Следовательно,  оригинал. По формуле (1.1) найдем
оригинал. По формуле (1.1) найдем


Это имеет место, если только  . Последнее же выполняется, как было показано в предыдущем примере, когда
. Последнее же выполняется, как было показано в предыдущем примере, когда  , иначе
, иначе  . Таким образом,
. Таким образом,
 . (1.3)
. (1.3)
|
из
5.00
|
Обсуждение в статье: ОРИГИНАЛ И ИЗОБРАЖЕНИЕ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

