Критические операции и резервы времени у некритических операций

Критерием определения критических операций будет совпадение наиболее ранних и поздних сроков: Задержка любой из этих операций может приводить к срыву срока проекта в целом, поэтому у них резервы времени равны нулю.

Для остальных, некритических, операций рассчитываются полный и свободный временные резервы. Первый определяет время, на которое можно задержать операцию, без срыва проекта, второй — без сдвига любой последующей операции.

Полный резерв времени операции (TF) равен разнице наиболее позднего срока начала (LS) и наиболее раннего срока начала (ES) или разнице наиболее позднего срока окончания (LF) и наиболее раннего срока окончания (EF) текущей операции.

^.

Для определения свободного резерва времени операции (FF_i) необходимо знать все наиболее ранние сроки (ES_i+1) операций, непосредственно следующих за текущей. Нужно выбрать минимальный из этих сроков и вычесть из него наиболее ранний срок окончания текущей операции (EF_i), полученная разница и есть свободный резерв.

^.

Расчет показателей проекта (по данным табл. 4.1)

Итак, воспользуемся приведенными формулами и определим критические операции и резервы времени. Вначале рассчитаем наиболее ранние сроки начала и окончания операций (табл. 8).

Таблица 8 - Расчет наиболее ранних сроков начала и окончания операций

Операция	Продолжительность	Наиболее ранний срок начала	Наиболее ранний срок окончания	Комментарий
A			0 + 8 = 8	ES0=0
B			0 + 10 = 10	ES0=0
C			0 + 6 = 6	ES0=0
D			10 + 8 = 18	Нельзя начать, пока не завершены A и B
E			10 + 9 = 19	Нельзя начать, пока не завершены B и C
F			14 + 6 = 20	Нельзя начать, пока не завершена C
G			14 + 19 = 33	Нельзя начать, пока не завершены D и E
H			33 + 6 = 39	Нельзя начать, пока не завершены F и G

 

Рассчитав наиболее ранние сроки начала и окончания, определив срок осуществления проекта — , мы можем перейти к расчету наиболее поздних сроков начала и окончания работ (табл. 4.3).

Критический путь в данном случае состоит из следующих операций: B-E-G-H. Соответственно резервы времени, как полный, так и свободный у них равны нулю. Для остальных операций рассчитаем соответствующие полные и свободные резервы времени:

для операции A:

, ;

для операции C:

, ;

для операции D:

, ;

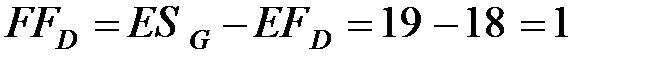для операции F:

, .

Таблица 9 - Расчет наиболее поздних сроков начала и окончания операций

Операция	Продолжительность	Наиболее поздний срок окончания	Наиболее поздний срок начала	Комментарий
H			39 — 6 = 33	LFf = EFf
G			33 — 14 = 19	G нужно завершить до наступления наиболее позднего срока начала H
F			33 — 14 = 19	F нужно завершить до наступления наиболее позднего срока начала H
E			19 — 9 = 10	E нужно завершить до наступления наиболее позднего срока начала G
D			19 — 8 = 11	D нужно завершить до наступления наиболее позднего срока начала G
C			10 — 6 = 4	C нужно завершить до наименьшего из наступления наиболее поздних сроков начала E и F
B			10 — 10 = 0	B нужно завершить до наименьшего из наступления наиболее поздних сроков начала E и D
A			11 — 8 = 3	A нужно завершить до наступления наиболее позднего срока начала D

 

Стрелочные сети. В данном виде сетей для представления операции используется стрелка (ориентированная дуга), направление которой соответствует процессу реализации проекта во времени. Отношение упорядочения между операциями задается с помощью событий. Событиеопределяется как момент времени, когда завершаются одни операции и начинаются другие. Начальная и конечная точки любой операции описываются парой событий, которые называют начальным событием и конечным событием. Операции, выходящие из некоторого события, не могут начаться, пока не будут завершены все операции, входящие в это событие. По принятой терминологии каждая операция представляется ориентированной дугой, а каждое событие — узлом (вершиной).

На рис. 5 а приведен пример графического изображения операции (i,j) с начальным событием i и конечным j. На рис. 5 б показан другой пример, из которого видно, что для возможности начала операции (3,4) требуется завершение операций (1,3) и (2,3). Протекание операций во времени задается путем нумерации событий, причем номер начального события всегда меньше номера конечного.

 

а)

б)

Рисунок 5

Приведем правила построения сетевой модели.

Правило 1. Каждая операция в сети представляется одной дугой (стрелкой).

Правило 2. Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями.

Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно (рис. 6 а). Чтобы исключить такую ситуацию вводится фиктивная операция, которая обозначается пунктирной стрелкой.

 

D

B

A

А

В

А

A

D

B

A

D

B

B

D

а)

б)

Рисунок 6

Рис. 6 б иллюстрирует различные варианты введения такой фиктивной операции D. В результате операций А и В определяются теперь однозначно парой событий, отличающихся либо номером начального, либо номером конечного события. Заметим, что фиктивные операции не требуют затрат ни времени, ни ресурсов.

Фиктивные операции позволяют также правильно отображать логические связи, которые без их помощи нельзя задать на сети. Предположим, что в некотором проекте операции А и В должны непосредственно предшествовать С, а операции Е непосредственно предшествует только В. На рис. 7 а эти условия отражены неверно, так как, хотя упорядочения между А, В и С показаны правильно, из этого фрагмента следует, что операции Е должны непосредственно предшествовать обе операции А и В. Правильное представление указанных условий дает фрагмент (б), в котором используется фиктивная операция D. Поскольку на операцию D не затрачиваются ни время, ни ресурсы, заданные отношения упорядочения выполняются.

A

B

A

E

C

B

C

E

D

а)

б)

Рисунок 7

Правило 3. При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы.

а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?

б) Какие операции должны непосредственно следовать после завершения данной операции?

в) Какие операции могут выполняться одновременно с рассматриваемой?

Для правильной нумерации событий используем следующий алгоритм:

Шаг 1. Присвоить событию, в которое не входит ни одной дуги, начальный номер.

Шаг 2. Присвоить следующий номер любому неперенумерованному событию, для которого все предшествующие события перенумерованы.

Повторять шаг 2 до тех пор, пока все события не будут перенумерованы.

События сети должны быть пронумерованы таким образом, что возрастание номеров соответствует ходу выполнения проекта.

Расчет параметров сетевого графика. Расчет сетевой модели ведется по следующим параметрам:

1. Критический путь (события и работы, лежащие на критическом пути) и продолжительность критического пути t_кр.

Путь — это непрерывная последовательность работ от исходного до завершающего события сетевой модели. Путь с наибольшей продолжительностью называется критическим.

Работы, составляющие критический путь, на сетевом графике обозначаются двойными стрелками.

2.Параметры событий:

2.1. Ранний срок свершения события определяет срок, необходимый для выполнения всех работ, предшествующих данному событию. Ранний срок свершения начального события i принимается равным нулю: = 0. Ранние сроки свершения всех последующих событий определяются в строгой последовательности по возрастающим номерам событий. Для определения раннего срока свершения любого события j рассматриваются все работы, входящие в это событие; по каждой работе определяется ранний срок свершения конечного события как сумма раннего срока свершения начального события работы и продолжительности этой работы t_i,j. Из полученных значений выбирается максимальное, что и представляет собой ранний срок свершения события j:

.

2.2. Поздний срок свершения события. Поздний срок свершения завершающего события С принимается равным его раннему сроку свершения, т. е. t_nc = t_pc = t_кр. Расчет поздних сроков свершения всех остальных событий ведется в обратной последовательности, по убывающим номерам событий. Для определения позднего срока свершения события i рассматриваются все работы, выходящие из i-го события. По каждой работе ведется расчет позднего срока свершения начального события t_pi как разность между поздним сроком свершения конечного события этой работы t_pj и продолжительностью данной работы t_ij. Из полученных значений выби­рается минимальное время, которое и определяет поздний срок свер­шения i-го события:

.

2.3. Резерв времени i-го события определяется разностью между поздним и ранним сроками его свершения:

.

Рассчитанные параметры событий целесообразно разместить насетевом графике следующим образом (см. рис. 8).

 

 

Ri tрi tпi i

Rj tрj tпj J

tij

 

Рисунок 8 - Размещение на сетевом графике
исходных данных и расчетных параметров

 

3. Параметры работ.

В качестве параметров работ определяются:

а) наиболее ранний из возможных сроков начала работы:

;

б) наиболее ранний срок окончания работы:

;

в) наиболее поздний срок начала работы:

;

г) наиболее поздний срок окончания работы:

;

д) полный резерв времени работы, т. е. время, на которое можно увеличить продолжительность данной работы, не изменяя при этом продолжительности критического пути:

;

е) свободный резерв времени работы, то есть время, на которое можно увеличить продолжительность работы, не изменяя ранних сроков начала последующих работ:

.

Результаты расчетов параметров работ целесообразно отразить в виде табл. 10.

Таблица 10

Код работы i — j	Полный резерв	Свободный резерв

 

В вершинном графике нет событий, так как там только операции, а в сетевом есть и события — в узлах, и работы — в дугах. Если мы в сетевом графике захотим рассуждать в терминах работ, то можно воспользоваться следующими простыми формулами перевода времен событий во времена операций:

; ; ; .

Ниже приведен пример планирования хода реализации проекта с использованием стрелочного сетевого графика. Исходные данные для расчетов представлены в табл. 11.

Таблица 11 - Исходные данные для построения и расчета сетевого графика

Работа (операция)	Предшествующая работа	Продолжительность работы, дни	Число исполнителей, чел.
А	-
B	-
C	A,B
D	A,B
E	B
F	C

 

Сетевой график и карта проекта, построенные в соответствии с заданием, приведены на рис. 9.

Критический путь проходит по событиям 1–2–3–5 и равен
13 дням, что означает, что для выполнения всего комплекса работ, указанного в задании, потребуется 13 дней. Результаты расчета параметров событий отражены в табл. 12. Результаты расчета параметров работ приведены в табл. 13.

 

Таблица 12 - Результаты расчета параметров событий

Параметры	Событие
Ранний срок свершения
Поздний срок свершения
Резерв времени

 

Таблица 13 - Результаты расчета параметров работ

Параметры	Работы
1-2	1-3	3-4	3-5	2-5	4-5
Полный резерв времени работы
Свободный резерв времени работы

 

Рисунок 9 - Карта проекта