 |
Главная |
Аналитическое выравнивание динамического ряда. Построение модели тренда
|
из
5.00
|
Аналитической выравнивание динамического ряда имеет своей целью получение некоторой математической модели, которая наилучшим образом в заданном смысле выражает динамику анализируемого явления.
В качестве моделей тренда используются полиномы различных степеней, экспоненты и логарифмические кривые.
Процесс выравнивания динамического ряда состоит из двух основных этапов:
- выбор типа кривой (формы), которая наилучшим образом подходит;
- определения численных значений (оценка) параметров кривой.
Вопрос о выборе типа кривой является основным при выравнивании ряда. При всех прочих равных условиях ошибка в решении этого вопроса оказывается более значимой по своим последствиям, чем ошибка, связанная со статистическим оцениванием параметров.
Правильная идентификация тренда важна при построении прогноза.
Рассмотрим наиболее используемые типы уравнений тренда:
1. Линейная форма тренда:
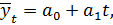
где 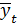 – уровень ряда, полученный в результате выравнивания по прямой;
– уровень ряда, полученный в результате выравнивания по прямой; 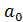 – начальный уровень тренда;
– начальный уровень тренда; 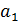 – средний абсолютный прирост, константа тренда.
– средний абсолютный прирост, константа тренда.
Для линейной формы тренда характерно равенство так называемых первых разностей (абсолютных приростов) и нулевые вторые разности, т. е. ускорения.
2. Параболическая (полином 2-ой степени) форма тренда:
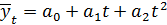
Для данного типа кривой постоянными являются вторые разности (ускорение), а нулевыми – третьи разности.
Параболическая форма тренда соответствует ускоренному или замедленному изменению уровней ряда с постоянным ускорением.
Если 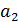 < 0 и
< 0 и 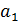 > 0, то квадратическая парабола имеет максимум, если
> 0, то квадратическая парабола имеет максимум, если 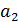 > 0 и
> 0 и 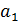 < 0 – минимум.
< 0 – минимум.
3. Логарифмическая форма тренда:
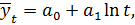
где 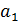 – константа тренда.
– константа тренда.
Логарифмическим трендом может быть описана тенденция, проявляющаяся в замедлении роста уровней ряда динамики при отсутствии предельно возможного значения. При достаточно большом t логарифмическая кривая становится мало отличимой от прямой линии.
4. Мультипликативная (степенная) форма тренда:
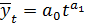
5. Полином 3-ей степени:
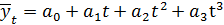
В рамках данной работы необходимо построить линейную модель тренда, полиномы 2-й и 3-й степени и степенную модель.
Для решения поставленной задачи по аналитическому сглаживанию динамических рядов в системе STATISTICA нам потребуется создать дополнительную переменную.
Нам предстоит построить уравнение тренда, которое по существу является уравнением регрессии, в котором в качестве фактора выступает «время». Создаем переменную «t», содержащую интервалы времени.
Первый период включает в себя 16 лет, с 1977-1992 гг., значит переменная «t» ,будет состоять из натуральных чисел от 1 до 16, соответствующих годам.
Второй период включает в себя 9 лет, с 1993-2001 гг., значит переменная «t» ,будет состоять из натуральных чисел от 1 до 9.
Третий период включает в себя 7 лет, с 2002-2008 гг., значит переменная «t» ,будет состоять из натуральных чисел от 1 до 7.
|
из
5.00
|
Обсуждение в статье: Аналитическое выравнивание динамического ряда. Построение модели тренда |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

