Проверка значимости коэффициентов связи

Следующей задачей корреляционного анализа является проверка значимости характеристик связи (коэффициентов корреляции, частных коэффициентов корреляции и коэффициентов детерминации) на уровне значимости , которая может быть осуществлена двумя способами. Первый способ основан на сравнении наблюдаемого значения статистики с критическим значением, при этом если (для коэффициентов корреляции и частных коэффициентов корреляции), (для коэффициентов детерминации), тос вероятность ошибки 0,05 нулевая гипотеза о незначимости соответствующих характеристик связи отклоняется. Второй способ предполагает сравнение значения вероятности принятия нулевой гипотезы о незначимости характеристики связи (наблюдаемого уровня значимости p) с заранее заданным уровнем значимости , при этом, если , то на 5%-ом уровне значимости нулевая гипотеза отклоняется и делается вывод о статистической значимости соответствующих характеристик связи.

Для проверки значимости коэффициента корреляции выдвигаются гипотезы:

(коэффициент корреляции незначим);

(коэффициент корреляции значим).

Для проверки гипотезы 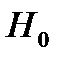используется статистика , которая при условии справедливости нулевой гипотезы распределена по закону Стьюдента с числом степеней свободы .

В Excel c помощью функции = СТЬЮДЕНТ.ОБР.2Х (0,05;78) получили:

Результаты проверки гипотез о незначимости коэффициентов корреляции представлены в Приложении И (Таблица И.1).

Аналогичным образом на основе информации, проверим значимость частных коэффициентов корреляции. При и числе степеней свободы 𝜗=n-k=80-5=75, критическая точка принимает следующее значение 1,992 Результаты проверки сведены в Приложении (Таблица И.2).

Для проверки значимости частного коэффициента корреляции выдвигаются гипотезы:

(частный коэффициент корреляции незначим);

(частный коэффициент корреляции значим).

Для проверки гипотезы 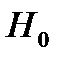используется статистика , которая при условии справедливости нулевой гипотезы распределена по закону Стьюдента с числом степеней свободы .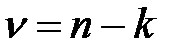

Проверим значимость коэффициентов детерминации.

Для проверки значимости коэффициента детерминации выдвигаются гипотезы:

(коэффициент детерминации незначим, т.е. признаки не оказывают значимого влияния на );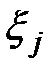

(коэффициент детерминации 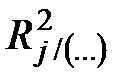значим, т.е. существует хотя бы один из признаков , оказывающих значимое влияние на ).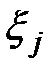

Для проверки гипотезы 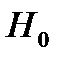используется статистика , которая при условии справедливости нулевой гипотезы распределена по закону Фишера-Снедекора с числом степеней свободы , .

Критическое значение определим с помощью функции F.ОБР.ПХ (Вероятность; Степени_свободы 1; Степени_свободы 2) табличного редактора Excel. Учитывая заданный уровень значимости и число степеней свободы , 80-5=45, критическая точка принимает следующее значение 2,494.

Результаты проверки представлены в Таблице И.3 (Приложение И).