Дисперсия и среднее квадратическое отклонение. Коэффициент вариации

Дисперсия ()признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):

простая дисперсия для не сгруппированных данных:

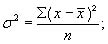(6.3)

взвешенная дисперсия для вариационного ряда:

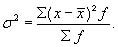(6.4)

Формула (6.4) применяется при наличии у вариантов своих весов (или частот вариационного ряда).

Формулу для расчета дисперсии (6.3) можно преобразовать, учитывая, что :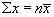

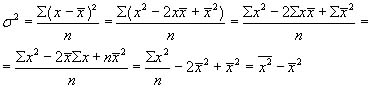
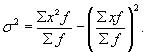(6.5)

Таким образом, дисперсия равна разности средней из квадратов вариантов и квадрата их средней.

Техника вычисления дисперсии по формулам (6.3), (6.4) достаточно сложна, а при больших значениях вариантов и частот может быть громоздкой. Расчет можно упростить, используя свойства дисперсии (доказываемые в математической статистике).

Приведем два из них:

первое _ если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не изменится;

второе _ если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответственно уменьшится или увеличится в i2 раз.

Используя второе свойство дисперсии, разделив все варианты на величину интервала, получим следующую формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:

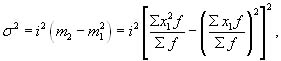(6.6)

где _ дисперсия, исчисленная по способу моментов;

i _ величина интервала;

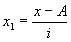_ новые (преобразованные) значения вариантов (А _ условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой);

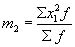_ момент второго порядка;

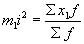_ квадрат момента первого порядка.

Расчет дисперсии по формуле (6.6) менее трудоемок.

Среднее квадратическое отклонение () равно корню квадратному из дисперсии:

а) для несгруппированных данных

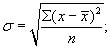(6.7)

б)для вариационного ряда

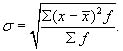(6.8)

Среднее квадратическое отклонение () _ это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения.

В статистической практике часто возникает необходимость сравнения вариаций различных признаков, например, вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. Для подобных сопоставлений показатели абсолютной колеблемо сти признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией заработной платы, выраженной в рублях.

Для осуществления такого рода сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют относительный показатель вариации _ коэффициент вариации.

Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

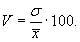(6.9)

Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %.