Сила давления жидкости на плоскую стенку

Сила давления жидкости на плоскую стенку равна произведению гидростатического давления р_с в центре тяжести площади стенки на площадь стенки S, т.е.

(2.6)

Центр давления(точка приложения силы F)расположен ниже центра тяжести площади или совпадает с последним в случае горизонтальной стенки.

Расстояние между центром тяжести площади и центром давления в направлении нормали к линии пересечения плоскости стенки со свободной поверхностью жидкости равно

(2.7)

где J₀ – момент инерции площади стенки относительно оси, проходящей через центр тяжести площади и параллельной линии пересечения плоскости стенки со свободной поверхностью;

у_с – координата центра тяжести площади.

Сила давления жидкости на криволинейную стенку, симметричную относительно вертикальной плоскости, складывается из горизонтальной F_Г и вертикальной F_В составляющих:

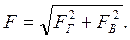(2.8)

Горизонтальная составляющая 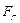равна силе давления жидкости на вертикальную проекцию данной стенки:

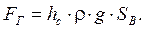(2.9)

Вертикальная составляющая 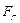равна весу жидкости объеме V, заключенном между данной стенкой, свободной поверхностью жидкости и вертикальной проецирующей поверхностью, проведенной по контуру стенки. Если избыточное давление р₀ на свободной поверхности жидкости отлично от нуля, то при расчете следует эту поверхность мысленно поднять (или опустить) на высоту (пьезометрическую высоту) .

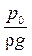Относительный покой жидкости - это равновесие ее в движущихся сосудах, когда помимо силы тяжести на жидкость действует вторая массовая сила - сила инерции переносного движения, причем эта сила постоянна по времени.

Возможны два случая относительного покоя жидкости: в сосуде, движущемся прямолинейно и равноускоренно, и в сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью. В обоих случаях поверхности уровня, т.е. поверхности равного давления, и в том числе свободная поверхность жидкости, принимают такой вид, при котором равнодействующая массовая сила нормальна к этим поверхностям во всех их точках.

В сосуде, движущемся прямолинейно и равноускоренно, поверхности уровня будут плоскими.

В сосуде, равномерно вращающемся вокруг вертикальной оси, поверхности уровня представляют собой параболоиды вращения, ось которых совпадает с осью вращения сосуда.

Уравнение поверхности уровня (в частности, поверхности жидкости в открытом сосуде) в цилиндрических координатах (r, z) имеет вид

(2.10)

где z₀ – вертикальная координата вершины параболоида поверхности уровня;

r, z – координаты любой точки поверхности уровня.

Закон распределения давления по объему жидкости, вращающейся вместе с сосудом, выражается уравнением

(2.11)

где р₀ – давление в точке с координатами r = 0, z = z₀.

Таким образом, повышение давления в жидкости, возникающее вследствие ее вращения, равно

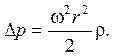(2.12)

Примеры решения задач

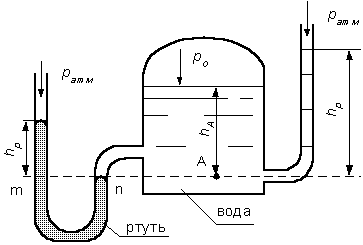Рис.2.8.

Пример 1. Определить абсолютное и избыточное гидростатическое давление
в точке А (рис. 2.8), расположенной в воде на глубине , и пьезометрическую высоту для точки А, если абсолютное гидростатическое давление на поверхности .

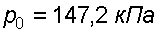Решение:

Согласно основного уравнения гидростатики абсолютное гидростатическое давление в точке А определится:

.

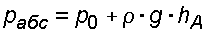Избыточное давление в точке А равно:

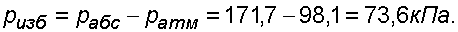
Пьезометрическая высота для точки А равна:

Можно отметить, что пьезометром удобно измерять только относительно малые давления, в противном случае требуется большая высота пьезометра, что неудобно в эксплуатации.

Определить эти же величины U – образным манометром, заполненным ртутью. По поверхности раздела ртути и воды давления со стороны резервуара и открытого конца манометра будут одинаковы:

Следовательно, избыточное давление в точке А уравновешивается весом столба ртути высотой 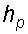над поверхностью раздела :

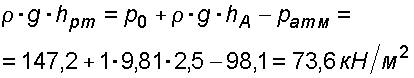
Находим высоту ртутного столба :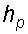

,

где 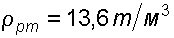– плотность ртути.

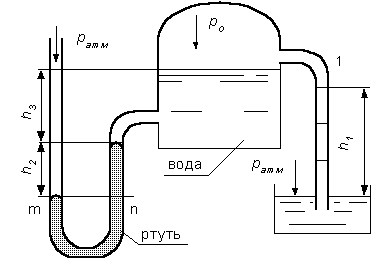Рис.2.9.

Пример 2. Определить давление в резервуаре 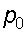(рис. 2.9) и высоту подъема уровня в трубке 1, если показания ртутного манометра .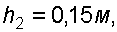

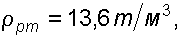
Решение:

Запишем условия равновесия для ртутного манометра для плоскости

а) со стороны резервуара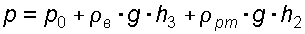

б) со стороны манометра ,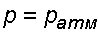

тогда

Таким образом, в резервуаре – вакуум, величина которого равна:

Условия равновесия трубки 1

 

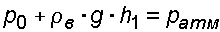
Пример 3.

Рис.2.10.

Определить манометрическое давление в трубопроводе А (рис. 2.10),

если высота столба ртути по пьезометру 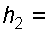25 см. Центр трубопровода расположен на 40 см ниже линии раздела между водой и ртутью.

Решение: Находим давление в точке В. Точка В расположена выше точки А на величину , следовательно, давление в точке В будет равно

.

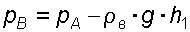В точке С давление будет такое же, как в точке В, то есть

.

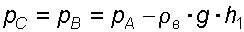Определим давление в точке C, подходя, справа

.

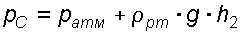Приравнивая оба уравнения, получаем

.

Отсюда манометрическое давление

.

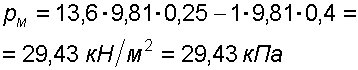
Пример 4.

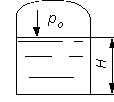Рис.2.11.

Определить все виды гидростатического давления в баке с нефтью на глубине (рис. 2.11), если давление на свободной поверхности нефти . Плотность нефти .

Решение: 1. Абсолютное гидростатическое давление у дна

2. Избыточное (манометрическое) давление у дна

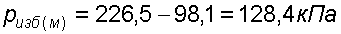
3. Избыточное давление создаваемое столбом жидкости

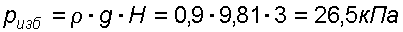
4. Избыточное давление на свободной поверхности

Пример 5. Определить избыточное давление воды в трубе по показаниям батарейного ртутного манометра (рис. 2.12).

Рис.2.12.

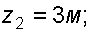
Отметки уровней ртути от оси трубы: Плотность ртути , плотность
воды .

Решение: Батарейный ртутный манометр состоит из двух последовательно соединенных ртутных манометров. Давление воды в трубе уравновешивается перепадами уровней ртути, а так же перепадами уровней воды в трубках манометра. Суммируя, показания манометра от открытого конца до присоединения его к трубе получим: