Определители второго и третьего порядков

Определитель квадратной матрицы второго порядка задается формулой:

. (5.1)

Определитель матрицы третьего порядка вычисляется по формуле:

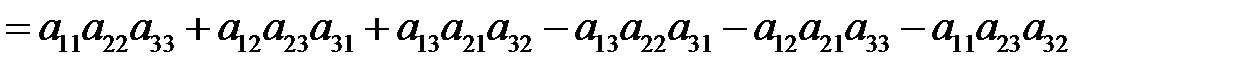. (5.2)

Чтобы запомнить эту формулу, построим вспомогательную матрицу размера , полученную из матрицы добавлением к ней справа первого и второго столбцов. В этой матрице соединим сплошными линиями элементы, стоящие на главной диагонали матрицы и на параллельных ей отрезках, а элементы, стоящие на побочной диагонали и параллельных ей отрезках – пунктирными (см. рис.).

Произведения матричных элементов, соединенных сплошной линией, входят в определитель матрицы со знаком плюс, а пунктирной – со знаком минус.

Основные свойства определителя

1. , где – матрица, транспонированная к матрице, т.е. матрица, строки которой являются столбцами матрицы с теми же номерами.

Из этого равенства следует, что любое утверждение, верное для столбцов определителя, верно и для строк определителя и обратно.

2. При умножении произвольной строки определителя на число, определитель умножается на это число.

3. Если строка определителя представлена в виде суммы двух строк, то определитель равен сумме двух определителей, у каждого из которых на месте данной строки стоит одно из слагаемых, а остальные строки прежние.

4. При перестановке двух строк определитель меняет знак.

5. Определитель равен нулю тогда и только тогда, когда его строки линейно зависимы.

6. Определитель не изменится, если к строке прибавить линейную комбинацию других строк определителя.

Указанные свойства выполняются для определителей любого порядка.

Методы вычисления определителей

Метод разложения определителя по столбцу. Пусть – определитель матрицы, полученной из матрицы вычеркиванием строки c номером и столбца с номером . Алгебраическим дополнением элемента квадратной матрицы называется число . Формула разложения определителя любого порядка по элементам столбца имеет следующий вид:

. (5.3)

Формула для разложения определителя по элементам строки имеет вид

. (5.4)

Применение этого метода наиболее эффективно, если сначала, с помощью линейных преобразований строк матрицы, не меняющих определителя (см. свойство 6), обратить в ноль почти все элементы некоторого столбца, а затем применить формулу разложения по этому столбцу. Вычисление определителя значительно облегчается, если с помощью указанных выше преобразований удается привести матрицу к треугольному или блочно треугольному виду.

Примеры решения типовых задач