Е.1.5.2.5 Коэффициент формы колебаний

(1) Коэффициент формы колебаний К определен по формуле

, (Е.9)

где m — определяется по Е.1.5.2.4(1);

F_i,y(s) — i-ая форма поперечных колебаний (см. F.3);

l_j — длина конструкции между двумя узловыми точками (см. рисунок Е.3).

(2) Для некоторых простых конструкций, колеблющихся в основной форме колебаний, коэффициент указан в таблице Е.5.

Е.1.5.2.6 Количество циклов загружений

(1) Количество N циклов загружений, вызываемых вихревым возбуждением колебаний, можно определять по формуле (Е.10).

, (Е.10)

где n_y — собственная частота, Гц, i-ой формы поперечных колебаний конструкции; приближенные методы указаны в приложении F;

v_crit — критическая скорость ветра, м/с, по Е.1.3.1;

v₀ — Ö2-кратное наиболее вероятное значения (модальная величина v_mod) распределения вероятностей Вейбулла средней скорости ветра, м/с;

Т — проектный срок службы в секундах, соответствующий 3,2 × 10⁷-кратному требуемому сроку службы в годах;

e₀ — коэффициент ширины диапазона частот, описывающий ширину диапазона скоростей ветра, индуцирующих вихревое возбуждение колебаний.

Примечание 1 — В национальном приложении можно устанавливать минимальное значение N. Рекомендуемое значение N ³ 10⁴.

Примечание 2 — Для значения v₀ может приниматься 20 % характеристической средней скорости ветра на высоте поперечного сечения, где возникает вихревое возбуждение (см. 4.3.1(1)).

Примечание 3 — Коэффициент ширины диапазона частот e₀ может принимать значения от 0,1 до 0,3.
Он может приниматься как e₀ = 0,3.

Е.1.5.2.7 Резонансное вихревое возбуждение для сгруппированных или расположенных в ряд
вертикальных цилиндров

(1) У сгруппированных или расположенных в ряд круговых цилиндров со связью и без нее (см. рисунок Е.4) могут возникать вызываемые вихревым возбуждением колебания.

Рисунок Е.4 — Сгруппированные или расположенные в ряд цилиндры

(2) Максимальное перемещение может оцениваться по формуле (Е.7) и с применением методов расчета по Е.1.5.2 и модификаций соответственно формулам (Е.11) и (Е.12).

Для цилиндров, расположенных в ряд, без связи применяют:

с_lat = 1,5с_lat(single) для ;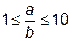

с_lat = с_lat(single) для ;

линейную интерполяцию для 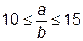; (Е.11)

для ;

St = 0,18 для ,

где с_lat(single) = с_lat по таблице Е.3.

Для цилиндров со связями применяют:

с_lat = K_ivс_lat(single) для 1,0 £ a/b £ 3,0,

где K_iv — коэффициент интерференции для вихревого возбуждения (таблица Е.8);

St — число Струхаля, по таблице Е.8;

Sc — число Скрутона, по таблице Е.8.

Для цилиндров со связями с a/b > 3,0 требуются специальные исследования.

Примечание 1 — Коэффициент 1,5с_lat для круговых цилиндров без связи является грубым приближением. Это приближение рассматривается как консервативное.