 |
Главная |
Методы и модели анализа динамики и прогнозирования лог.процессов
|
из
5.00
|
Динамика процессов в логистике анализируется при помощи статистических методов, а прогнозирование осуществляется на основе теории вероятностей. Они тесно взаимосвязаны между собой: например, на основе статистических данных строятся кривые распределения вероятностей. Т.е. для того чтобы делать прогнозы, мы должны оценить существующую ситуацию, динамику её развития и на основе этой информации предполагать характер развития системы в будущем. Методы мат. статистики также позволяют выявить характер связи между различными явлениями, установить причины и следствия.
В логистике часто применяется корреляционно-регрессионный анализ, с помощью которого выявляются качественные и количественные влияния различных факторов на показатели логистической деятельности. Этот анализ позволяет измерять тесноту связи между величинами и строить теоретические зависимости влияния одной величины на другую, т. е. уравнения регрессии. Для оценки динамики выявляется зависимость между полученными статистическими данными, потому что нужно понять: закономерны эти данные (верные данные – залог правильного прогноза) или являются случайными величинами (и тогда на них не следует опираться при прогнозировании).
В качестве примера можно сказать, что в логистике часто анализируются следующие величины:
1). х – товарный запас (тыс. руб.),
у – объем продаж (тыс. руб./день.).
2). х – надежность снабжения (поставок),
у – величина производственного запаса.
3). х – доля поставок точно в срок (% от объема поставок),
у – величина производственного запаса (млн руб.).
Теснота связи измеряется коэффициентом r. Примеры различной тесноты связи (рис):
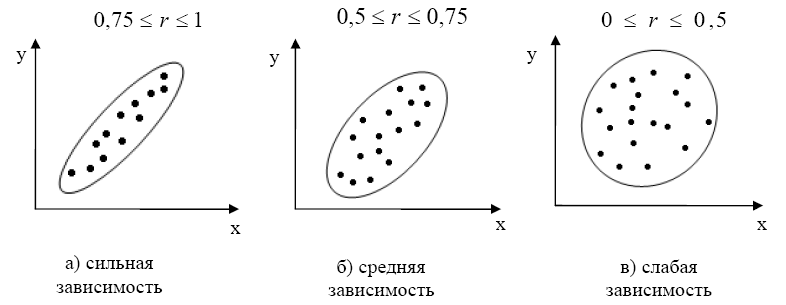
Так же динамика процессов оценивается путём сравнения данных за базовый период и отчётный для определения темпов роста.
Получив и проанализировав статистические данные, можно приступать к прогнозированию. Прогнозирование возможно осуществлять путём экстраполяции полученного на предыдущем этапе тренда на несколько периодов вперёд. Тренд в данном случае – не что иное, как уравнение регрессии (уравнение, связывающее исследуемые величины). А возможно и применение методов теории вероятностей.
Случайные отклонения сопутствуют любому закономерному процессу, а тем более логистическим процессам в рыночной экономике. Теория вероятностей в логистике рассматривает случайные величины, обусловленные логистическими процессами и операциями.
Случайные (стохастические) величины в логистике:
1) Спрос (платежеспособность).
2) Объем реализации (объем продаж).
3) Длительность (период реализации).
4) Выручка от реализации продукции.
5) Издержки:
a) - общие;
b) - логистические;
c) - транзакционные.
6) Время погрузки-выгрузки транспортных средств.
7) Время доставки (перемещения продукции).
8) Уровень использования грузоподъемности и грузовместимости транспортных средств.
9) Время обслуживания покупателей (потребителей).
10) Товарооборот торгового предприятия.
11) Оборот оптово-торговой базы.
12) Поток потребителей (поток заявок на обслуживание).
13) Время занятости средств обслуживания.
14) Движение товарного запаса.
15) Объем партии отгрузки реализуемой продукции.
16) Распределение продукции по группам АВС.
17) Процесс поставки – надежность поставок и другие.
Если изучаемое явление представляется в виде полной группы событий, которые несовместимы и равновозможны, то вероятность (p) данного события равна отношению числа (m) благоприятствующих этому событию случаев к общему числу (n) возможных случаев, т. е. вероятность равна:
р=m/n
На практике рассматривается статистическая вероятность, в результате накопленных статистических данных о благоприятствующих событиях m и общего числа событий n.
График распределения вероятностей может иметь разный вид, в зависимости от того, по какому закону распределены вероятности.
1). Распределение по нормальному закону.


2). Экспоненциальное распределение.


3). Биномиальное распределение.

4). Распределение Пуассона.
Вероятность того, что в течение времени t произойдет ровно m событий, определяется по формуле:
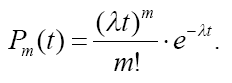
|
из
5.00
|
Обсуждение в статье: Методы и модели анализа динамики и прогнозирования лог.процессов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

