Аналитическая интерпретация

Постановка задачи:

Индивид А. .

Индивид В. .

Балансовые уравнения:

.

Где: – запас первого товара у потребителя А, – запас второго товара у потребителя А, – запас первого товара у потребителя В, – запас второго товара у потребителя В, = + – совокупный запас первого блага в экономике, = + – совокупный запас второго блага в экономике, = – – чистый избыточный спрос потребителя А на первый товар, = – – чистый избыточный спрос потребителя А на второй товар, = – – чистый избыточный спрос потребителя В на первый товар, = – – чистый избыточный спрос потребителя В на второй товар, = + = – – совокупный избыточный спрос на первый товар, = + = – – совокупный избыточный спрос на второй товар.

Определение.Общее экономическое равновесие – это такое состояние экономической системы, когда на каждом из рассматриваемых рынков спрос равен предложению или, другими словами, избыточный рыночный спрос равен нулю. Т.е. традиционно общее экономическое равновесие трактуется как такое состояние экономической системы, в котором существует вектор цен, единый для всех хозяйствующих субъектов, при котором:

При – благо находится в свободном доступе.

Но вернемся к нашей задаче. Шести неизвестным соответствует шесть уравнений: два уравнения, относящиеся к эквимаржинальному принципу ( ), два уравнения бюджетных ограничений, два балансовых уравнения. Но в действительности независимых уравнений на одно меньше, чем количество неизвестных, т.к. при сложении двух бюджетных уравнений и замене переменных с использованием одного из балансовых уравнений мы получаем другое балансовое уравнение. Следовательно, решение задачи возможно при уменьшении ее размерности. Принимая цену одного из благ за единицу, определяем вектор относительных (реальных) равновесных цен. Для установления уровня цен и вектора денежных (номинальных) цен используется уравнение количественной теории денег. Но Дон Патинкин[23] обратил внимание на то, что теория ценности, определяющая пропорции обмена товаров, т.е. их относительные равновесные цены, не согласуется с количественной теорией денег, служащей для определения номинальных цен. Так, например, при удвоении уровня цен равновесие сохраняется на всех рынках, за исключением рынка денег. Для устранения этого противоречия Д. Патинкин включил в число аргументов функции полезности индивида реальные кассовые остатки. В этом случае объем избыточного спроса на рынках благ и денег тоже зависит от реальных кассовых остатков, и неправильной дихотомии не возникает.

Впервые в экономической теории Л. Вальрас[24] дал подробное описание статического равновесия на основе своей модели (1889, 1896, 1900). При этом, как замечает М. Блауг[25], равновесие выстраивалось шаг за шагом в процессе постепенного убывания абстракции, начиная со случая двух сторон и бартерного обмена двумя товарами и заканчивая многосторонним обменом многими товарами при данных запасах благ, производством и рынками производственных услуг, сбережением и формированием капитала и, наконец, использованием денег и кредита. А во второй половине ХХ века К. Эрроу совместно с Дж. Дебре[26] и независимо от них Л. МакКензи[27] строго доказали существование общего статического равновесия для своих моделей совершенно конкурентной экономики.

Определение.В равновесной экономике действует закон Вальраса, утверждающий, что стоимость совокупного (агрегированного) чистого спроса тождественно равна нулю: .

Для нашей экономики обмена (2х2) тождество принимает вид: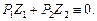

Доказательство.Вусловиях оптимума для каждого i-го индивида бюджетное ограничение выполняется в виде равенства. Например, в нашем случае для индивида А оно может быть записано в следующем виде:

Сумма таких равенств для всех индивидов дает нулевую величину агрегированного чистого спроса в стоимостном выражении:

Что и утверждает закон Вальраса.

Из закона Вальраса вытекают два важных следствия.

Если в экономике, состоящей из n рынков при некотором векторе цен , избыточный спрос равен нулю на (n–1) рынках, то он оказывается нулевым и на оставшемся n-м рынке.

Величины избыточного спроса в экономике не могут быть одновременно одного знака.

 

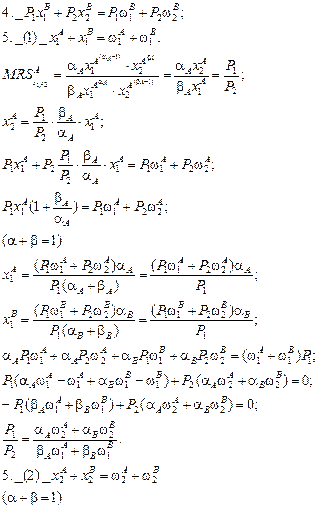
Рассмотрим теорему о существовании общего экономического равновесия.

Определение.Поскольку функция спроса каждого из потребителей на каждый из товаров является непрерывной по ценам при любом первоначальном распределении благ между потребителями (одно из допущений[28]), будет существовать равновесный вектор цен, соответствующий определению общего равновесия: – для экономических благ; – для блага, находящегося в свободном доступе.

Рис. 5

 

По следствию из закона Вальраса при отсутствии равновесия (на каждом рынке) экономическая система может находиться в некотором состоянии А во втором квадранте или в некотором состоянии В четвертом квадранте (см. рис. 6). Все состояния, соответствующие первому и третьему квадрантам имеют один и тот же знак избыточного спроса обоих товаров ( ), и поэтому нами не рассматриваются.

Рис. 6

 

По теореме о нуле непрерывной функции (первая теорема Больцано–Коши), если непрерывная функция принимает на концах отрезка положительное и отрицательное значения (значения разные по знаку), то существует на рассматриваемом отрезке точка, в которой она принимает нулевое значение.

Пусть ([a,в]) такое, что f(c)=0

Т.е. при переходе из точки А в точку В величина избыточного спроса по каждому из товаров примет нулевое значение в силу того, что совокупный избыточный спрос является непрерывной функцией от цен. Так, если в точке , то по следствию из закона Вальраса . В точке величины избыточного спроса при положительных ценах одновременно равны нулю, т.е. достигается общее экономическое равновесие.

 

В точке также наблюдается равновесие, но если первое благо является экономическим ( ), то второе благо находится в свободном доступе ( ). Аналогично, точка отражает равновесие системы при условии, что первое благо находится в свободном доступе .

Обобщая, стоит отметить, что все теоремы существования равновесия сводятся к применению теорем о неподвижных точках для некоторого искусственно построенного отображения. В зависимости от свойств этого отображения применяют, например, «теорему Брауэра (которая работает для непрерывных функциональных отображений) или теорему Какутани (которая работает для полунепрерывных, в том числе и многозначных, отображений). Еще один способ доказательства существования равновесия основан на сведении равновесия по Вальрасу к равновесию по Нэшу в соответствующим образом построенной игре и использовании теоремы о существовании равновесия по Нэшу, доказательство которой, в свою очередь, также базируется на теореме Какутани»[29].

Отдельно следует рассмотреть вопросы единственности и стабильности равновесия. Единственность равновесия в рассматриваемой модели вытекает из используемых предпосылок: поведенческие функции производителей и потребителей непрерывны, монотонны и выпуклы.

С другой стороны, «экономическая система считается глобально стабильной, если для любого первоначального вектора цен P(0) и равновесного вектора цен выполняется равенство: .

Как мы видели в моделях общего равновесия, достижение равновесия – это процесс «нащупывания» верной цены. При одних ценах может наблюдаться избыточный спрос, при других – избыточное предложение. Избыточный спрос толкает цены вверх, избыточное предложение сопровождается падением цен»[30]. Для иллюстрации этого положения рассмотрим модель межрыночных взаимоотношений (рассматривается взаимодействие рынков двух благ – X и Y). В качестве отравной точки возьмем случай симметричных однонаправленных взаимодействий. В функциях избыточного спроса каждого из благ в качестве аргументов присутствуют цены на данное и сопряженное благо , , а также величина первоначального запаса блага . Для общих субститутов, для которых характерен такой тип межрыночного взаимодействия, коэффициенты перекрестной ценовой эластичности положительны. Тогда (если ограничимся линейными зависимостями):

,

,

В условиях частичного равновесия:

следовательно, кривая избыточного спроса (в системе координат , – восходящая прямая линия. Аналогично можно получить выражение для кривой частичного равновесия .

Так как величины прямых эффектов всегда превосходят по модулю прямые эффекты, то прямые и всегда имеют углы наклона к осям их цен превышающие , а следовательно, всегда имеют только одну точку пересечения.

На рисунке 7 определены направления изменения цен и динамика избыточного спроса в случаях отклонения цен от равновесного уровня. Рыночный механизм приводит к такому приспособлению цен, при котором устанавливается единственное устойчивое равновесие.

Рис. 7

 

Аналогично, можно показать, что единственная точка устойчивого равновесия достигается при симметрично разнонаправленном взаимодействии и при асимметричном. Так, в случае общих комплементов значения коэффициентов перекрестной ценовой эластичности отрицательны. Тогда:

,

,

В условиях частичного равновесия:

Следовательно, кривая частичного равновесия – нисходящая прямая линия. Рыночный механизм обеспечивает установление общего равновесия в случае двух нисходящих линий и в случае сочетания нисходящей и восходящей линий. Никаких принципиальных отличий от вышерассмотренной схемы симметрично однонаправленного взаимодействия относительно изменения цен при альтернативных типах взаимодействия нет.

 

Общее экономическое равновесие и оптимальность
по Парето. Диаграмма Эджуорта:
двухсубъектная двухпродуктовая экономика

 

Материал для следующих разделов предоставлен проф. Вереникиным А.О. Сбалансированность экономической системы: Микро- и макроаспекты. М.: ТЕИС. 2010. сс. 198–201).

На диаграмме Эджуорта объединяются графики (см. рис. 8), иллюстрирующие оптимальный выбор каждого из двух потребителей.

Рис. 8

 

Если наборы , эффективны по Парето, то в данной точке диаграммы Эджуорта линии безразличия двух потребителей касаются, то есть соответствующие предельные нормы замещения в точке касания равны. В условиях общего экономического равновесия их общей касательной является бюджетное ограничение каждого из потребителей с угловым коэффициентом, равным отношению цен :

.

Итак, для эффективных по Парето, находящихся на контрактной кривой наборов , справедливо равенство:

.

Рис. 9.Диаграмма Эджуорта

 

Различные точки на кривой контрактов соответствуют всевозможным вариантам распределения доходов между потребителями.

Одним из вариантов меры неравенства распределения доходов в обществе является коэффициент Джини. Его расчет можно проиллюстрировать графически с помощью кривой Лоренца (см. рис. 10). Кривая Лоренца отражает зависимость между накопленной процентной долей населения (от нуля до ста процентов) и соответствующей долей совокупных доходов, получаемой этими людьми (также в процентах – от нуля до ста). В случае абсолютного равенства линия Лоренца вырождается в прямую линию. Кривая Лоренца выпукла вниз, причем чем больше ее выпуклость, тем выше неравенство в распределении доходов в обществе.

Рис. 10

 

Коэффициент Джини G рассчитывается как отношение площади над кривой Лоренца, ограниченной сверху диагональю АС квадрата AECB, то есть линией равномерного распределения, к площади треугольника ACB: . При абсолютном равенстве коэффициент Джини равен нулю, а при абсолютном неравенстве G=1.

Кривая контрактов и кривая производственных
возможностей. Равновесие в производстве
и потреблении

В модели экономики производства аналогичное соотношение, задающее уравнение линии производственных контрактов, возникает из решения задач максимизации прибыли для каждого из производителей:

значит,

значит, .

В итоге получаем соотношение, задающее характеристики общего равновесия и народнохозяйственной оптимальности по Парето применительно к производственной экономической системе: .

Моделирование сбалансированности хозяйственной деятельности предприятий в экономической системе в целом позволяет охарактеризовать производственные возможности общества (рис. 11). Изменение структуры выпуска продукции вдоль границы производственных возможностей общества подразумевает перераспределение факторов хозяйственной деятельности из одних отраслей в другие. При этом трудовые и материальные ресурсы в рамках экономической системы в целом используются полностью, и их величина в каждый данный момент фиксирована: , , то есть их дифференциалы тождественно равны нулю: , 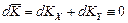; откуда следует, что , .

А значит, в условиях совершенной конкуренции, при сложившихся ценах на факторы производства неизменными остаются и совокупные его издержки: их увеличение в одних отраслях означает снижение на ту же величину в других:

.

Таким образом, альтернативные издержки производства блага X в единицах блага Y могут быть рассчитаны как отношение соответствующих предельных издержек:

.

Итак, предельная норма трансформации – это, с одной стороны, количество одного блага, от производства которого необходимо отказаться при увеличении производства другого на единицу; а с другой – это отношение предельных издержек производства каждого блага. Но, поскольку в условиях совершенной конкуренции предельные издержки равны цене выпускаемой продукции, альтернативные издержки могут быть измерены через отношение цен:

.

Относительные цены в условиях общего экономического равновесия совпадают с относительными предельными издержками, которые, в свою очередь, равны предельной норме трансформации, или альтернативным издержкам. Таким образом, в масштабах хозяйственной системы общества в целом на основе соотношения предельных альтернативных издержек производства благ определяется структура стоимостных пропорций между отраслями и секторами экономики.

Предельную норму трансформации можно задать еще одним способом: как отношение предельного продукта ресурса в производстве одного блага к предельному продукту фактора при производстве другого блага. Другими словами, можно показать, что из модели общего экономического равновесия следует равенство альтернативных издержек обратной величине относительной предельной производительности каждого из ресурсов. В качестве составных частей модели общего экономического равновесия выступают задачи оптимизации производства для каждого из производителей, работающих в народном хозяйстве страны. Поскольку множитель Лагранжа λ в задаче условной минимизации издержек, входящей составной частью в задачу максимизации прибыли, представляет собой предельные издержки производства, используя условия минимизации издержек, можно записать:

Аналогичное соотношение выполняется для производителя продукта Y:

Выше было показано, что:

Поэтому с учетом полученных нами выражений для предельных издержек предельную норму трансформации можно следующим образом выразить через цены и предельные продукты факторов производства:

Рис. 11

Теория квазиоптимума

Возникновение монополии даже на одном рынке нарушает Парето-эффективное распределение ресурсов во всей экономике:

; P_X^M>P_X^C.

В результате искажаются:

- цены на всех рынках, а не только на монополизированном;

- объемы производства, по сравнению с эффективными объемами производства на конкурентных рынках;

- распределение ресурсов на всех рынках, поскольку неиспользуемые монополией ресурсы поглощаются другими отраслями.

Следствие. В случае, когда в одной отрасли или группе отраслей искажения не могут быть устранены, лучше отказаться от эффективности в другой отрасли (отраслях) с тем, чтобы сбалансировать экономику в целом.

Поскольку общее равновесие трудно достижимо, наиболее реальным является субоптимальное решение задачи оптимизации функционирования общественного производства (так называемая ситуация «second best»), достигаемое путем государственного регулирования экономики.

 

Пример № 1