 |
Главная |
Приложения двойного интеграла
|
из
5.00
|
Вычисление объема тела
Согласно геометрическому смыслу двойной интеграл 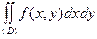
выражает объем цилиндрического бруса, ограниченного сверху поверхностью f(x,y), снизу – областью (D), лежащей в плоскости Oxy, с боков – цилиндрической поверхностью, образующие которой параллельны оси Oz, а направляющей является кривая, ограничивающая область (D).
Пример 8. Найти объем тела, ограниченного поверхностями  ,
,  .
.
Решение.
 Рис. 10
Рис. 10
| Данное тело представляет собой вертикальный цилиндр (рис. 10). Для построения тела заметим, что образующие параболического цилиндра  параллельны оси Oz, плоскость параллельны оси Oz, плоскость  параллельна плоскости xOz. Сверху тело ограничено частью плоскости параллельна плоскости xOz. Сверху тело ограничено частью плоскости  , поэтому f(x,y) = 4 – x – y. Основанием тела, т.е. областью интегрирования (D) является часть плоскости xOy, заключенная между параболой , поэтому f(x,y) = 4 – x – y. Основанием тела, т.е. областью интегрирования (D) является часть плоскости xOy, заключенная между параболой  и прямой и прямой  . Таким образом . Таким образом
 . .
|
Для вычисления двойного интеграла перейдем к повторному интегралу с внутренним интегрированием по переменной x и внешним – по переменной y. Для определения пределов интегрирования восстановим отдельно область
 Рис. 11
Рис. 11
| интегрирования (D) (рис. 11). Ордината точки пересечения параболы  с прямой с прямой  равна 1, следовательно, для области (D) равна 1, следовательно, для области (D)  , а переменная x изменяется от , а переменная x изменяется от  до до  . В итоге для искомого объема получается: . В итоге для искомого объема получается:

|
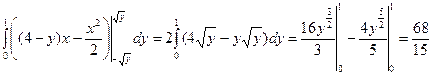 .
.
Ответ.  (куб. ед.)
(куб. ед.)
Пример 9. Найти объем тела, ограниченного поверхностями  .
.
Решение.
 Рис. 12
Рис. 12
| Данное тело представляет собой пересечение двух параболоидов вращения (рис. 12). Для построения тела найдем линию L пересечения данных поверхностей. Для этого решим систему:
 Исключая из этой системы z, получим
Исключая из этой системы z, получим 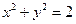 – уравнение вертикальной цилиндрической поверхности, которая проходит через линию L и проектирует ее на плоскость xOy. Полученное уравнение – уравнение вертикальной цилиндрической поверхности, которая проходит через линию L и проектирует ее на плоскость xOy. Полученное уравнение
|
будет и уравнением проекции линии L на плоскость xOy – окружности L1, ограничивающей область (D).
Объем искомого тела можно найти как разность объемов двух вертикальных цилиндрических тел, которые имеют общее нижнее основание (D) на плоскости xOy, а сверху ограничены данными поверхностями.

 .
.
Для упрощения вычисления интеграла преобразуем его к полярным координатам. Полагаем 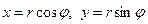 , тогда подынтегральная функция примет вид:
, тогда подынтегральная функция примет вид:
 .
.
Область интегрирования (D) ограничена окружностью 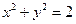 , уравнение которой в полярных координатах:
, уравнение которой в полярных координатах:  . Из рис.12 следует, что переменная r изменяется от 0 до
. Из рис.12 следует, что переменная r изменяется от 0 до  , а переменная φ от 0 до 2π.
, а переменная φ от 0 до 2π.
Используя формулу перехода к полярным координатам в двойном интеграле, получим:

 .
.
Ответ.  (куб. ед.)
(куб. ед.)
Вычисление площадей плоских фигур.
Двойной интеграл 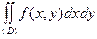 по квадрируемой области (D) в случае
по квадрируемой области (D) в случае  равен объему цилиндрического бруса с высотой 1, что численно совпадает с площадью S области (D), то есть
равен объему цилиндрического бруса с высотой 1, что численно совпадает с площадью S области (D), то есть
 .
.
Пример 10. Найти площадь плоской фигуры, ограниченной линиями  .
.
Решение.
 Рис. 13
Рис. 13
| Выполним построение данной фигуры (рис. 13). Первое уравнение  определяет нижнюю половину окружности определяет нижнюю половину окружности  с центром в точке (0,6) и радиусом равным 6. Второе уравнение с центром в точке (0,6) и радиусом равным 6. Второе уравнение  определяет верхнюю половину окружности определяет верхнюю половину окружности  с центром в точке (0,0) и радиусом равным 6. Используя третье уравнение x = 0 и условие с центром в точке (0,0) и радиусом равным 6. Используя третье уравнение x = 0 и условие  , устанавливаем, что необходимо рассматривать , устанавливаем, что необходимо рассматривать
|
область пересечения окружностей, расположенную в первой четверти. Площадь полученной фигуры будем находить по формуле:

Для вычисления двойного интеграла перейдем к повторному интегралу с внутренним интегрированием по переменной y и внешним – по переменной x. Для определения пределов интегрирования по переменной x найдем абсциссу точки пересечения окружностей.

Решив систему, получим координаты точки пересечения окружностей  . Таким образом, переменная x изменяется от 0 до
. Таким образом, переменная x изменяется от 0 до  . Для определения пределов внутреннего интеграла проведем через область (D) луч, параллельный оси Oy и сонаправленный с ней. Из чертежа следует, что точка входа луча в область (D) лежит на полуокружности, уравнение которой
. Для определения пределов внутреннего интеграла проведем через область (D) луч, параллельный оси Oy и сонаправленный с ней. Из чертежа следует, что точка входа луча в область (D) лежит на полуокружности, уравнение которой  , а точка выхода – на окружности
, а точка выхода – на окружности  . Эти уравнения являются нижним и верхним пределами внутреннего интеграла соответственно. В итоге получим:
. Эти уравнения являются нижним и верхним пределами внутреннего интеграла соответственно. В итоге получим:


Для вычисления  используем метод интегрирования по частям
используем метод интегрирования по частям



 .
.
Таким образом,  .
.
Разрешая это уравнение относительно  , получим:
, получим:
 .
.
Откуда 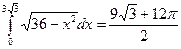 .
.
Возвращаемся к исходному интегралу:

 .
.
Ответ.  (кв. ед.)
(кв. ед.)
Пример 11. Найти площадь фигуры, ограниченной линиями  ,
,  .
.
Решение.
 Рис. 14
Рис. 14
| Приведем уравнения окружностей к каноническому виду (см. пример 7):  и и  . Радиусы окружностей равны 1 и 2, центры находятся в точках (0, 1) и (0, 2) (рис. 14). . Радиусы окружностей равны 1 и 2, центры находятся в точках (0, 1) и (0, 2) (рис. 14). 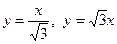 – уравнения прямых. Выполним построение данной фигуры (рис. 14).
Переходим к полярным координатам: – уравнения прямых. Выполним построение данной фигуры (рис. 14).
Переходим к полярным координатам:  , ,  .
Уравнения окружностей в полярной системе координат имеют вид: .
Уравнения окружностей в полярной системе координат имеют вид:
 и и  . .
|
Переведем в полярные координаты уравнения прямых:
 ,
,  ;
;
 ,
,  .
.
Таким образом переменная r изменяется от  до
до 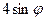 , а переменная φ от
, а переменная φ от  до
до 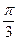 . Вычисляем площадь:
. Вычисляем площадь:

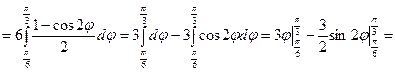
 .
.
Ответ.  (кв. ед.)
(кв. ед.)
|
из
5.00
|
Обсуждение в статье: Приложения двойного интеграла |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

