От пути интегрирования

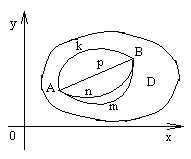Рис. 27

Пусть в замкнутой области (D) определены функции P(x,y) и Q(x,y), непрерывные в этой области вместе со своими частными производными и . Отметим в этой области любые две точки А и В и вычислим криволинейный интеграл 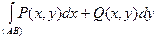(*)по различным кривым, идущим от А к В и лежащим

в области (D) (рис. 27). Получим различные значения интеграла (*). Если же окажется, что значение интеграла (*) по всем возможным кривым одно и то же, т.е.

,

то говорят, что криволинейный интеграл (*) не зависит в области (D) от пути интегрирования. Значение такого интеграла определяется заданием лишь начальной точки А и конечной точки В.

Выясним условия независимости криволинейного интеграла от пути интегрирования.

Рис. 28

Теорема 1.Для того, чтобы криволинейный интеграл 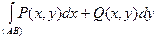в некоторой области (D) не зависел от пути интегрирования, необходимо и достаточно, чтобы он был равен нулю по любому замкнутому контуру, находящемуся в этой области.     Доказательство.

а) Необходимость. Пусть AlBkA – произвольный замкнутый контур в (D) (рис. 28). По условию

.

Тогда .

б) Достаточность. Пусть криволинейный интеграл по любому замкнутому контуру, например AlBkA, равен нулю. Тогда

.

Отсюда .

Замечание. Доказанная теорема имеет теоретическое значение, однако на практике мы не в силах вычислить интеграл по всем замкнутым контурам, хотя бы даже проходящим через заранее выбранные точки А и В.

Теорема 2.

Для того, чтобы интеграл 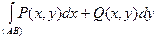не зависел от пути интегрирования в односвязной области (D), необходимо и достаточно, чтобы всюду в этой области .

Доказательство этой теоремы основано на использовании формулы Грина-Остроградского. Докажем, например, достаточность утверждения теоремы. Пусть в области (D) всюду выполняется равенство . Возьмем односвязную область (D) с границей . По формуле Грина-Остроградского

,

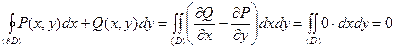а это означает, что интеграл не зависит от пути интегрирования.

Пример 19. Вычислить .

Решение.

Рис. 29

Здесь , , а также частные производные и - непрерывные функции в R2. Так как , то

данный интеграл не зависит от пути интегрирования. Для упрощения вычислений выберем путь, изображенный на рис. 29. Тогда, обозначая данный интеграл через I, получим:

Ответ. - 31.

Замечание. При интегрировании по горизонтальному пути учитываем, что y = 1, а dy = 0, а при интегрировании по вертикальному отрезку в подынтегральное выражение подставляем x = 2, dx = 0.

Если точку зафиксировать, а точку считать произвольной в области (D), то получаем функцию двух переменных

.

Если существует функция такая, что , то выражение называется полным дифференциалом.

Теорема 3.

Для того, чтобы выражение было полным дифференциалом некоторой функции, необходимо и достаточно, чтобы в области (D) выполнялось равенство .

Замечание. 1. Сравнивая теоремы 2 и 3, приходим к выводу: для того, чтобы криволинейный интеграл не зависел от пути интегрирования, необходимо и достаточно, чтобы выражение было полным дифференциалом некоторой функции.

2. Можно показать, что , где С – постоянная величина.

Пример 20. Проверить, является ли выражение

полным дифференциалом некоторой функции двух переменных Ф(x, y), и, если это так, найти Ф(x, y).

Решение.

Рис. 30

В данном выражении , . Частные производные , равны между собой и непрерывны. Следовательно данное выражение является полным дифференциалом некоторой функции.

Найдем эту функцию (рис. 30)

.

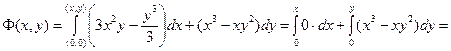
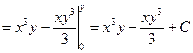Ответ. .

Замечание. Так как функция определяется с точностью до константы С, то в качестве точки можно выбрать любую точку из области непрерывности подынтегральной функции. Здесь для простоты вычислений взята точка .

Варианты контрольной работы №6.

1. Изменить порядок интегрирования.

1) ,

2) ,

3) ,

4) ,

5) ,

6) ,

7) ,

8) ,

9) ,

10) .

2. Вычислить:

1) ;

2) ;

3) ;

4) ;

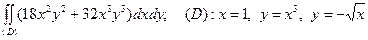5) ;

6) ;

7) ;

8) ;

9) ;

10) .