 |
Главная |
Линейная зависимость и линейная независимость системы векторов
|
из
5.00
|



Свойства линейной зависимости и линейной независимости векторов.
1.Если система векторов линейно независима, то и любая её часть также линейно независима
2. Если часть системы векторов линейно зависима, то и вся система линейно зависима
3. Система из двух векторов линейно зависима тогда и только тогда, когда эти векторы коллинеарны (Векторы и называются коллинеарными, если , где (один из них линейно выражается через другой)
38. Доказать, что любая совокупность n+1 векторов n-мерного пространства линейно зависимая
Любые n+1 элементы 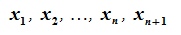 этого пространства линейно зависимы. Разложив эти элементы по базису, получим:
этого пространства линейно зависимы. Разложив эти элементы по базису, получим:
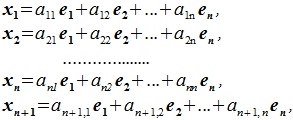
где a11, a12,..., an+1,n вещественные числа.
Пусть элементы 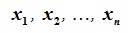 линейно независимы. Перепишем (3.4) в матричном виде:
линейно независимы. Перепишем (3.4) в матричном виде:
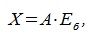
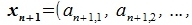 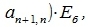
| (3.6) |
где 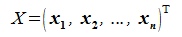 ,
, 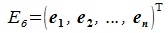 n×n-матрицы(элементы
n×n-матрицы(элементы 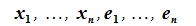 здесь являются вектор-строками),
здесь являются вектор-строками),

Так как 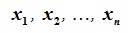 линейно независимы, матрица A имеет обратную матрицу A-1. Решив матричное уравнение (3.5) относительно
линейно независимы, матрица A имеет обратную матрицу A-1. Решив матричное уравнение (3.5) относительно  получим :
получим :
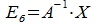
Подставляя (3.8) в (3.6), получим:
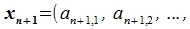 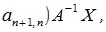
| (3.9) |
Как видно из уравнения (3.9) 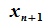 можно представить линейной комбинацией векторов .
можно представить линейной комбинацией векторов .
Следовательно векторы 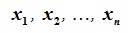
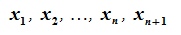 линейно зависимы. ■
линейно зависимы. ■
40. Понятие базиса n - мерного векторного пространства R(n). Разложение вектора по векторам базиса


43. Метод Жордана–Гаусса решения систем линейных уравнений
Система 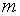 линейных уравнений с
линейных уравнений с 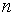 неизвестными
неизвестными  называется системой с базисом, если в каждом уравнении этой системы есть неизвестная, коэффициент при которой равен единице, а в остальных уравнениях коэффициенты при этой неизвестной равен нулю.
называется системой с базисом, если в каждом уравнении этой системы есть неизвестная, коэффициент при которой равен единице, а в остальных уравнениях коэффициенты при этой неизвестной равен нулю.
Примером системы линейных уравнений с базисом является система вида
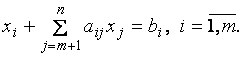
В этой системе неизвестные 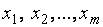 − базисные, а неизвестные
− базисные, а неизвестные 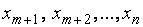 − свободные.
− свободные.
Рассмотрим систему 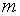 линейных уравнений с
линейных уравнений с 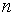 неизвестными, у которой выделены
неизвестными, у которой выделены 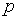 -й столбец и
-й столбец и 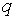 –я строка (
–я строка ( 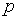 ,
, 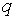 – фиксированные натуральные числа,
– фиксированные натуральные числа, 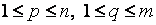 ):
):
 (3.1)
(3.1)
Пусть среди всех миноров 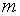 -го порядка, составленных из элементов основной матрицы системы (3.1), имеется хотя бы один отличный от нуля. Это требование обеспечит наличие у системы базиса, состоящего из
-го порядка, составленных из элементов основной матрицы системы (3.1), имеется хотя бы один отличный от нуля. Это требование обеспечит наличие у системы базиса, состоящего из 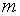 неизвестных
неизвестных 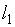 ,
, 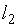 , …,
, …, 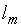 .
.
Рассмотрим алгоритмприведения системы (3.1) к системе с базисом:
1) по системе (3.1) заполним табл. 3.1;
2) в столбце 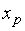 выберем отличное от нуля число и назовём его разрешающим элементом. Пусть
выберем отличное от нуля число и назовём его разрешающим элементом. Пусть  − разрешающий элемент;
− разрешающий элемент;
3) переходим к построению табл. 3.2, в которой вместо неизвестного базисного элемента 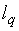 следует записать неизвестную
следует записать неизвестную 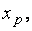 а все элементы
а все элементы 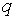 -й строки табл. 3.1 разделить на разрешающий элемент
-й строки табл. 3.1 разделить на разрешающий элемент 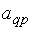 (при этом на месте разрешающего элемента в новой таблице появится 1). Вместо других элементов столбца
(при этом на месте разрешающего элемента в новой таблице появится 1). Вместо других элементов столбца 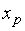 запишем нули, а числа оставшихся незаполненными ячеек пересчитаем по правилу прямоугольника, формулы которого имеют вид:
запишем нули, а числа оставшихся незаполненными ячеек пересчитаем по правилу прямоугольника, формулы которого имеют вид:


где 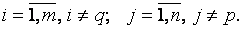
Таблица 3.1
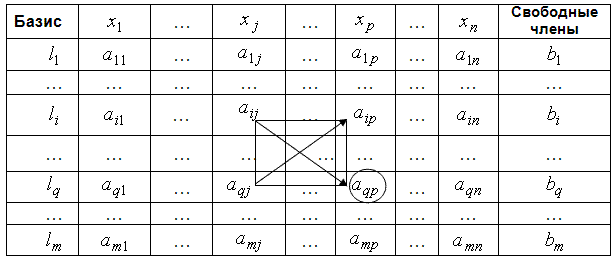
Правило прямоугольников схематично показано с помощью стрелок. Табл. 3.2 имеет вид:
Таблица 3.2
| Базис | 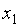
| … | 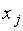
| … | 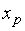
| … | 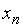
| Свободные члены |
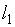
| 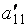
| … | 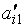
| … | … | 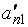
| 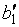
| |
| … | … | … | … | … | … | … | … | … |
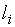
| 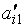
| … | 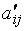
| … | … | 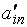
| 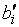
| |
| … | … | … | … | … | … | … | … | … |
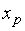
| 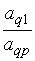
| … | 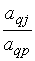
| … | … | 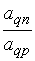
| 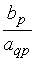
| |
| … | … | … | … | … | … | … | … | … |
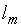
| 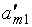
| … | 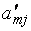
| … | … | 
| 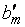
|
|
из
5.00
|
Обсуждение в статье: Линейная зависимость и линейная независимость системы векторов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

