 |
Главная |
Уравнения прямой на плоскости
|
из
5.00
|
Прямая – одна из простейших геометрических фигур. Алгебраическое уравнение прямой также имеет простой вид. Рассмотрим различные виды уравнений прямой на плоскости.
Уравнение прямой с угловым коэффициентом

| Уравнением прямой с угловым коэффициентом называется уравнение вида  , где , где 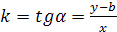 , точка , точка  лежит на прямой образующей с положительным направлением оси лежит на прямой образующей с положительным направлением оси 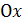 угол угол 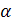 .
Если .
Если  , то , то  прямая проходит через начало координат.
Если прямая проходит через начало координат.
Если 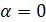 , то , то 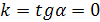 и и  прямая параллельна оси прямая параллельна оси 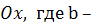 ордината точки пересечения прямой с осью ордината точки пересечения прямой с осью 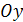 .
Если .
Если 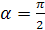 , то , то 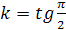 не существует и не существует и 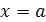  прямая параллельна оси прямая параллельна оси  , , 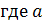 – абсцисса точки пересечения прямой с осью – абсцисса точки пересечения прямой с осью  .
Общее уравнение прямой
Общим уравнением прямой называется уравнение вида .
Общее уравнение прямой
Общим уравнением прямой называется уравнение вида
|
 ,
,
где 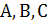 – произвольные числа, причем
– произвольные числа, причем  .
.
Частные случаи:
Если  и
и  , то общее уравнение прямой имеет неполный вид
, то общее уравнение прямой имеет неполный вид  и определяет прямую проходящую через начало координат
и определяет прямую проходящую через начало координат 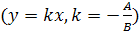 .
.
Если 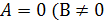 и
и  , то
, то  и определяет прямую параллельную оси
и определяет прямую параллельную оси  (
(  ,
, 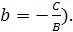
Если 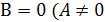 и
и  , то
, то 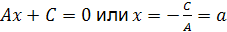 – прямая параллельная оси
– прямая параллельная оси 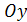 .
.
Если 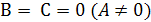 , то
, то 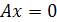
 прямая совпадает с осью
прямая совпадает с осью  .
.
Если 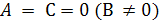 , то
, то 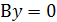
 прямая совпадает с осью
прямая совпадает с осью 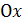 .
.
При  общее уравнение прямой
общее уравнение прямой 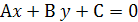 можно записать в виде:
можно записать в виде: 
Уравнение прямой в отрезках
Преобразуем общее уравнение прямой  следующим образом: перенесем
следующим образом: перенесем  в правую часть
в правую часть 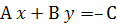 , разделим на
, разделим на 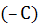 получим
получим  получаем уравнением прямой в отрезках которое имеет вид:
получаем уравнением прямой в отрезках которое имеет вид:
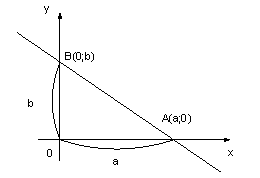
|
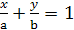 , где , где
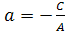 абсцисса точки пересечения прямой с осью абсцисса точки пересечения прямой с осью 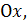
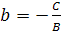 ордината точки пересечения с осью ордината точки пересечения с осью  .
Поэтому .
Поэтому 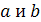 называют отрезками прямой на осях координат.
Формулу называют отрезками прямой на осях координат.
Формулу 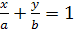 удобно использовать для построения прямой.
Для построения прямой достаточно взять две ее точки:
при удобно использовать для построения прямой.
Для построения прямой достаточно взять две ее точки:
при
|
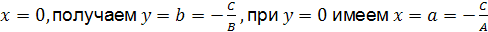
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Пусть прямая проходит через точку  перпендикулярно вектору
перпендикулярно вектору 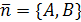 . Тогда вектор
. Тогда вектор  , где
, где  – произвольная точка прямой, перпендикулярен (или, еще говорят, ортогонален) вектору
– произвольная точка прямой, перпендикулярен (или, еще говорят, ортогонален) вектору 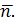
Поэтому координаты любой точки данной прямой удовлетворяют уравнению 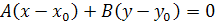 .
.
Определение. Вектор  называется нормалью к прямой или нормальным вектором.
называется нормалью к прямой или нормальным вектором.
Раскрыв скобки в уравнении 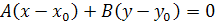 и приведя подобные получаем
и приведя подобные получаем 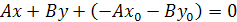 приняв
приняв 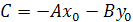 , получаем общее уравнение прямой
, получаем общее уравнение прямой  .
.
Уравнение прямой, проходящей через данную точку параллельно данному вектору (каноническое уравнение прямой)
Пусть прямая проходит через точку  параллельно вектору
параллельно вектору 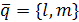 . Тогда вектор
. Тогда вектор  , где
, где  – произвольная точка прямой, коллинеарен вектору
– произвольная точка прямой, коллинеарен вектору  – направляющему вектору прямой
– направляющему вектору прямой 
 и координаты любой точки прямой
и координаты любой точки прямой  удовлетворяют каноническому уравнению прямой
удовлетворяют каноническому уравнению прямой
 .
.
Уравнением прямой, проходящей через данную точку в данном направлении
Уравнением прямой, проходящей через заданную точку 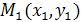 с заданным направлением называется уравнение вида
с заданным направлением называется уравнение вида 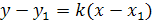 , где
, где  .
.
|
из
5.00
|
Обсуждение в статье: Уравнения прямой на плоскости |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

