 |
Главная |
Условия параллельности и перпендикулярности прямых
|
из
5.00
|
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов 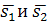 .
.
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны:
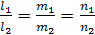 – условие параллельности прямых.
– условие параллельности прямых.
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:
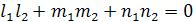 – условие перпендикулярности прямых.
– условие перпендикулярности прямых.
Пример. Найти уравнения прямой проходящей через точку  параллельно прямой
параллельно прямой  .
.
Решение. Поскольку искомая прямая параллельна данной прямой, то в качестве направляющего вектора искомой прямой можно взять направляющий вектор данной прямой.
По условию 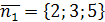 ,
, 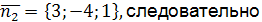
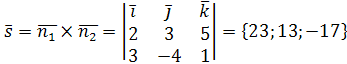 – отсюда уравнение искомой прямой имеет вид:
– отсюда уравнение искомой прямой имеет вид:  .
.

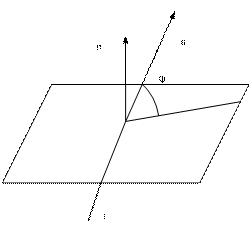
Угол между прямой, заданной каноническими уравнениями и плоскостью, определяемой общим уравнением
|
Определение. Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость.
Пусть прямая задана каноническими уравнениями 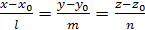 , а плоскость общим уравнением , а плоскость общим уравнением 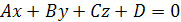 .
Рассмотрим векторы .
Рассмотрим векторы 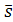 и и  .
Если угол между ними острый, то он будет .
Если угол между ними острый, то он будет
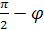 , а , а  .
Если угол между векторами .
Если угол между векторами 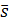 и и  тупой, то он равен тупой, то он равен 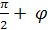 . .
|
Следовательно 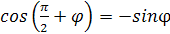 . Поэтому в любом случае
. Поэтому в любом случае 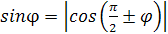 . Применив формулу вычисления косинуса угла между векторами, получим
. Применив формулу вычисления косинуса угла между векторами, получим 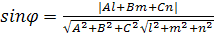 .
.
Условия параллельности и перпендикулярности прямой и плоскости
Пусть прямая задана каноническими уравнениями 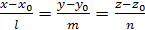 , а плоскость общим уравнением
, а плоскость общим уравнением 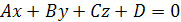 .
.
Прямая и плоскость параллельны тогда и только тогда, когда направляющий вектор прямой  и нормальный вектор плоскости
и нормальный вектор плоскости 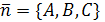 перпендикулярны, то есть их скалярное произведение равно нулю
перпендикулярны, то есть их скалярное произведение равно нулю 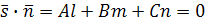 – условие параллельности прямой и плоскости
– условие параллельности прямой и плоскости
Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой 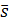 и нормальный вектор
и нормальный вектор  плоскости коллинеарны
плоскости коллинеарны 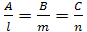 – условие перпендикулярности прямой и плоскости.
– условие перпендикулярности прямой и плоскости.
Окружность
Окружность – это множество точек плоскости, равноудаленных от данной точки (центра).
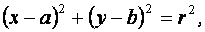 (2)
(2)
где 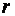 - радиус окружности,
- радиус окружности, 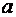 и
и  - координаты центра окружности.
- координаты центра окружности.
Если центр окружности совпадает с началом координат, то уравнение имеет вид
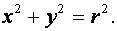 (3)
(3)
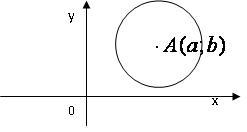
Рис. 2
Эллипс
Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (бóльшая, чем расстояние между фокусами).
Каноническое (простейшее) уравнение эллипса с центром в начале координат и с фокусами в точках 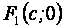 и
и 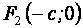 :
:
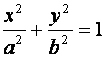 (4)
(4)
где 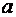 и
и  - полуоси эллипса, с – полуфокусное расстояние. Коэффициенты
- полуоси эллипса, с – полуфокусное расстояние. Коэффициенты 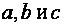 эллипса связаны соотношением
эллипса связаны соотношением 
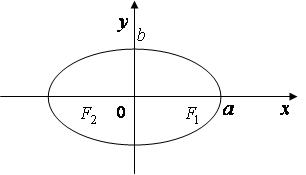
Рис. 3
Если центр эллипса находится в точке 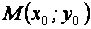 , то уравнение эллипса имеет вид:
, то уравнение эллипса имеет вид:
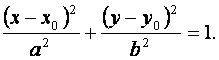 (5)
(5)
Гипербола
Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Уравнение гиперболы с центром в начале координат и с фокусами в точках 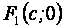 и
и 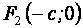 имеет вид:
имеет вид:
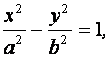 (6)
(6)
где 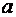 - действительная полуось,
- действительная полуось,
 - мнимая полуось.
- мнимая полуось.
Коэффициенты 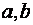 и
и 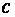 гиперболы связаны соотношением
гиперболы связаны соотношением 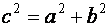 .
.
Прямые 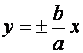 - асимптоты гиперболы.
- асимптоты гиперболы.
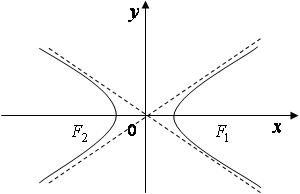
Рис. 4
Если центр гиперболы находится в точке 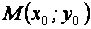 , то уравнение имеет вид:
, то уравнение имеет вид:
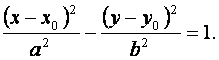 (7)
(7)
Парабола
Параболой называется множество точек плоскости, равноудаленных от точки, называемой фокусом и прямой, называемой директрисой.
Уравнение параболы с вершиной в начале координат имеет вид:
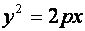 , (8)
, (8)
где 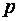 - расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты
- расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты 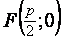 .
.
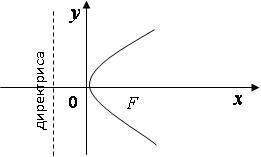
Рис. 5
Если вершина параболы находится в точке 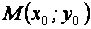 , то уравнение имеет вид:
, то уравнение имеет вид:
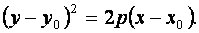
|
из
5.00
|
Обсуждение в статье: Условия параллельности и перпендикулярности прямых |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

