 |
Главная |
Переход от общих уравнений прямой к каноническим или параметрическим уравнениям
|
из
5.00
|
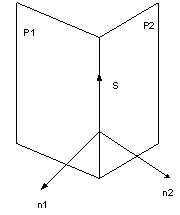
| Для того, чтобы от общих уравнений  перейти к каноническим или параметрическим уравнениям прямой, требуется найти направляющий вектор перейти к каноническим или параметрическим уравнениям прямой, требуется найти направляющий вектор  этой прямой и координаты любой точки этой прямой и координаты любой точки  , принадлежащей ей.
Направляющий вектор прямой ортогонален нормалям , принадлежащей ей.
Направляющий вектор прямой ортогонален нормалям  и и  к обеим плоскостям, следовательно, к обеим плоскостям, следовательно, 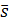 коллинеарен их векторному произведению коллинеарен их векторному произведению  . Поэтому в качестве
направляющего вектора можно выбрать . Поэтому в качестве
направляющего вектора можно выбрать   или любой вектор с пропорциональными координатами. Чтобы найти точку, лежащую на данной прямой, можно задать одну ее координату произвольно, а две остальные
найти из уравнений или любой вектор с пропорциональными координатами. Чтобы найти точку, лежащую на данной прямой, можно задать одну ее координату произвольно, а две остальные
найти из уравнений  , выбрав их так, чтобы определитель из их коэффициентов не равнялся нулю. , выбрав их так, чтобы определитель из их коэффициентов не равнялся нулю.
|
Пример. Составить канонические и параметрические уравнения прямой  .
.
Решение. По условию  ,
,  тогда
тогда 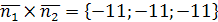 . Следовательно, направляющим вектором прямой можно считать вектор
. Следовательно, направляющим вектором прямой можно считать вектор 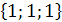 .
.
Будем искать точку на прямой с координатой 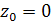 . Для координат
. Для координат  и
и  получим систему уравнений
получим систему уравнений  , откуда
, откуда  ,
,  . Теперь можно составить канонические уравнения прямой:
. Теперь можно составить канонические уравнения прямой:
 .
.
Параметрические уравнения той же прямой имеют вид:
 или
или  .
.
Пример. Привести общие уравнения прямой  к каноническому виду.
к каноническому виду.
Решение. Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, 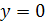 и решив систему уравнений
и решив систему уравнений  найдем
найдем  .
.
Нормальные векторы плоскостей, определяющих прямую, имеют координаты  ,
,  . Поэтому направляющий вектор прямой будет
. Поэтому направляющий вектор прямой будет  . Следовательно,
. Следовательно,  .
.
Замечание. Если какая-либо из координат направляющего вектора равна 0, то предполагается, что для любой точки прямой числитель соответствующей дроби в канонических уравнениях тоже равен 0.
Пусть прямая перпендикулярна одной из координатных осей, например оси  . Тогда направляющий вектор прямой
. Тогда направляющий вектор прямой 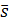 перпендикулярен
перпендикулярен
 , следовательно,
, следовательно,  и параметрические уравнения прямой примут вид
и параметрические уравнения прямой примут вид  . Исключая из уравнений параметр t, получим уравнения прямой в виде
. Исключая из уравнений параметр t, получим уравнения прямой в виде  .
.
Однако, и в этом случае, формально записывают канонические уравнения прямой в виде 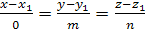 .
.
Таким образом, если в знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Аналогично, каноническим уравнениям  соответствует прямая перпендикулярная осям
соответствует прямая перпендикулярная осям  и
и 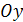 или параллельная оси
или параллельная оси 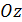 .
.
Пример. Записать уравнение прямой  в параметрическом виде.
в параметрическом виде.
Решение. Обозначим 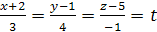 , отсюда
, отсюда 
Пример. Составить канонические и параметрические уравнения прямой, проходящей через точку  параллельно вектору
параллельно вектору  .
.
Решение. Канонические уравнения:  или
или 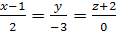 .
.
Параметрические уравнения: 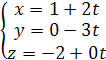 или
или  .
.
Угол между прямыми.
Определение. Углом между прямыми в пространстве называют любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Угол между прямыми в пространстве равен углу между их направляющими векторами 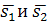 . Поэтому, если две прямые заданы каноническими уравнениями вида
. Поэтому, если две прямые заданы каноническими уравнениями вида  и
и  то косинус угла между ними можно найти по формуле:
то косинус угла между ними можно найти по формуле:
 ).
).
Пример. Найти угол между прямыми 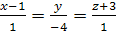 и
и  .
.
Решение. По условию  , тогда
, тогда
 отсюда
отсюда
 ,
,  ,
,  .
.
|
из
5.00
|
Обсуждение в статье: Переход от общих уравнений прямой к каноническим или параметрическим уравнениям |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

