 |
Главная |
Алгоритм решения системы (3.21)–(3.22) симплекс-методом
|
из
5.00
|
Шаг 1.Получение начального решения.
Выбираются т переменных, называемых базисными и обладающих следующим свойством: они входят с коэффициентом 1 только в одно уравнение и с коэффициентом 0 в остальные уравнения системы (3.22).
Остальные п – тпеременных называют свободными.
Все свободные переменные полагаются равными 0, а базисные переменные — равные правым частям соответствующих ограничений системы (3.22).
Пусть т базисных переменных — это переменные x1, x2,...,xm (в противном случае переменные всегда можно перенумеровать).Тогда начальное решение Х0имеет следующий вид:
Хо={x1= b1,х2=b2,...,хт = bm,xm+l = 0,...,хn = 0}.
Если все bi 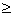 0, то начальное решение является допустимым. Переходят к шагу 3. В противном случае используют алгоритм нахождения начального решения.
0, то начальное решение является допустимым. Переходят к шагу 3. В противном случае используют алгоритм нахождения начального решения.
Шаг 3.Выражение функции f только через свободные переменные.
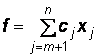
Значения коэффициентов cj, 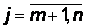 , естественно, отличны от значений коэффициентов в формуле (3.21), но для простоты обозначены той же буквой.)
, естественно, отличны от значений коэффициентов в формуле (3.21), но для простоты обозначены той же буквой.)
Переход к шагу 3.
Шаг 4.Проверка решения на оптимальность.
Составляется симплекс-таблица (табл. 3.3). В левой колонке симплекс-таблицы находятся базисные переменные, в колонке свободных членов – правые части соответствующих ограничений. В i-й строке,
j-м столбце стоит коэффициент при j-й переменной в i-м ограничении (3.22), 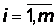 ,
, 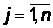 . В последней строке (f – строке) стоит коэффициент с противоположным знаком при j-ой переменной в целевой функции f.
. В последней строке (f – строке) стоит коэффициент с противоположным знаком при j-ой переменной в целевой функции f.
В последнем столбце стоят значения свободных членов, входящего в ограничения.
Таблица 3.3
| Базисные переменные | Коэффициенты при переменных | Свободные члены | |||||||
| x1 | x2 | … | xm | … | xp | … | xn | ||
| x1 x2 … xq … xm | a11 a21 … aq1 … am1 | a11 a22 … aq2 … am2 | …… ... … … … … | a1m a2m … aqm … aAmn | …… ... … … … … | a1p a2p … aqp … amp | …… ... … … … … | a1n a2n … aqn … amn | b1 b2 … bq … bm |
| -f | -c1 | -c2 | -cm | -cp | -cn |
Для проверки решения на оптимальность просматривается последняя f -строка. Если коэффициенты, стоящие при свободных переменных неотрицательны, то полученное решение оптимально. Полученное решение единственно, если все эти коэффициенты положительны. Если среди неотрицательных коэффициентов встречается хотя бы один нулевой, то задача имеет бесконечное множество решений. Если в последней строке есть хотя бы один отрицательный коэффициент, а в соответствующем этому коэффициенту столбце нет ни одного положительного элемента, то целевая функция f не ограничена на области допустимых решений. Если хотя бы один из коэффициентов, стоящих при свободных переменных, отрицательный и в соответствующем ему столбце есть хотя бы положительный элемент, то полученное решение может быть улучшено. Переход к шагу 4.
Шаг 5.Получение нового решения.
Шаг 5.1.Выбор переменной, вводимой в список базисных переменных.
Просматривается последняя строка симплекс-таблицы. Среди элементов этой строки выбирается максимальный по абсолютной величине отрицательный элемент. Столбец, в котором стоит этот элемент, называется разрешающим. Пусть, например, это p-й столбец. Переменная хр,стоящая в этом столбце, вводится в список базисных переменных.
Шаг 5.2.Выбор переменной, выводимой из списка базисных переменных.
Находят отношение элементов столбца свободных членов к элементам разрешающего столбца. При делении на отрицательный элемент и 0 результат полагают равным 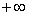 . Среди этих отношений находят минимальное. Строка, соответствующая минимальному отношению, называется разрешающей. Пусть, например, это q-я строка. Базисная переменная xq, стоящая в этой строке, выводится из списка базисных переменных. Элемент симплекс – таблицы aqp, стоящий на пересечении разрешающей строки и разрешающего столбца, называется разрешающим элементом.
. Среди этих отношений находят минимальное. Строка, соответствующая минимальному отношению, называется разрешающей. Пусть, например, это q-я строка. Базисная переменная xq, стоящая в этой строке, выводится из списка базисных переменных. Элемент симплекс – таблицы aqp, стоящий на пересечении разрешающей строки и разрешающего столбца, называется разрешающим элементом.
Шаг 5.3.Выполнение симплекс – преобразования и переход к новой симплекс-таблице.
Элемент aij новой симплекс-таблицы вычисляется с помощью следующего симплекс – преобразования:
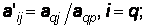 (3.23)
(3.23)
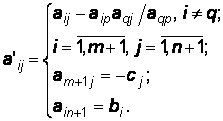 (3.24)
(3.24)
Таким образом, при переходе к новой симплекс-таблице все элементы разрешающей строки делятся на разрешающий элемент (3.23), а все остальные элементы симплекс – таблицы, включая коэффициенты
целевой функции и свободные члены, пересчитываются по формуле (3.24).
Новое решение имеет следующий вид: все свободные переменные в нем полагаются равными 0, а все базисные переменные – свободным членам, стоящим в одной строке с ними.
После построения новой симплекс-таблицы следует перейти к шагу 3
|
из
5.00
|
Обсуждение в статье: Алгоритм решения системы (3.21)–(3.22) симплекс-методом |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

