 |
Главная |
Радиус сходимости и круг сходимости
|
из
5.00
|
Степенным рядом называется ряд вида
 an(z -z0)n, z an(z -z0)n, z  C, z0 C, z0  C, C,
| (32.1) |
числа an  C, n = 1, 2, …, называются коэффициентами ряда (32.1).
C, n = 1, 2, …, называются коэффициентами ряда (32.1).
С помощью замены переменного 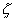 = z - z0 ряд (32.1) может быть преобразован к виду
= z - z0 ряд (32.1) может быть преобразован к виду
 anz n. anz n.
| (32.2) |
Поэтому, как правило, мы ограничиваемся рассмотрением рядов вида (32.2).
Теорема 1 (первая теорема Абеля). Если степенной ряд (32.2) сходится при z = z0, то при любом z таком, что |z| < |z0|, ряд (32.2) сходится абсолютно.
Следствие. Если ряд (32.2) расходится в точке z0, то в любой точке z такой, что |z| > |z0|, он также расходится.
 Если ряд
Если ряд
 an an 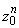
| (32.3) |
сходится, то  an
an 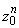 = 0, и потому существует такая постоянная c > 0, что для всех n = 1, 2, … выполняется неравенство
= 0, и потому существует такая постоянная c > 0, что для всех n = 1, 2, … выполняется неравенство
|an 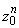 | < c. | < c.
| (32.4) |
 Следовательно, при z0
Следовательно, при z0  0 (в случае z0 = 0 утверждение теоремы очевидно и бессодержательно, так как множество таких z, что |z| < 0, пусто) имеем
0 (в случае z0 = 0 утверждение теоремы очевидно и бессодержательно, так как множество таких z, что |z| < 0, пусто) имеем
anzn| = |an 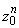 ||z|/|z0|n
||z|/|z0|n  c|z|/|z0|n, и если |z| < |z0|, то ряд
c|z|/|z0|n, и если |z| < |z0|, то ряд  |z|/|z0|n сходится, ибо является суммой бесконечно убывающей геометрической прогрессии (ее знаменатель |z|/|z0|n = |z|/|z0| < 1). Поэтому по признаку сравнения сходимости рядов из неравенства (32.5) следует, что сходится ряд
|z|/|z0|n сходится, ибо является суммой бесконечно убывающей геометрической прогрессии (ее знаменатель |z|/|z0|n = |z|/|z0| < 1). Поэтому по признаку сравнения сходимости рядов из неравенства (32.5) следует, что сходится ряд  |anzn|, т. е. ряд (32.2) абсолютно сходится (рис. 127).
|anzn|, т. е. ряд (32.2) абсолютно сходится (рис. 127). 
Следствие сразу вытекает из теоремы: если в точке z0 ряд (32.2) расходится, то при |z| > |z0| он не может сходиться в точке z, так как тогда бы он по доказанной теореме сходился (и даже абсолютно) в точке z0.
Рассмотрим степенной ряд (32.2). Он заведомо сходится в точке z = 0. Обозначим через X множество всех таких действительных неотрицательных чисел x  R, что при z = x ряд (32.2) сходится. Поскольку 0
R, что при z = x ряд (32.2) сходится. Поскольку 0  X, то
X, то
X 
 . Пусть
. Пусть
| R = sup X. | (32.6) |
Очевидно, 0 < R < + 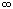 . Неравенство |z| < R задает на комплексной плоскости C замкнутый круг радиуса R с центром в точке z = 0. При R = 0 этот круг вырождается в точку z = 0, а приR = +
. Неравенство |z| < R задает на комплексной плоскости C замкнутый круг радиуса R с центром в точке z = 0. При R = 0 этот круг вырождается в точку z = 0, а приR = + 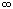 превращается во всю комплексную плоскость.
превращается во всю комплексную плоскость.
Определение 1. Число R = sup X (конечное или бесконечное) называется радиусом сходимости ряда} (32.2), а круг {z: |z| < R} - его кругом сходимости.
Теорема 2. Пусть R - радиус сходимости ряда (32.2). Тогда если |z| < R, то ряд (32.2) сходится абсолютно, если |z| > R, то ряд (32.2) расходится, а если 0 < r < R, то в круге{z: |z| < r} ряд (32.2) сходится равномерно.
 Если R = 0, то точек z
Если R = 0, то точек z  C таких, что |z| < R нет. Если же 0 < R < +
C таких, что |z| < R нет. Если же 0 < R < + 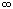 и z
и z  C таково, что |z| < R, то согласно определению верхней грани из равенства R = sup X следует, что существует такое x
C таково, что |z| < R, то согласно определению верхней грани из равенства R = sup X следует, что существует такое x  X, что |z| < x < R, а так как по определению множества X во всех его точках x ряд
X, что |z| < x < R, а так как по определению множества X во всех его точках x ряд  an xn сходится, то по первой теореме Абеля он абсолютно сходится в точке z.
an xn сходится, то по первой теореме Абеля он абсолютно сходится в точке z.
 Рис. 128 Рис. 128
|
Если R = + 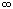 , то точек z
, то точек z  C таких, что |z| > R, нет. Если же R < +
C таких, что |z| > R, нет. Если же R < + 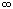 и z
и z  C таково, что |z| > R, то для любой точки x такой, что R < x < |z|, согласно определению R = sup X имеем x
C таково, что |z| > R, то для любой точки x такой, что R < x < |z|, согласно определению R = sup X имеем x 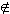 X, а поэтому в силу определения множества X ряд
X, а поэтому в силу определения множества X ряд  an xn расходится. Следовательно, в силу следствия из теоремы 1 ряд (32.2) расходится в рассматриваемой точке z.
an xn расходится. Следовательно, в силу следствия из теоремы 1 ряд (32.2) расходится в рассматриваемой точке z.
Если теперь
| 0 < r < R, | (32.7) |
то покажем, что ряд (32.2) сходится равномерно в круге |z| < r (рис. 128). Действительно, если |z| < r, то
| |anzn| < |anrn|. | (32.8) |
Из неравенства (32.7), согласно вышедоказанному свойству радиуса сходимости, вытекает, что ряд (32.2) при z = r абсолютно сходится, т. е. сходится ряд  |anrn, а тогда в силу признака равномерной сходимости Вейерштрасса (п. 31.2) из неравенства (32.8) следует, что ряд (32.2) равномерно сходится в круге {z: |z| < r}.
|anrn, а тогда в силу признака равномерной сходимости Вейерштрасса (п. 31.2) из неравенства (32.8) следует, что ряд (32.2) равномерно сходится в круге {z: |z| < r}. 
Рассмотрим степенной ряд общего вида  an(z - z0)n. Он сходится или расходится в точке z тогда и только тогда, когда соответственно сходится или расходится в точке
an(z - z0)n. Он сходится или расходится в точке z тогда и только тогда, когда соответственно сходится или расходится в точке 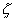 = z - z0ряд
= z - z0ряд  an
an  . Радиус сходимости R последнего ряда называется и радиусом сходимости исходного ряда
. Радиус сходимости R последнего ряда называется и радиусом сходимости исходного ряда  an (z - z0)n
an (z - z0)n
При замене переменного 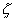 = z - z0 кругу сходимости {
= z - z0 кругу сходимости { 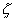 : |
: | 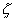 | < R} ряда
| < R} ряда  an
an  соответствует круг {z: |z - z0| < R}. Он называется кругом сходимости ряда
соответствует круг {z: |z - z0| < R}. Он называется кругом сходимости ряда  an(z - z0)n.
an(z - z0)n.
Из теоремы 2 следует, что если R является радиусом сходимости ряда  an(z - z0)n, то при |z - z0| < R этот ряд абсолютно сходится, при |z - z0| > R он расходится, а если 0 < r < R, то в круге{z: |z - z0| < r} ряд равномерно сходится.
an(z - z0)n, то при |z - z0| < R этот ряд абсолютно сходится, при |z - z0| > R он расходится, а если 0 < r < R, то в круге{z: |z - z0| < r} ряд равномерно сходится.
Отметим, что из равномерной сходимости ряда (32.1) в любом круге |z - z0| < R, где 0 < r < R$, и непрерывности каждого члена этого ряда следует, что сумма каждого степенного ряда непрерывна внутри его круга сходимости R > 0.
Действительно, для любого z, |z| < R, можно выбрать такое R, что |z| < r < R. В круге |z| < r рассматриваемый ряд сходится равномерно, а так как его члены - непрерывные функции, то его сумма также непрерывна на этом круге, в частности в точке z (см. теорему 7 в п. 31.4).
Примеры.
1. Рассмотрим ряд
 n!zn. n!zn.
| 32.9 |
Для исследования его абсолютной сходимости применим признак Даламбера (п. 30.4):
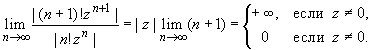
Следовательно, ряд (32.9) сходится только при z = 0, а потому его радиус сходимости равен нулю: R = 0.
2. Радиус сходимости R ряда
 zn/n! zn/n!
| (32.10) |
равен + 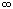 , так как в п. 31.1 было показано, что этот ряд сходится при любом z
, так как в п. 31.1 было показано, что этот ряд сходится при любом z  C.
C.
3. Радиус сходимости суммы бесконечной геометрической прогрессии
 zn zn
| (32.11) |
равен 1, так как ряд (32.11) сходится при |z| < 1 и расходится при |z| > 1 (п. 30.1, 30.2). На границе {z: |z| = 1} круга сходимости имеем |z| = 1 и, следовательно, последовательность членов ряда (32.11) не стремится к нулю, откуда явствует, что во всех точках границы своего круга сходимости ряд (32.11) расходится.
4. У ряда
 zn/n2 zn/n2
| (32.12) |
радиус сходимости также равен 1. Действительно, при |z| < 1 выполняется неравенство
| |zn/n2| < 1/n2 | (32.13) |
и, следовательно, согласно признаку равномерной сходимости Вейерштрасса, ряд (32.12) равномерно, а следовательно, и просто сходится. При |z| > 1 имеем  |zn|/n2 = +
|zn|/n2 = + 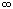 , т. е. не выполняется необходимое условие сходимости ряда (см. теорему 1 из п. 30.2), и, таким образом, ряд (32.12) при |z| > 1 расходится.
, т. е. не выполняется необходимое условие сходимости ряда (см. теорему 1 из п. 30.2), и, таким образом, ряд (32.12) при |z| > 1 расходится.
Отметим, что во всех точках границы круга сходимости, т. е. при |z| = 1, в силу того же неравенства (32.13) ряд (32.12) сходится.
5. Радиус сходимости R ряда
 zn/n zn/n
| (32.14) |
можно найти, применив признак Даламбера: имеем

Поэтому ряд (32.14) сходится при |z| < 1 и расходится при |z| > 1. Таким образом, R = 1.
В точке z = 1 границы круга сходимости ряд (32.14) превращается в гармонический ряд и, следовательно, расходится, а при z = -1 получается сходящийся ряд  (-1)n/n. Итак, у ряда (32.14) на границе круга сходимости имеются как точки, в которых он сходится, так и точки, в которых он расходится. Разобранные примеры показывают, что существуют степенные ряды, у которых радиус сходимости равен нулю (ряд (32.9)), равен конечному положительному числу (ряд (32.11)) и равен бесконечности (ряд (32.10)). На границе круга сходимости ряд может во всех точках сходиться (ряд (32.12)), а может и сходиться в одних точках и расходиться в других (ряд (32.14)) или расходиться во всех точках (ряд (32.11)).
(-1)n/n. Итак, у ряда (32.14) на границе круга сходимости имеются как точки, в которых он сходится, так и точки, в которых он расходится. Разобранные примеры показывают, что существуют степенные ряды, у которых радиус сходимости равен нулю (ряд (32.9)), равен конечному положительному числу (ряд (32.11)) и равен бесконечности (ряд (32.10)). На границе круга сходимости ряд может во всех точках сходиться (ряд (32.12)), а может и сходиться в одних точках и расходиться в других (ряд (32.14)) или расходиться во всех точках (ряд (32.11)).
Функции, раскладывающиеся в степенные ряды, называются аналитическими. Точнее, имеет место следующее
Определение 2. Функция f называется аналитической в точке z0, если в некоторой окрестности (см. п. 5.11) этой точки функция f раскладывается в степенной ряд:
f(z) =  an(z - z0)n.
an(z - z0)n.
Поскольку в силу определения окрестности точки все точки, достаточно близкие к данной точке, принадлежат ее окрестности, то радиус сходимости написанного ряда положителен.
Теорема 3* (вторая теорема Абеля). Если R - радиус сходимости степенного ряда (32.2), R < + 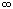 , и этот ряд сходится при z = R, то он сходится равномерно на отрезке [0,R]действительной оси.
, и этот ряд сходится при z = R, то он сходится равномерно на отрезке [0,R]действительной оси.
Следствие. Если ряд (32.2) сходится при z = R, то его сумма непрерывна на отрезке [0,R] действительной оси.
 Доказательство теоремы. Имеем
Доказательство теоремы. Имеем
 anxn= \ anxn= \  anRn(x/R)n, anRn(x/R)n,
| (32.15) |
причем, по условию теоремы ряд  anRn сходится. Поскольку этот ряд числовой, то его сходимость можно рассматривать как равномерную сходимость на отрезке [0,R]. Последовательность
anRn сходится. Поскольку этот ряд числовой, то его сходимость можно рассматривать как равномерную сходимость на отрезке [0,R]. Последовательность
(x/R)n, n = 1, 2, ...,
ограничена на отрезке [0,R], ибо если 0 < x < R, то
0 < (x/R)n < 1,
и монотонна при любом x  [0,R]. Следовательно, в силу признака равномерной сходимости Абеля (п. 31.3*) ряд (32.2) равномерно сходится на отрезке [0,R].
[0,R]. Следовательно, в силу признака равномерной сходимости Абеля (п. 31.3*) ряд (32.2) равномерно сходится на отрезке [0,R]. 
Утверждение следствия вытекает из непрерывности каждого члена ряда (32.2) на отрезке [0,R] и доказанной равномерной сходимости этого ряда на указанном отрезке. Докажем еще одну лемму для степенных рядов в комплексной области, которая будет использована в следующем параграфе.
Лемма 1. Радиусы сходимости R, R1 и R2 соответственно рядов
 anzn, anzn,
| (32.16) |
  zn+1, zn+1,
| (32.17) |
 nanzn-1 nanzn-1
| (32.18) |
равны:
| R = R1 = R2. | (32.19) |
Таким образом, ряды (32.17) и (32.18), получающиеся из (32.16) соответственно с помощью "формального интегрирования и дифференцирования", имеют те же радиусы сходимости, что и исходный ряд. Интегрирование и дифференцирование названо здесь формальным, поскольку для функций комплексного аргумента эти операции у нас не были определены и они были произведены так, как если бы an и z были действительными числами.
 Из неравенства
Из неравенства

 zn+1
zn+1  =
=  |z||anzn| < |z||anzn|
|z||anzn| < |z||anzn|
следует, что если в точке z абсолютно сходится ряд (32.16), то в этой точке абсолютно сходится и ряд (32.17), а это означает, что радиус сходимости R1 ряда (32.17) не меньше радиуса сходимости R ряда (32.16): R1 > R. Из неравенства же
|anzn| < n|anzn| = |nanzn-1||z|
следует, что если в точке z абсолютно сходится ряд (32.18), то в этой точке абсолютно сходится и ряд (32.16), т. е. R > R2.
Таким образом,
| R1 > R > R2. | (32.20) |
Покажем теперь, что
| R2 > R1. | (32.21) |
Возьмем какую-либо точку z  0 внутри круга сходимости ряда (32.17) и докажем, что в ней сходится ряд (32.18). Поскольку |z| < R1, то существует такое действительное число R, что
0 внутри круга сходимости ряда (32.17) и докажем, что в ней сходится ряд (32.18). Поскольку |z| < R1, то существует такое действительное число R, что
| |z| < r < R1. | (32.22) |
Запишем абсолютную величину члена ряда (32.18) следующим образом:
|nanzn-1| =     rn+1 rn+1  . .
| (32.23) |
Положим q = |z/r|. В силу условия (32.22) 0 < q < 1. Ряд


 =
= 
 qn+1
qn+1
сходится (в этом легко убедиться, например, с помощью признака Даламбера). Поэтому последовательность его членов стремится к нулю и, следовательно, ограничена, т. е. существует такая постоянная c > 0, что для всех n = 0, 1, 2, ... выполняется неравенство
  qn+1 qn+1  < c. < c.
| (32.24) |
Из (32.23) и (32.24) следует неравенство
|nanzn-1|< c 
 rn+1
rn+1  .
.
Поскольку r  R1, то ряд
R1, то ряд 
 rn+1 абсолютно сходится, т. е. сходится ряд
rn+1 абсолютно сходится, т. е. сходится ряд 

 rn+1
rn+1  , а поэтому по признаку сравнения сходится и ряд
, а поэтому по признаку сравнения сходится и ряд  nanzn-1. Итак, из условия |z| < R1, следует абсолютная сходимость ряда (32.18). Это и означает выполнение неравенства (32.21). Из неравенств (32.20) и (32.21) следует, что имеет место равенство (32.19).
nanzn-1. Итак, из условия |z| < R1, следует абсолютная сходимость ряда (32.18). Это и означает выполнение неравенства (32.21). Из неравенств (32.20) и (32.21) следует, что имеет место равенство (32.19). 
|
из
5.00
|
Обсуждение в статье: Радиус сходимости и круг сходимости |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

