 |
Главная |
Лабораторная работа №2. Министерство образования и науки РФ
|
из
5.00
|
Министерство образования и науки РФ
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Ульяновский государственный педагогический университет
Им. И.Н. Ульянова»
ЧИСЛЕННЫЕ МЕТОДЫ
Методические разработки для студентов
Физико-математического факультета
Ульяновск, 2010
Лабораторная работа №1
Элементарная теория погрешностей
Краткая теория
Пусть x - точное значение числа, а – его приближенное значение. Тогда разность х-а называют погрешностью числа а. Эта погрешность может быть положительной (если а - приближение по недостатку) и отрицательной (если а – приближение по избытку). Удобнее бывает вычислить абсолютную величину этой разности:
Δ=|х-а|.
Число Δ называют абсолютной погрешностью числа а. Если точное значение числа неизвестно, то вычислить абсолютную погрешность его приближения невозможно. Тогда величину абсолютной погрешности оценивают сверху:
|х-а| ≤Δа.
Наименьшее из чисел Δа, которое удается получить, называется предельной абсолютной погрешностью числа а.
Относительной погрешностью числа а называют отношение абсолютной погрешности к точному значению числа (или, если точное значение не известно, к приближенному значению):
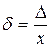 или
или 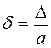 .
.
Предельной абсолютной погрешностью числа а называют отношение его предельной абсолютной погрешности к точному (или приближенному) значению числа:
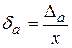 или
или 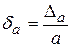 .
.
Цифра приближенного числа называется верной в широком (узком) смысле, если предельная абсолютная погрешность числа не превосходит единицы (половины единицы) разряда, в котором находится эта цифра.
Значащими называются все верные цифры приближенного числа, кроме нулей, стоящих слева от первой ненулевой цифры.
Связь между количеством верных цифр приближенного числа и его предельной относительной погрешностью отражается формулами:
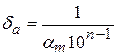 - в широком смысле,
- в широком смысле, 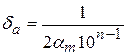 - в узком смысле,
- в узком смысле,
где 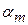 - старшая значащая цифра числа , n –количество значащих цифр.
- старшая значащая цифра числа , n –количество значащих цифр.
Решение одного варианта
1.Определить, какое равенство точнее:
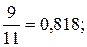
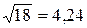 .
.
Находим значение данных выражений с большим числом десятичных знаков:
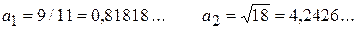
Затем вычислим предельные абсолютные погрешности, округляя их с избытком:
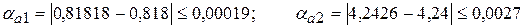
Предельные относительные погрешности составляют:
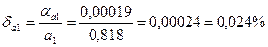
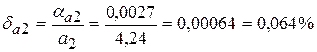
Так как 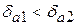 , то равенство
, то равенство 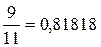 является более точным.
является более точным.
2. Округлить сомнительные цифры числа, оставив верные знаки
а) в узком смысле; б) в широком смысле.
Определить абсолютную погрешность результата.
а) 72,353( 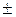 0,026); б) 2,3544;
0,026); б) 2,3544; 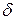 =0,2%
=0,2%
а) Пусть а=72,353( 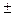 0,026). По определению погрешность
0,026). По определению погрешность
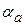 =0,026<5.
=0,026<5.
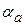 =0,026<0,5.
=0,026<0,5.
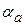 =0,026<0,05. Но
=0,026<0,05. Но 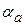 =0,026>0,005.
=0,026>0,005.
Это означает, что в числе 72,353 верными в узком смысле являются цифры 7,2,3.
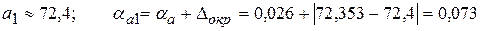
Полученная погрешность 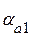 больше 0,05. Значит, нужно уменьшить количество цифр в приближенном числе до двух:
больше 0,05. Значит, нужно уменьшить количество цифр в приближенном числе до двух:
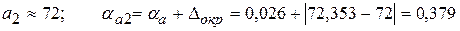
Так как 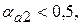 то обе оставшиеся цифры верны в узком смысле.
то обе оставшиеся цифры верны в узком смысле.
б) Пусть a= 2,3544; 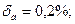 тогда
тогда 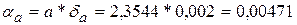 .
.
По определению погрешности
αа=0,00471<1.
αа=0,00471<0,1.
αа=0,00471<0,01. Но αа=0,00471>0,001.
Это означает, что верными в широком смысле являются три цифры (2, 3, 5). По правилам округления найдем приближенное значение числа, сохранив десятичные доли.
а1 ≈2,35; αа=0,0044+0,00471=0,00911<0,01
Значит, и в округленном числе 2,35 все три цифры верны в широком смысле.
3.Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры
а) в узком смысле; б) в широком смысле.
а) Так как все четыре цифры числа а=0,4357 верны в узком смысле, то абсолютная погрешность αа=0.00005, а относительная погрешность:
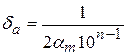 , где αm=4, n=4
, где αm=4, n=4 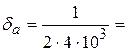 0,000125=0,0125%
0,000125=0,0125%
б) Так как все пять цифр числа а=12,384 верны в широком смысле, то αа=0,001;
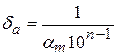 , где αm=1, n=5
, где αm=1, n=5 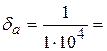 0,0001=0,01%
0,0001=0,01%
Задания
1)Определить, какое равенство точнее.
2) Округлить сомнительные цифры числа, оставив верные знаки а) в узком смысле; б) в широком смысле. Определить абсолютную погрешность результата.
3)Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры а) в узком смысле; б) в широком смысле.
Вариант 1
1) 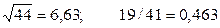 2) a)22,553(±0,016);
б)2,8546; δ=0,3%
3) а)0,2387; б) 42,884
Вариант 3
1)
2) a)22,553(±0,016);
б)2,8546; δ=0,3%
3) а)0,2387; б) 42,884
Вариант 3
1)  2) a)0,5748(±0,0034);
б)34,834; δ=0,1%
3) а)11,445; б) 2,043
Вариант 5
1)6/7=0,857;
2) a)0,5748(±0,0034);
б)34,834; δ=0,1%
3) а)11,445; б) 2,043
Вариант 5
1)6/7=0,857; 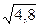 =2,19
2) a)5,435(±0,0028)
б)10,8441 δ=0,5%
3) а)8,345; б) 0,288
Вариант 7
1)2/21=0,095; =2,19
2) a)5,435(±0,0028)
б)10,8441 δ=0,5%
3) а)8,345; б) 0,288
Вариант 7
1)2/21=0,095; 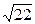 =4,69
2) a)2,4543(±0,0032)
б)24,5643; δ=0,1%
3) а)0,374; б) 4,348
Вариант 9
1)6/11=0,545; =4,69
2) a)2,4543(±0,0032)
б)24,5643; δ=0,1%
3) а)0,374; б) 4,348
Вариант 9
1)6/11=0,545; 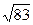 =9,11
2) a)3,7834(±0,0041)
б)21,68563; δ=0,3%
3) а)41,72; б) 0,678
Вариант 11
1)21/29=0,723; =9,11
2) a)3,7834(±0,0041)
б)21,68563; δ=0,3%
3) а)41,72; б) 0,678
Вариант 11
1)21/29=0,723; 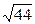 =6,63
2) a)13,6253(±0,0021)
б)0,3567; δ=0,042%
3) а)18,357; б) 2,16
Вариант 13
1)13/17=0,764; =6,63
2) a)13,6253(±0,0021)
б)0,3567; δ=0,042%
3) а)18,357; б) 2,16
Вариант 13
1)13/17=0,764; 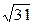 =5,56
2) a)3,6878(±0,0013)
б)15,873; δ=0,42%
3) а)14,862; б) 8,7
Вариант 15
1)6/11=0,545; =5,56
2) a)3,6878(±0,0013)
б)15,873; δ=0,42%
3) а)14,862; б) 8,7
Вариант 15
1)6/11=0,545; 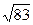 =9,11
2) a)3,7834(±0,0041)
б)21,68563; δ=0,3%
3) а)41,72; б) 0,678
Вариант 17
1)49/13=3,77; =9,11
2) a)3,7834(±0,0041)
б)21,68563; δ=0,3%
3) а)41,72; б) 0,678
Вариант 17
1)49/13=3,77; 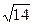 =3,74
2) a)5,6483(±0,0017)
б)83,736; δ=0,085%
3) а)5,3462; б) 0,00858
Вариант 19
1)19/12=1,58; =3,74
2) a)5,6483(±0,0017)
б)83,736; δ=0,085%
3) а)5,3462; б) 0,00858
Вариант 19
1)19/12=1,58; 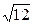 =3,46
2) a)4,88445(±0,00052)
б) 0,096835; δ=0,32%
3) а)12,688; б) 4,636
Вариант 21
1)18/7=2,57; =3,46
2) a)4,88445(±0,00052)
б) 0,096835; δ=0,32%
3) а)12,688; б) 4,636
Вариант 21
1)18/7=2,57; 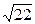 =4,69
2) a)0,39642(±0,00022)
б)46,453; δ=0,15%
3) а)15,644; б) 6,125
Вариант 23
1) 16/7=2,28; =4,69
2) a)0,39642(±0,00022)
б)46,453; δ=0,15%
3) а)15,644; б) 6,125
Вариант 23
1) 16/7=2,28; 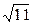 =3,32
2) a)0,75244(±0,00013)
б)24,3872; δ=0,34%
3) а)16,383; б) 5,734
Вариант 25
1)12/7=1,71; =3,32
2) a)0,75244(±0,00013)
б)24,3872; δ=0,34%
3) а)16,383; б) 5,734
Вариант 25
1)12/7=1,71; 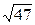 =6,86
2) a)0,38725(±0,00112)
б)72,354; δ=0,24%
3) а) 18,275; б) 0,00644
Вариант 27
1)23/9=2,56; =6,86
2) a)0,38725(±0,00112)
б)72,354; δ=0,24%
3) а) 18,275; б) 0,00644
Вариант 27
1)23/9=2,56; 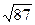 =9,33
2) a)4,57633(±0,00042)
б)23,7564; δ=0,44%
3) а) 3,75; б) 6,8343 =9,33
2) a)4,57633(±0,00042)
б)23,7564; δ=0,44%
3) а) 3,75; б) 6,8343
| Вариант 2
1)7/15=0,467; 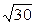 =5,48
2) a)6,4257(±0,0024)
б)17,2834; δ=0,3%
3) а)3,751; б) 0,537
Вариант 4
1)15/7=2,14; =5,48
2) a)6,4257(±0,0024)
б)17,2834; δ=0,3%
3) а)3,751; б) 0,537
Вариант 4
1)15/7=2,14; 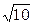 =3,16
2) a)2,3485(±0,0042)
б)0,34484; δ=0,4%
3) а)2,3445; б) 0,745
Вариант 6
1)12/11=1,091; =3,16
2) a)2,3485(±0,0042)
б)0,34484; δ=0,4%
3) а)2,3445; б) 0,745
Вариант 6
1)12/11=1,091; 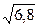 =2,61
2) a)0,12356(±0,00036)
б)8,24163; δ=0,2%
3) а) 12,45; б) 3,4453
Вариант 8
1)23/15=1,53; =2,61
2) a)0,12356(±0,00036)
б)8,24163; δ=0,2%
3) а) 12,45; б) 3,4453
Вариант 8
1)23/15=1,53; 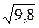 =3,13
2) a)8,3445(±0,0022)
б)23,574; δ=0,2%
3) а)20,43; б) 0,576
Вариант 10
1)17/19=0,889; =3,13
2) a)8,3445(±0,0022)
б)23,574; δ=0,2%
3) а)20,43; б) 0,576
Вариант 10
1)17/19=0,889; 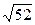 =7,21
2) a)13,537(±0,0026)
б)7,521; δ=0,12%
3) а)5,634; б) 0,0748
Вариант 12
1)50/19=2,63; =7,21
2) a)13,537(±0,0026)
б)7,521; δ=0,12%
3) а)5,634; б) 0,0748
Вариант 12
1)50/19=2,63; 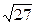 =5,19
2) a)1,784(±0,0063)
б)0,85637; δ=0,21%
3) а)0,5746; б) 236,58
Вариант 14
1)7/22=0,318; =5,19
2) a)1,784(±0,0063)
б)0,85637; δ=0,21%
3) а)0,5746; б) 236,58
Вариант 14
1)7/22=0,318; 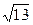 =3,60
2) a)27,1548(±0,0016)
б)0,3945; δ=0,16%
3) а)0,3648; б)21,7
Вариант 16
1)5/3=1,667; =3,60
2) a)27,1548(±0,0016)
б)0,3945; δ=0,16%
3) а)0,3648; б)21,7
Вариант 16
1)5/3=1,667; 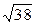 =6,16
2) a)0,98351(±0,00042)
б)3,7542; δ=0,32%
3) а)62,74; б) 0,389
Вариант 18
1)3/7=1,857; =6,16
2) a)0,98351(±0,00042)
б)3,7542; δ=0,32%
3) а)62,74; б) 0,389
Вариант 18
1)3/7=1,857; 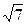 =2,64
2) a)32,7486(±0,0012)
б)2,8867; δ=0,43%
3) а)0,0384; б) 63,745
Вариант 20
1)51/11=4,64; =2,64
2) a)32,7486(±0,0012)
б)2,8867; δ=0,43%
3) а)0,0384; б) 63,745
Вариант 20
1)51/11=4,64; 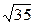 =5,91
2) a)38,4258(±0,0014)
б)0,66385; δ=0,34%
3) а)6,743; б) 0,543
Вариант 22
1)17/9=2,11; =5,91
2) a)38,4258(±0,0014)
б)0,66385; δ=0,34%
3) а)6,743; б) 0,543
Вариант 22
1)17/9=2,11; 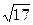 =4,12
2) a)0,66385(±0,00042)
б)5,8425; δ=0,23%
3) а)0,3825; б) 24,6
Вариант 24
1)21/13=1,54; =4,12
2) a)0,66385(±0,00042)
б)5,8425; δ=0,23%
3) а)0,3825; б) 24,6
Вариант 24
1)21/13=1,54; 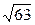 =7,94
2) a)2,3684(±0,0017)
б)45,7832; δ=0,18%
3) а)0,573; б) 3,6761
Вариант 26
1)6/7=0,857; =7,94
2) a)2,3684(±0,0017)
б)45,7832; δ=0,18%
3) а)0,573; б) 3,6761
Вариант 26
1)6/7=0,857; 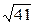 =6,40
2) a)0,36127(±0,00034)
б)46,7843; δ=0,32%
3) а) 3,425; б) 7,38
Вариант 28
1)27/31=0,872; =6,40
2) a)0,36127(±0,00034)
б)46,7843; δ=0,32%
3) а) 3,425; б) 7,38
Вариант 28
1)27/31=0,872; 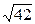 =6,48
2) a)15,8372(±0,0026)
б)0,088748; δ=0,56%
3) а) 3,643; б) 72,385 =6,48
2) a)15,8372(±0,0026)
б)0,088748; δ=0,56%
3) а) 3,643; б) 72,385
|
Лабораторная работа №2
|
из
5.00
|
Обсуждение в статье: Лабораторная работа №2. Министерство образования и науки РФ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

