Метод половинного деления. Один из методов уточнения корней уравнения (1) – метод половинного деления

Один из методов уточнения корней уравнения (1) – метод половинного деления. Исходные данные: уравнение f(x)=0; отрезок [a,b], на котором существует единственный корень уравнения (корень отделен), т.е. f(x) удовлетворяет условиям: f(x) непрерывна на [a,b], монотонна нем и f(a)f(b)<0 (2).

 

Алгоритм метода

1. Найти середину отрезка [a,b] ; c=(a+b)/2.

2. Если f(c)=0, то с - точный корень и процесс заканчивается.

3. Иначе если f(a)f(c)>0 (знаки функции f(x) в точках a и c одинаковы), то левый конец отрезка заменяется на середину (а=с) иначе правый конец заменяется на середину (b=c).

4. Если длина отрезка не превосходит заданной точности (b-a<=ε), то x=c и процесс заканчивается, иначе идти к п.1.

 

Решение одного варианта

1. Отделить корни аналитически и уточнить их методом половинного деления с точностью до 0.01: x⁴-x³-2x²+3x-3=0.

Полагая f(x)= x⁴-x³-2x²+3x-3, имеем f’(x)=4x³-3x²-4x+3.

Найдем нули производной: 4x³-3x²-4x+3=0; 4x(x²-1)-3(x²-1)=0;(x²-1)(4x-3)=0;

x₁=-1; x₂=1; x₃=3/4.

Составим таблицу знаков функции f(x):

x	-∞	-1	3/4		+∞
f(x)	+	-	-	-	+

Из таблицы видно, что уравнение имеет два действительных корня x₁ (-∞;-1) и x₂ (1;+ ∞). Уменьшим промежутки, на которых находятся корни, до единичной длины:

x	-2	-1
f(x)	+	-	-	+

Следовательно, x₁ (-2;-1) и x₂ (1;2).

Уточним один из корней, например, x₁, методом половинного деления до сотых долей. Все вычисления удобно производить, используя следующую таблицу:

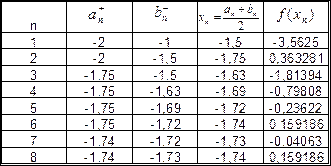
x₁≈-1,73.

Второй корень, уточняемый аналогичным образом, равен 1,73.

2. Отделить корни графически и уточнить их методом половинного деления.

Перепишем уравнение в виде . Обозначим , и построим графики этих функций:

Из рисунка видно, что уравнение имеет три корня: точный x=0 и еще два, расположенных симметрично на отрезках [-3;-2] и [2;3].

Уточним корень на отрезке [2;3]:

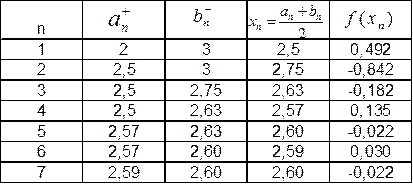
Ответ: x₁=0, x₂=2,59, x₃=-2,59.

 

Задания

1)Отделить корни аналитически и уточнить их методом половинного деления до 0,01, используя электронные таблицы.

1. 3x⁴+4x³-12x²-5=0

2. 2x³-9x²-60x+1=0

3. x⁴-2x-1=0

4. 2x⁴-x²-10=0

5. 3x⁴+3x³+6x²-10=0

6. x⁴-18x²+6=0

7. x⁴+4x³-3x²-17=0

8. x⁴-x³-2x²+3x-3=0

9. 3x⁴+4x³-12x²+1=0

10. 3x⁴-8x³-18x²+2=0

11. 2x⁴-3x³+8x²-1=0

12. 2x⁴+8x³+3x²-1=0

13. x⁴-4x³-8x²+1=0

14. 3x⁴+4x³-12x²-5=0

15. 2x³-8x²-30x+1=0

16. x⁴-30x-2=0

17. 2x⁴-2x²-7=0

18. 3x⁴+8x³+6x²-10=0

19. x⁴-18x²+6=0

20. x⁴+4x³-3x-7=0

21. x⁴-2x³-x²+3x-3=0

22. 3x⁴+4x³-3x²-17=0

23. 2x⁴-5x³-12x²+2=0

24. 3x⁴+9x³-14x²+1=0

25. x⁴+2x³-x-1=0

26. x⁴+8x³-6x²-72x=0

27. x⁵-x-0,2=0

28. x⁴-3x²+75x-10000=0

2) Отделить корни графически и уточнить их методом половинного деления до 0.01, используя электронные таблицы.

1. (x-3)cosx=1

2. sin(x+π/3)-0.5x=0

3. (x-1)²lg(x+11)=1

4. cos(x+0.5)=x³

5. 5sinx=x-1

6. tg³x=x

7. x²cos2x=-1

8. xlg(x+1)=1

9. x²-20sinx=0

10. 2lgx-x/2+1=0

11. (x-2)cosx=1

12. sin(x-0.5)-x+0.5=0

13. x²-20sinx=0

14. cos(x+0.3)=x²

15. 5sinx=x=1

16. tg²x=x

17. x²sin2x=1

18. xlg(x+2)=1

19. x²-10sinx=0

20. 2lgx-x/2+1=0

21. (x-5)cosx=-1

22. sin(x+5)=0.5x

23. x²lg(x=7)=1

24. cos(x-0.5)=x²

25. (0,2х)³=сosx

26. x-10sinx=0

27. 2lg(x+7)-5sinx=0

28. 1.2-lnx=4cos2x

Лабораторная работа №3

Решение нелинейных уравнений методом хорд

Краткая теория

Будем рассматривать уравнения вида f(x)=0 (1). Пусть корень уравнения отделен и находится на отрезке [a,b]. Уточним этот корень методом хорд. Геометрически метод хорд означает замену на отрезке [a,b] графика функции y=f(x) хордой, проведенной через точки (a,f(a)) и (b,f(b)):

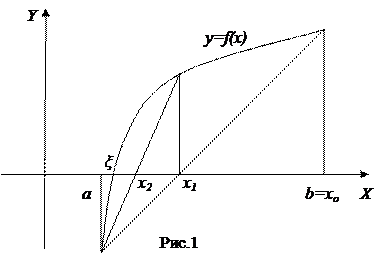
Здесь ξ - точный корень уравнения (1), ­­x - начальное приближение к корню, x -точка пересечения хорды с осью Ох – первое приближение к корню. Далее метод хорд применяется на отрезке [a, x ] и получается второе приближение к корню - x . В случае, изображенном на рис.1, конец отрезка а остается неподвижным. Из уравнения хорды и условия, что точка (x ,0) принадлежит хорде, получается формула для вычисления n-го приближения к корню для случая, когда а – неподвижный конец: x =b,

x =a- (2)

Для случая неподвижного конца b используется формула: x =a,

x =x - (3)

 

Правило определения неподвижного конца хорды:

Если знаки первой и второй производных функции f(x) на отрезке [a, b] совпадают, то неподвижным являются конец b, иначе - конец a.

 

Погрешность метода

Метод хорд обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1), не превосходящую длину n-го отрезка:

 

Алгоритм метода

1. Определить, какой конец отрезка будет неподвижным и принять за x другой конец отрезка.

2. Вычислить новое приближение к корню x по формуле (2) или (3).

3. Если длина отрезка [x , x ] не превосходит заданной точности, то процесс заканчивается и в качестве точного корня можно взять x или x , иначе идти к п.2

 

Решение одного варианта

1.Отделить корни графически и уточнить их методом хорд с точностью до 0.001: tg(0.5x+0.1)=x .

 

Отделим корень графически. Построим графики функций

y =tg(0.5x+0.1) и y =x :

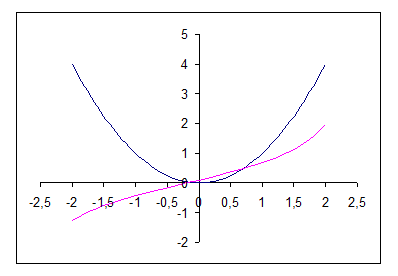
Таким образом, уравнение имеет два корня

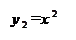x [0.5; 1] и x [-0.5; 0]

 

Чтобы уточнить этот корень методом хорд, определим знаки первой и второй производной функции f(x)= tg(0.5x+0.1)-x на промежутке [0.5;1]. Имеем

f ‘(x)=0.5/cos (0.5x+0.1)-2x;

f ‘(x)<0 при x [0.5; 1],

 

f‘’(x)=0.5sin(0.5x+0.1)/cos (0.5x+0.1)-2;

f ‘’(x) <0 при x [0.5; 1].

Для вычисления применяем формулу (3): x =а,

, где b=1, x =0,5

Вычисления удобно располагать в таблице:

n	x	f(x )
	0,5 0,608 0,642 0,650 0,652 0,653	0,100 0,034 0,009 0,002 0,001	-0,108 -0,034 -0,009 -0,002 0,000

x≈0,653.

 

Второй корень вычисляется по формуле (2) и равен –0,144

Ответ: x ≈0,653, x ≈-0,144.

2. Отделить корни аналитически и уточнить их методом хорд до 0,001:

.

Находим 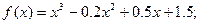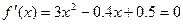D=0.16-6<0.

Составим таблицу знаков функции f(x):

x		-1
Знаки f(x)	-	-	+	+	+

Из таблицы видно, что уравнение имеет один действительный корень .

Уточним корень методом хорд.

при , , при

Для вычисления применяем формулу (2):

x =b x =a- , где а=-1, x =0.

N		f( )	h=
	-0,882 -0,943 -0,946 -0,946	1,5 0,216 0,010 0,000	-0,118 -0,057 -0,054 -0,054

 

 

Ответ: x≈-0,946.

 

Задания

1)Отделить корни графически и уточнить их методом хорд до 0.001:

1.

2. tg(0.58x+0.1)=x²­

3. ­_­­

4. tg(0.4x+0.4)=x²

5. lgx-7/(2x-6)=0

6.

7.

8.

9.

10.

11.

12.

13. x lgx - 1.2 = 0

14. 1.8x² – sin10x = 0

15. ctgx – x / 4 = 0

16. tg(0.3x + 0.4) = x²

17. x – 20sinx = 0

18. ctgx – x / 3 = 0

19. tg(0.47x + 0.2) = x²

20. x² + 4sinx = 0

21. ctgx – x / 2 = 0

22. 2x – lgx – 7 = 0

23. tg(0.44x + 0.3)=x²

24. 3x – cosx – 1 = 0

25. xsinx-1=0

26. 10cosx-0,1x²=0

27. 2lg(x+7)-5sinx=0

28. 1.2-lnx=4cos2x

2)Отделить корни аналитически и уточнить их методом хорд до 0.001:

1. x³ – 3x² + 9x – 8 = 0

2. x³ – 15x + 11 = 0

3. x³ – 3x² + 6x + 8 = 0

4. x³ – 0.1x² + 0.4x – 1.5 = 0

5. x³ – 3x² + 9x +2 = 0

6. x³ + x – 5 = 0

7. x³ + 0.2x² + 0.5x – 1.2 = 0

8. x³ + 3x +1= 0

9. x³ + 0.2x² + 0.5x – 2 = 0

10. x³ – 3x² + 12x – 9 = 0

11. x³ – 0.2x² + 0.3x – 1.2 = 0

12. x³ – 3x² + 6x – 2 = 0

13. x³ – 0.1x² + 0.4x – 1.5 = 0

14. x³ + 3x² + 6 = 0

15. x³ + 0.1x² + 0.4x – 1.2 = 0

16. x³ + 4x - 6 = 0

17. x³ + 0.2x² + 0.5x + 0.8 = 0

18. x³ - 3x² + 12x - 12 = 0

19. x³ – 0.2x² + 0.3x + 1.2 = 0

20. x³ - 2x + 4 = 0

21. x³ – 0.2x² + 0.5x - 1.4 = 0

22. x³ – 0.2x² + 0.5x – 1 = 0

23. x³ – 0.1x² + 0.4x + 1.2 = 0

24. x³ – 0.4x² + 0.6x – 1 = 0

25. 2x³-8x²-30x+1=0

26. 2x³-9x²-60x+1=0

27. x³-6x²+x+10=0

28. x³-4.5x²+x+3=0