 |
Главная |
Лабораторная работа №7. Решение систем линейных уравнений методом Гаусса
|
из
5.00
|
Решение систем линейных уравнений методом Гаусса
Краткая теория
Будем рассматривать системы уравнений вида
Аx=b (1)
Здесь А – квадратная матрица порядка n, x – вектор-столбец с n неизвестными компонентами  - вектор-столбец свободных членов.
- вектор-столбец свободных членов.
Решением системы называется любой вектор, при подстановке которого в систему получается верное равенство. Решить систему – значит определить, имеет ли она решение и, если решение есть, найти его с заданной точностью.
Приближенное решение системы линейных уравнений состоит из двух этапов:
1) нахождение приближенного значения;
2) уточнение решения.
Метод Гаусса
Один из методов решения системы (1) – метод Гаусса. Этот метод применим к любой системе линейных уравнений, определитель матрицы А которой отличен от нуля.
Алгоритм метода
Пусть имеется система линейных уравнений вида:
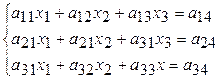
Разделим первое уравнение на коэффициент  , если
, если  , можно переставить уравнения системы так, чтобы первым оказалось уравнение с
, можно переставить уравнения системы так, чтобы первым оказалось уравнение с  . Получим уравнение вида
. Получим уравнение вида
 .
.
Умножим уравнение (*) на  и на
и на  и сложим их со вторым и третьим уравнениями системы. Получим систему уравнений:
и сложим их со вторым и третьим уравнениями системы. Получим систему уравнений:

Проделав те же преобразования с данной системой, получим уравнения:
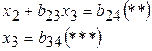
Из уравнений, отмеченных звездочками, найдем неизвестные 
Уточнение решения
Полученное методом Гаусса приближенное решение x0 содержит погрешность за счет округления приближенных значений. Тогда  , где
, где  - столбец поправок. Подставляя в систему, получим:
- столбец поправок. Подставляя в систему, получим:
Аx=b; A( 
 . Назовем А
. Назовем А  невязками и обозначим
невязками и обозначим  Тогда
Тогда 
Следовательно, чтобы найти невязки 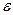 , надо подставить приближенное решение в систему и вычесть полученный столбец из столбца свободных членов. Для нахождения поправок следует снова решить систему, взяв в качестве столбца свободных членов столбец невязок. Поправки надо прибавить к приближенному решению.
, надо подставить приближенное решение в систему и вычесть полученный столбец из столбца свободных членов. Для нахождения поправок следует снова решить систему, взяв в качестве столбца свободных членов столбец невязок. Поправки надо прибавить к приближенному решению.
Решение одного варианта
Используя метод Гаусса, решите систему уравнений с точностью до 0,0001

Вычисления оформляем в таблице:
| Коэффициенты при неизвестных | Свободные члены | 
| 
| Невязки | |||||||||
| 0,14 0,24 -0,84 1,07 -0,83 0,56 0,64 0,43 -0,38 | 1,11 0,48 -0,83 |
|
|
| |||||||||
| 1 1,7143 -6,0000 -2,6643 6,9800 -0,6672 3,4600 | 7,9286 -8,0036 -5,9043 |
|
|
| |||||||||
| 1 -2,6198 1,7121 | 3,0040 -3,9000 |
|
|
| |||||||||
| -2,2779 -2,9637 -0.6582 |
|
|
|
Столбец  содержит суммы, вычисляемые по общему правилу,
содержит суммы, вычисляемые по общему правилу,  - строчные суммы,
- строчные суммы, 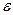 - невязки:
- невязки:

Уточнение корней:

Задание
Используя метод Гаусса, решить систему уравнений с точностью до 0,0001
1. 
2. 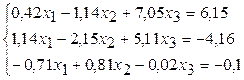
3. 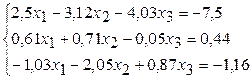
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 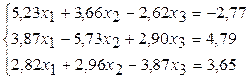
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 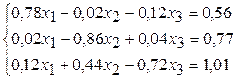
26. 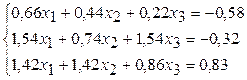
27. 
28. 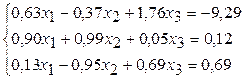
Лабораторная работа №8
Решение систем линейных уравнений методом простой итерации
Краткая теория
Будем рассматривать системы уравнений вида
Аx=b
Здесь А – квадратная матрица порядка n, x – вектор – столбец с n неизвестными компонентами  - вектор – столбец свободных членов.
- вектор – столбец свободных членов.
Решением системы называется любой вектор, при подстановке которого в систему получается верное равенство. Решить систему – значит определить, имеет ли она решение и, если решение есть, найти его с заданной точностью.
|
из
5.00
|
Обсуждение в статье: Лабораторная работа №7. Решение систем линейных уравнений методом Гаусса |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

