Метод сеток для уравнения гиперболического типа

Рассмотрим уравнение свободных колебаний однородной ограниченной струны (гиперболического типа) при отсутствии внешней силы

, (6)

где u=u(x,t) – смещение точки однородной струны с абсциссой х, t – время, а – постоянная, зависящая от физических свойств струны.

Будем искать решение уравнения (6) при заданных начальных и краевых условиях

(7)

и

(8)

Решим эту смешанную задачу методом сеток. Как и в случае параболического уравнения, покроем полосу , прямоугольной сеткой где

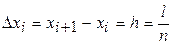(n – целое) и

На сетке 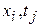приближенно заменим дифференциальное уравнение (6) соответствующим конечно-разностным уравнением.

Пользуясь симметричными формулами для производных, будем иметь

. (9)

При уравнение (9) упрощается и принимает вид ,

откуда . (10)

 

Решение одного варианта

1. Используя метод сеток, составить решение смешанной задачи для дифференциального уравнения параболического типа 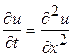(уравнение теплопроводности) при заданных начальных условиях

где 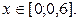Решение выполнить при для с четырьмя десятичными знаками, считая .

Параболическое уравнение решается методом сеток постепенным переходом от значений функции к значениям ; причем где

Вычисления производятся по формуле

Все расчеты приведены в таблице:

j	i
	xi tj		0,1	0,2	0,3	0,4	0,5	0,6
		0,12	0,39	0,60	0,75	0,84	0,87	0,84
	0,0017	0,1233	0,3800	0,5900	0,7400	0,8300	0,8600	0,84
	0,0033	0,1267	0,6372	0,5800	0,7300	0,8200	0,8517	0,84
	0,0050	0,1300	0,3659	0,5704	0,7200	0,8103	0,8445	0,84
	0,0067	0,1333	0,3607	0,5612	0,7101	0,8010	0,8380	0,84
	0,0083	0,1367	0,3562	0,5526	0,7004	0,7920	0,8322	0,84
	0,01	0,1400	0,3524	0,5445	0,6910	0,7834	0,8268	0,84

 

2. Используя метод сеток, составить решение смешанной задачи для уравнения колебания струны с начальными условиями и краевыми условиями 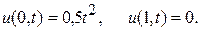Решение выполнить с шагом , определяя значения функции 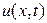с четырьмя десятичными знаками, причем .

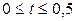Для решения воспользуемся соотношением

,

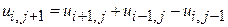где i=1,2,…; j=1,2,3,…

При этом а для определения можно использовать один из возможных приемов, например,

,

причем

.

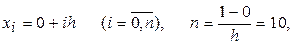
Кроме того,

Решая по указанным формулам удобно выполнять в таблице, которая и является решением данной задачи.

Порядок заполнения таблицы:

1. Вычисляем значения при 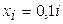и записываем их в первую строку (она соответствует значению t₀=0).

2. Вычисляем значения при и записываем их в первый столбец таблицы (он соответствует значению x₀=0).

xi tj		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
		0,198	0,384	0,546	0,672	0,75	0,768	0,714	0,576	0,342
0,1	0,005	0,2381	0,4247	0,5858	0,7092	0,7827	0,7942	0,7314	0,5824	0,3351
0,2	0,02	0,2317	0,4398	0,5878	0,6965	0,7533	0,7461	0,6626	0,4905	0,2404
0,3	0,045	0,2218	0,3948	0,5505	0,6320	0,6599	0,6218	0,5052	0,3206	0,1554
0,4	0,08	0,2082	0,3325	0,4390	0,5140	0,5004	0,4190	0,2798	0,1701	0,0802
0,5	0,125	0,1907	0,2523	0,2959	0,3074	0,2731	0,1584	0,0839	0,0393	0,0147

3. Заносим значения в последний столбец таблицы (он соответствует значению x₁₀=1,0)

4. Вычисляем значения по формуле , где и 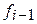берутся из первой строки таблицы, а . Результаты записываем во вторую строку таблицы.

5. Вычисляем значения в последующих строках по формуле , где значения берутся из двух предыдущих строк таблицы.

 

Задания

1. Используя метод сеток, составить решение смешанной задачи для дифференциального уравнения параболического типа 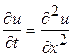(уравнение теплопроводности) при заданных начальных условиях

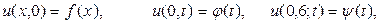
где Решение выполнить при для с четырьмя десятичными знаками, считая .

Вариант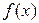
	cos2x	1-6t	0,3624
	x(x+1)	0	2t+0,96
	1,2+lg(x+0,4)	0,8+t	1,2
	sin2x	2t	0,932
	3x(2-x)	0	t+2,52
	1-lg(x+0,4)	1,4	t+1
	sin(0,55x+0,03)	t+0,03	0,354
	2x(1-x)+0,2	0,2	t+0,68
	sinx+0,08	0,08+2t	0,6446
	cos(2x+0,19)	0,932	0,1798
	2x(x+0,2)+0,4	2t+0,4	1,36
	lg(x+0,26)+1	0,415+t	0,9345
	sin(x+0,45)	0,435-2t	0,8674
	0,3+x(x+0,4)	0,3	6t+0,9
	(x-0,2)(x+1)+0,2	6t	0,84
	x(0,3+2x)	0	6t+0,9
	sin(x+0,48)	0,4618	3t+0,882
	sin(x+0,02)	3t+0,02	0,581
	cos(x+0,48)	6t+0,887	0,4713
	lg(2,63-x)	3(0,14-t)	0,3075
	1,5-x(1-x)	3(0,5-t)	1,26
	cos(x+0,845)	6(t+0,11)	0,1205
	lg(2,42+x)	0,3838	6(0,08-t)
	0,6+x(0,8-x)	0,6	3(0,24+t)
	cos(x+0,66)	3t+0,79	0,3058
	lg(1,43+2x)	0,1553	3(t+0,14)
	0,9+2x(1-x)	3(0,3-2t)	1,38
	lg(1,95+x)	0,29-6t	0,4065

2. Используя метод сеток, составить решение смешанной задачи для уравнения колебания струны с начальными условиями и краевыми условиями Решение выполнить с шагом , определяя значения функции 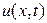с четырьмя десятичными знаками, причем .

Вариант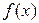
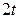
				-1
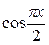
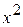
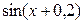
		2	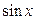0,3
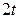
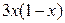
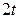
				1,5
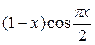
			2
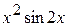
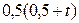
				2,25
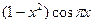
			0,5
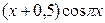
			0,5
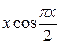
			0,4
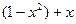
				0,9
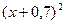
			0,5

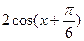
Литература

1. Вержбицкий В.М. Численные методы (линейная алгебра и нелинейные уравнения)/ В.М.Вержбицкий. – М.: «Высшая школа», 2000. – 266с.

2. Вержбицкий В.М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения)/ В.М.Вержбицкий. – М.: «Высшая школа», 2001. – 382 с.

3. Волков Е.А. Численные методы: учебное пособие/ Е.А.Волков. СПб.: Изд-во «Лань», 2004. – 256с.

4. Демидович Б.П. Основы вычислительной математики/ Б.П.Демидович, И.А. Марон. – М.: Изд-во «Наука», 1970. – 664с.

5. Демидович Б.П. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения: учебное пособие/ Б.П.Демидович, И.А.Марон, Э.З.Шувалова; Под ред. Б.П.Демидовича. – СПб.: Изд-во «Лань», 2008. – 400с.

6. Заварыкин В.М. Численные методы: учеб. пособие для студентов физ.-мат. спец. пед. ин-тов / В.М.Заварыкин, В.Г.Житомирский, М.П.Лапчик. – М.: Просвещение, 1990. – 176с.

7. Воробьева Г.Н. Практикум по численным методам/ Г.Н.Воробьева, А.Н. Данилова – М.: Высш. шк., 1979. – 184с.

8. Лапчик М.П. Численные методы: учебное пособие для студ. вузов / М.П.Лапчик, М.И.Рагулина, Е.К.Хеннер; Под ред.М.П.Лапчика. – М.: Издательский центр «Академия», 2005. – 384с.

9. Формалев В.Ф. Численные методы/ В.Ф.Формалев, Д.Л.Ревизников. – М.: ФИЗ-МАТЛИТ, 2004. – 400 с.

Содержание

Лабораторная работа №1. 1

Элементарная теория погрешностей. 2

Лабораторная работа №2. 6

Решение нелинейных уравнений методом половинного деления. 6

Лабораторная работа №3. 9

Решение нелинейных уравнений методом хорд. 9

Лабораторная работа №4. 12

Решение нелинейных уравнений методом касательных. 12

Лабораторная работа №5. 15

Решение нелинейных уравнений комбинированным методом хорд и касательных. 15

Лабораторная работа №6. 19

Решение нелинейных уравнений методом итерации. 19

Лабораторная работа №7. 21

Решение систем линейных уравнений методом Гаусса. 21

Лабораторная работа №8. 24

Решение систем линейных уравнений методом простой итерации. 24

Лабораторная работа №9. 30

Интерполяционный многочлен Лагранжа. 30

Лабораторная работа №10. 34

Интерполяционный многочлен Ньютона. 34

Лабораторная работа №11. 36

Обработка экспериментальных данных. 36

Лабораторная работа №12. 42

Численное интегрирование. 42

Лабораторная работа №13. 46

Метод Эйлера решения обыкновенных дифференциальных уравнений. 46

Лабораторная работа №14. 50

Решение дифференциальных уравнений в частных производных. 50

Литература. 55