Лабораторная работа №12

Численное интегрирование

Краткая теория

Для приближенного вычисления определенного интеграла , где 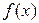- непрерывная на отрезке [a, b] функция, применяют различные квадратурные формулы. При этом подынтегральная функция заменяется на данном отрезке интегральным полиномом и применяется приближенное равенство:

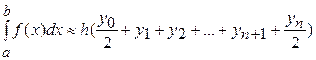или , (1)

где ; .

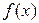Обозначив , для случая, когда дважды дифференцируема на [а,b], можно получить следующую оценку погрешности методом интегрирования по формуле трапеций:

, (2)

где ,

Формула Симпсона имеет вид:

(3)

Оценка погрешности, когда f(x) имеет четыре производных на [a,b], дается формулой:

, где , n=2m, (4)

Формула Симпсона обладает повышенной точностью по сравнению с формулой трапеций. Это означает, что для достижения той же точности в ней можно брать меньшее число отрезков разбиения. Для оценки погрешности на практике часто используется прием двойного пересчета. При этом интеграл вычисляется дважды: при делении промежутка интегрирования на n частей и на 2n частей.

Обозначаем полученные значения интеграла I_n и I_2n. Эти значения сравниваются, и совпадающие десятичные знаки считаются верными.

Обозначив через R_n и R_2n погрешность интегрирования по формуле Симпсона соответственно при n и 2n отрезках разбиения, можно получить оценку:

(5)

Решение одного варианта

1. Вычислить интеграл по формуле трапеций с точностью до 0.001

.

Чтобы вычислить интеграл с заданной точностью, следует подобрать значение ­n­ так, чтобы выполнялось условие:

, где ­ а­=0.6, b=1.4; M=max|f’’(x)|; .

Находим последовательно

; ;

; ­n=20 .

Дальнейшее вычисление выполняем в виде расчетной таблицы:

i	xi	y0, y20	y1,…, y19
	0,6	0,62017
	0,64		0,59256
	0,68		0,56687
	0,72		0,54297
	0,76		0,52072
	0,8		0,5
	0,84		0,48068
	0,88		0,46265
	0,92		0,44579
	0,96		0,43001
			0,41523
	1,04		0,40135
	1,08		0,38831
	1,12		0,37604
	1,16		0,36447
	1,2		0,35355
	1,24		0,34324
	1,28		0,33348
	1,32		0,32424
	1,36		0,31547
	1,4	0,30715
		0,92732	8,15761

 

 

 

 

2. Вычислить интеграл по формуле Симпсона при n=10. Оценить погрешность методом двойного пересчета.

 

 

Составим расчетную таблицу:

i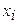
		-0.0559
	2.1		-0.0337
	2.2			-0.0142
	2.3		0.0027
	2.4			0.0172
	2.5		0.0297
	2.6			0.0401
	2.7		0.0488
	2.8			0.0559
	2.9		0.0651
		0.0657
		0.0098	0.1090	0.0991

 

 

Применяя формулу Симпсона,

получим

 

 

Для оценки погрешности повторим вычисление интеграла для n=20:

i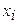
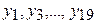
		-0.0559
	2.05		-0.0444
	2.1			-0.0337
	2.15		-0.0236
	2.2			-0.0142
	2.25		-0.0055
	2.3			0.0027
	2.35		0.0102
	2.4			0.0172
	2.45		0.0237
	2.5			0.0297
	2.55		0.0351
	2.6			0.0401
	2.65		0.0447
	2.7			0.0488
	2.75		0.0526
	2.8			0.0559
	2.85		0.0589
	2.9			0.0615
	2.95		0.0637
		0.0657
		0.0098	0.2155	0.208

 

 

Применяя формулу Симпсона,

получим

 

.

 

Задания

1) Вычислить интеграл по формуле с точностью до 0,001.

2) Вычислить интеграл по формуле Симпсона при n=10. Оценить погрешность методом двойного пересчета.

1.1)	2)	15.1)	2)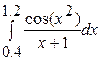
2.1)	2)	16.1)	2)
3.1)	2)	17.1)	2)
4.1)	2)	18.1)	2)
5.1)	2)	19.1)	2)
6.1)	2)	20.1)	2)
7.1)	2)	21.1)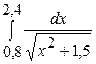	2)
8.1)	2)	22.1)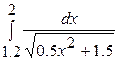	2)
9.1)	2)	23. 1)	2)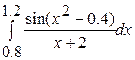
10.1)	2)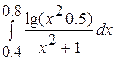	24.1)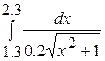	2)
11.1)	2)	25.1)	2)
12.1)	2)	26.1)	2)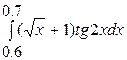
13.1)	2)	27.1)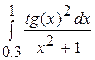	2)
14. 1)	2)	28.1)	2)

Лабораторная работа №13

Метод Эйлера решения обыкновенных дифференциальных уравнений

Краткая теория

Задача Коши: Найти решение y=y(x) дифференциального уравнения

, (1)

удовлетворяющее начальному условию . Решить дифференциальное уравнение (1) численным методом – это значит для заданной последовательности аргументов , ,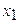…, , где , k= 0, 1,…,n и числа y₀ = y(x₀), не определяя функцию y=y(x), найти такие значения y₁, y₂, …, y_n, что y_k=y (x_k), k=1,2,…,n. Таким образом, численный метод решения дифференциального уравнения позволяет вместо нахождения функции y=y(x) получить таблицу значений этой функции для заданной последовательности аргументов.

Задача Коши имеет единственное решение, удовлетворяющее начальному условию, если функция f(x,y) непрерывна в некоторой окрестности точки (x₀,y₀) и если в этой окрестности существует ограниченная частная производная функции f по y.

Одним из численных методов решения дифференциальных уравнений является метод Эйлера. Пусть требуется найти решение задачи Коши на отрезке [a,b]. Разобьем отрезок [a,b] на n равных частей и получим последовательность x_k=x₀+hk, k=0,1,…,n; h=(b-a)/ n. Формула Эйлера для вычисления значений y имеет вид:

y_k+1=y_k+f (x_k, y_k)h (2)

y

 

 

 

M_n

 

M2

M₀ M₁

 

y₀ y₁ y₂

 

x₀ x₁ x₂ x_n x

 

Рис. 1

Геометрический смысл метода Эйлера состоит в следующем: на [x₀, x₁] искомую интегральную кривую заменяют отрезком касательной к ней, проходящей через точку M₀(x₀, y₀). Затем из точки M₁(x₁,y₁) проводят новый отрезок касательной уже к той интегральной кривой, которая проходит через M₁ (рис.1).

Продолжая построение отрезков, получают ломаную Эйлера, которая аппроксимирует искомую интегральную кривую.

Основным недостатком метода Эйлера является невысокая точность, поэтому чаще используют одну из модификаций метода Эйлера – метод Эйлера с уточнением. Согласно этому методу грубое приближение y⁽⁰⁾, найденное по формуле (2), уточняется в ходе построения итерационной последовательности

, где i=1,2,..- номер итерации. (3)

Итерации продолжают до тех пор, пока два последовательных приближения и не совпадут с требуемой степенью точности. После этого полагают

Решение одного варианта

Используя метод Эйлера с уточнением, составить таблицу приближенных значений решения дифференциального уравнения

,

удовлетворяющего начальному условию y(1.4)=2.2 на [1.4;2.4] с шагом h=0.1. Вычисления вести с четырьмя десятичными знаками.

Результаты вычислений оформим в виде таблицы 1. В заголовке таблицы приняты обозначения: k- номер аргумента x_k, для которого находится значение решения y_k, h- шаг изменения аргумента.

Порядок вычислений

1) Находим грубое приближение по формуле (2):

Значение f(x_k,y_k) записываем в 4- ый столбец таблицы. Затем вычисляем значение hf_k, а затем y⁰_k+1 по формуле (2) (сумма 3 и 5 столбцов таблицы).

 

2) Используя y⁰_k+1 в качестве начального приближения, находим уточнение значение y⁽ⁱ⁾_k+1 по формуле (3):

, где i – номер итерации.

Для этого вычисляем , записываем результат в 8-й столбец таблицы.

Находим сумму 4-го и 8-го столбцов (результат в 9-ый столбец). Умножаем результат на h/2 (10-ый столбец). Прибавив к значению 10 столбца значение y_k из 3-го столбца, получаем очередное значение итерационной последовательности (по формуле (3)) и записываем его в 7-ой столбец. Повторяем вычисления i-х приближений до тех пор, пока не будет выполнено равенство

до 4-х знаков после запятой, и берем в качестве очередного значения y_k (записываем в 3-ий столбец при следующем x_k).

3) Очередные значения y_k находим по правилам приведенных выше пунктов 1 и 2, пока не будут найдены все k решений на отрезке [a,b].

k					i
	1.4 1.5	2.2	2.2292	0.2229		2.4229 2.4305 2.4306	2.3805 2.3821	4.6097 4.6113	0.2305 0.2306
	1.5 1.6	2.4306	2.3821	0.2382		2.6688 2.6760 2.6761	2.5268 2.5280	4.9089 4.9101	0.2454 0.2455
	1.6 1.7	2.6761	2.5281	0.2528		2.9289 2.9357 2.9357	2.6641 2.6648	5.1922 5.1929	0.2566 0.2566
	1.7 1.8	2.9357	2.6648	0.2665		3.2022 3.2084 3.2084	2.7892 2.7895	5.4540 5.4543	0.2727 0.2727
	1.8 1.9	3.2084	2.7895	0.2790		3.4874 3.4929 3.4929	2.8998 2.8998	5.6893 5.6893	0.2845 0.2845
	1.9 2.0	3.4929	2.8998	0.2900		3.7829 3.7876 3.7876	2.9939 2.9936	5.8937 5.8934	0.2947 0.2947
	2.0 2.1	3.7876	2.9936	0.2994		4.0870 4.0908 4.0908	3.0700 3.0696	6.0636 6.0632	0.3032 0.3032
	2.1 2.2	4.0908	3.0696	0.3070		4.3978 4.4006 4.4006	3.1273 3.1268	6.1969 6.1964	0.3098 0.3098
	2.2 2.3	4.4006	3.1268	0.3127		4.7133 4.7152 4.7152	3.1658 3.1654	6.2968 6.2922	0.3146 0.3146
	2.3 2.4	4.7152	3.1654	0.3165		5.0517 5.0328 5.0328	3.1866 3.1863	6.3520 6.3517	0.3176 0.3176
	2.4	5.0328

Задание

Используя метод Эйлера с уточнением, составить таблицу приближенных значений интеграла дифференциального уравнения удовлетворяющего начальным условиям 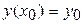на отрезке [a,b]; шаг h=0.1.

Все вычисления вести с четырьмя десятичными знаками.

1. ,

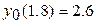
2. ,

3. ,

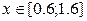
4. ,

5. ,

6. ,

7. ,

8. ,

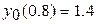
9. ,

10. ,

11. ,

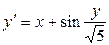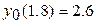
12. ,

13. ,

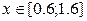
14. ,

15. ,

16. ,

17. ,

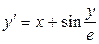18. ,

19. ,

20. ,

21. ,

22. ,

23. ,

24. ,

25. ,

26. ,

27. ,

28. ,

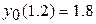
29. ,

30. ,