 |
Главная |
Лекция 22-23. Комплексные числа
|
из
5.00
|
Определение. Комплексным числом zназывается выражение 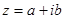 , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:
, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением: 
При этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).
Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.
Определение. Числа 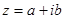 и
и 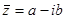 называются комплексно – сопряженными.
называются комплексно – сопряженными.
Определение. Два комплексных числа  и
и 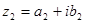 называются равными, если соответственно равны их действительные и мнимые части:
называются равными, если соответственно равны их действительные и мнимые части: 
Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части. 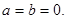
Комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.
Тригонометрическая форма числа
Из геометрических соображений видно, что 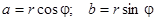 . Тогда комплексное число можно представить в виде:
. Тогда комплексное число можно представить в виде: 
Такая форма записи называется тригонометрической формой записи комплексного числа.
При этом величина r называется модулемкомплексного числа, а угол наклона j -аргументомкомплексного числа.
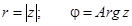 . Из геометрических соображений видно:
. Из геометрических соображений видно:
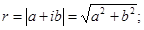

Очевидно, что комплексно – сопряженные числа имеют одинаковые модули и противоположные аргументы. 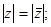
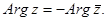
Действия с комплексными числами
Сложение и вычитание
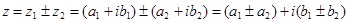
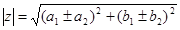
Умножение


В тригонометрической форме:
 ,
, 
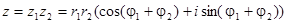
В случае комплексно – сопряженных чисел:

Деление 
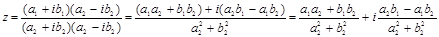
В тригонометрической форме:
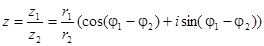
Возведение в степень
Из операции умножения комплексных чисел следует, что

В общем случае получим: 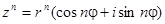 , где n – целое положительное число. Это выражение называется формулой Муавра
, где n – целое положительное число. Это выражение называется формулой Муавра
Извлечение корня из комплексного числа
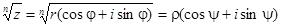
Возводя в степень, получим:
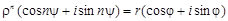 . Отсюда:
. Отсюда: 
 ,
, 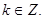
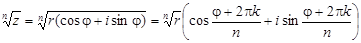
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.
Показательная форма комплексного числа
Рассмотрим показательную функцию 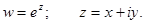 Можно показать, что функция w может быть записана в виде:
Можно показать, что функция w может быть записана в виде: 
Данное равенство называется уравнением Эйлера.Вывод этого уравнения будет рассмотрен позднее.
Для комплексных чисел будут справедливы следующие свойства: 1) 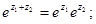 2)
2) 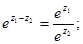 3)
3)  где m – целое число.
где m – целое число.
Если в уравнении Эйлера показатель степени принять за чисто мнимое число (х=0), то получаем: 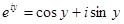
Для комплексно – сопряженного числа получаем:
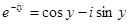 . Из этих двух уравнений получаем:
. Из этих двух уравнений получаем: 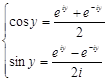
Если представить комплексное число в тригонометрической форме: 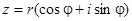
и воспользуемся формулой Эйлера: 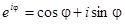
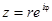
Полученное равенство и есть показательная форма комплексного числа.
Разложение многочлена на множители
Определение. Функция вида f(x) 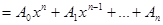 называется целой рациональной функцией от х.
называется целой рациональной функцией от х.
Теорема Безу. При делении многочлена f(x) на разность x – a получается остаток, равный f(a).
Следствие. Если, а – корень многочлена, т.е. f(a) = 0, то многочлен f(x) делится на (х – а) без остатка.
Определение. Если уравнение имеет вид Р(х) = 0, где Р(х) – многочлен степени n, то это уравнение называется алгебраическим уравнением степени n.
Теорема. (Основная теорема алгебры) Всякая целая рациональная функция f(x) имеет, по крайней мере, один корень, действительный или комплексный.
Теорема. Всякий многочлен n – ой степени разлагается на n линейных множителей вида (x – a) и множитель, равный коэффициенту при xn.
Теорема. Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого.
Если среди корней многочлена встречаются кратные корни, то разложение на множители имеет вид:


ki - кратность соответствующего корня.
Отсюда следует, что любой многочлен n – ой степени имеет ровно n корней (действительных или комплексных).
|
из
5.00
|
Обсуждение в статье: Лекция 22-23. Комплексные числа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

