 |
Главная |
Лекция 25. Основные методы интегрирования
|
из
5.00
|
Замена переменной интегрирования
При нахождении многих интегралов оказывается эффективной следующая идея: вместо исходной переменной х вводят новую переменную по формуле  или
или  (где φ- дифференцируемая функция) таким образом, чтобы относительно новой переменной интеграл был значительно проще, вычисляют этот преобразованный интеграл, а затем возвращаются к старой переменной.
(где φ- дифференцируемая функция) таким образом, чтобы относительно новой переменной интеграл был значительно проще, вычисляют этот преобразованный интеграл, а затем возвращаются к старой переменной.
Если f(x)- непрерывная функция, F(x)- её первообразная, а φ(х)- дифференцируемая функция, то изложенная идея выглядит так:

В частном случае 
Этот факт можно сформулировать в виде правила: Если в числителе стоит производная знаменателя, то интеграл равен натуральному логарифму модуля знаменателя.
Интегрирование по частям
Суть метода заключается в использовании формулы

Для применения этой формулы подынтегральное выражение следует представить в виде произведения одной функции и на дифференциал другой dv. При переходе от левой части формулы к её правой части мы должны функцию и дифференцировать, а выражение dv- интегрировать.
Интегрирование иррациональных функций
1. Если корни в подынтегральном выражении имеют вид: 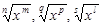 , то оно преобразуется в рациональную дробь с помощью подстановки
, то оно преобразуется в рациональную дробь с помощью подстановки  , где k- наименьшее общее кратное показателей корней, т. е. чисел n,q,s.
, где k- наименьшее общее кратное показателей корней, т. е. чисел n,q,s.
2. Если выражение под знаком интеграла содержит только корни  , то оно приводится к рациональной дроби с помощью подстановки
, то оно приводится к рациональной дроби с помощью подстановки  , где k- наименьшее общее кратное показателей корней, т. е. чисел n,q,s.
, где k- наименьшее общее кратное показателей корней, т. е. чисел n,q,s.
3. Если выражение под знаком интеграла содержит только корни  , то оно приводится к рациональной дроби с помощью подстановки
, то оно приводится к рациональной дроби с помощью подстановки  , где k- наименьшее общее кратное показателей корней, т. е. чисел n,q,s.
, где k- наименьшее общее кратное показателей корней, т. е. чисел n,q,s.
4. Если подынтегральное выражение представляет собой дифференциальный бином, т. е. выражение вида  , где т, п, р –рациональные числа, то данный интеграл сводится к интегралу от рациональной дроби в следующих трёх случаях:
, где т, п, р –рациональные числа, то данный интеграл сводится к интегралу от рациональной дроби в следующих трёх случаях:
а) При р- целом - подстановка  , где k- общий знаменатель дробей т и п.
, где k- общий знаменатель дробей т и п.
б) При  целом – подстановка
целом – подстановка  , где k- знаменатель числа р
, где k- знаменатель числа р
в) При  целом – подстановка
целом – подстановка  , где k- знаменатель числа р.
, где k- знаменатель числа р.
Интегрирование тригонометрических функций
1. Если под знаком интеграла стоит выражение  , получающееся из функций
, получающееся из функций  и некоторых констант с помощью четырёх арифметических действий, то данный интеграл
и некоторых констант с помощью четырёх арифметических действий, то данный интеграл  сводится к интегралу от рациональной дроби при помощи универсальной подстановки
сводится к интегралу от рациональной дроби при помощи универсальной подстановки  , в этом случае
, в этом случае  .
.
2. Если  =
=  , то целесообразно применить подстановку
, то целесообразно применить подстановку  .
.
3. Если  = -
= -  , то интеграл рационализуется с помощью подстановки
, то интеграл рационализуется с помощью подстановки  .
.
Если же  =-
=-  , то интеграл рационализуется с помощью подстановки
, то интеграл рационализуется с помощью подстановки  .
.
4. Если  , где т и п –четные неотрицательные числа, то применимы формулы:
, где т и п –четные неотрицательные числа, то применимы формулы:  ,
, 
5. При вычислении интегралов  ,
,

пользуются тригонометрическими формулами:



Интегралы вида  вычисляются с помощью формул
вычисляются с помощью формул  и
и  , позволяющих понизить степень тангенса и котангенса.
, позволяющих понизить степень тангенса и котангенса.
|
из
5.00
|
Обсуждение в статье: Лекция 25. Основные методы интегрирования |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

