 |
Главная |
Проверка нормальности закона распределения вероятности результата измерения
|
из
5.00
|
При обработке экспериментальных данных существенное значение имеет вопрос о том, подчиняется или нет результат измерения нормальному закону распределения вероятности. Непротиворечивость такой гипотезы должна быть обязательно проверена.
Поскольку ошибки искажают эмпирический закон распределения вероятности результата измерения, постольку проверка предположения о его нормальности производится после исключения ошибок.
Правдоподобна или нет гипотеза о том, что результат измерения подчиняется нормальному закону распределения вероятности, можно определить уже по виду гистограммы, построенной на основании экспериментальных данных. Наглядность отображения гистограммой закона распределения вероятности результата измерения зависит от соблюдения следующих правил при ее построении:
1) интервалы DQ, на которые разбивается ось абсцисс, следует выбирать, по возможности, одинаковыми;
2) число интервалов k устанавливать в соответствии со следующими рекомендациями:
Число измерений Рекомендуемое число интервалов
40 – 100 7 – 9
100 – 500 8 – 12
500 – 1000 10 – 16
1000 – 10000 12 – 22
3) масштаб гистограммы выбирать так, чтобы ее высота относилась к основанию, примерно, как 5 к 8.
Иногда по виду гистограммы можно с большой уверенностью заключить, что результат измерения подчиняется (или не подчиняется) нормальному закону распределения вероятности. Если, например, гистограмма имеет вид, показанный на рис. 3. а, то результат измерения определенно не подчиняется нормальному закону. Если же гистограмма имеет вид, показанный на рис. 3. б, то возникает сомнение: достаточно ли хорошо она соответствует теоретической кривой нормального закона распределения плотности вероятности, показанной пунктиром? Для разрешения этого сомнения нужно иметь правило, руководствуясь которым можно было бы принимать то или иное решение.

Рисунок 3 – Гистограммы, построенные по экспериментальным данным
Существует несколько так называемых критериев согласия,по которым проверяются гипотезы о соответствии экспериментальных данных тому или иному закону распределения вероятности результата измерения. Наиболее распространенным из них является критерий К. Пирсона. При использовании этого критерия за меру расхождения экспериментальных данных с теоретическим законом распределения вероятности результата измерения принимается сумма квадратов отклонения частостей mi/n от теоретической вероятности Pi попадания отдельного значения результата измерения в i-й интервал, причем каждое слагаемое берется с коэффициентом n/Pi:

|

Рисунок 4 – Интегральная функция распределения вероятности
К. Пирсона
Если расхождение случайно, то c2 подчиняется c2 – распределению (распределению К. Пирсона). Кривые интегральной функции этого распределения представлены на рис. 4 (здесь k соответствует числу интервалов только при проверке соответствия закона распределения вероятности результата измерения нормальному закону). Интегральная функция определяет вероятность того, что случайное число примет значение меньшее аргумента этой функции. Поэтому, задавшись значением интегральной функции распределения К. Пирсона F(c20), можно проверить, больше или меньше ее аргумента c20 (см. рисунок 4) вычисленное значение c2. Если меньше, то с выбранной вероятностью c2 можно считать случайным числом, подчиняющимся c2 – распределению К. Пирсона, т.е. признать случайным расхождение между эмпирической и теоретической плотностью распределения вероятности результата измерения. Если же окажется, что c2>c20, то с той же вероятностью придется признать, что c2 не подчиняется распределению К. Пирсона, т.е. гипотеза о соответствии эмпирического закона распределения вероятности теоретическому не подтверждается.
Пример 3. 100 независимых числовых значений результата измерения напряжения цифровым вольтметром, каждое из которых повторилось m раз, приведены в первой графе таблице 2.
Проверить гипотезу о том, что результат измерения подчиняется нормальному закону распределения вероятности.
Решение
1. Используя результаты вспомогательных вычислений, сведенные в третьей графах, найдем стандартное отклонение результата измерения: 
2. Используя результаты вспомогательных вычислений в четвертой, пятой и шестой графах, найдем стандартное отклонение результата измерения: 
3. Ни одноиз значений результата измерения не отличается от среднего арифметического больше чем на 3SU=0,381. Можно считать, что ошибок нет.
4. При использовании критерия К. Пирсона в каждом интервале должно быть не меньше пяти независимых значений результата измерения. В соответствии с этим образуем интервалы так, как это представлено во второй графе табл. 3.
Таблица 2 – Результаты измерения напряжения цифровым вольтметром
| U | m | mU | 
| 
| 
|
| 8,30 8,35 8,40 8,45 8,50 8,55 8,60 8,65 8,70 8,75 8,80 8,85 8,90 8,95 | 8,30 16,70 33,60 42,25 68,00 85,50 154,80 147,05 104,40 78,75 61,60 53,10 – 8,95 | -0,33 -0,28 -0,23 -0,18 -0,13 -0,08 -0,03 0,02 0,07 0,12 0,17 0,22 – 0,32 | 0,1089 0,0784 0,0529 0,0324 0,0169 0,0064 0,0009 0,0004 0,0049 0,0144 0,0289 0,0484 – 0,1024 | 0,1089 0,1568 0,2116 0,1620 0,1352 0,0640 0,0162 0,0068 0,0588 0,1296 0,2023 0,2904 – 0,1024 |
Таблица 3 – Расчетные данные при использовании критерия
К. Пирсона
| i | Интервалы | mi | ti | L(ti) | Pi | mi-nPi | 
| |
| (Ui-1; | Ui) | |||||||
| (-¥; (8,425; (8,475; (8,525; (8,575; (8,625; (8,675; (8,725; (8,775; (8,825; | 8,425) 8,475) 8,525) 8,575) 8,625) 8,675) 8,725) 8,775) 8,825) +¥) | -1,614 -1,220 -0,827 -0,433 -0,039 0,354 0,748 1,142 1,536 +¥ | -0,4467 -0,3888 -0,2959 -0,1676 -0,0156 6,1383 0,2728 0,3733 0,4377 0,5000 | 0,0533 0,0579 0,0929 0,1283 0,1520 0,1539 0,1345 0,1005 0,0644 0,0623 | 1,67 -0,79 -1,29 -2,83 2,80 1,61 -1,45 -1,05 0,56 0,77 | 0,523 0,108 0,179 0,624 0,516 0,168 0,157 0,110 0,048 0,095 |
5. Определим, на сколько SU отстоит от среднего арифметического, правая Ui граница каждого интервала:
 . .
|
Полученные значения параметра t внесем в четвертую графу таблицы 3.
6. По значению ti из графика на рис. 5 можно определить, с какой вероятностью отдельное значение результата измерения, подчиняющегося нормальному закону распределения вероятности, попадает в интервал  . С вероятностью в два раза меньшей оно попадает в левую или правую половину этого интервала. Эта вероятность определяется интегралом вероятности – функцией Лапласа L(ti), так что для повышения точности расчетов можно пользоваться не графиком, а таблицами функции Лапласа. Полученные из таблиц значения L(ti) занесены в пятую графу табл. 3.
. С вероятностью в два раза меньшей оно попадает в левую или правую половину этого интервала. Эта вероятность определяется интегралом вероятности – функцией Лапласа L(ti), так что для повышения точности расчетов можно пользоваться не графиком, а таблицами функции Лапласа. Полученные из таблиц значения L(ti) занесены в пятую графу табл. 3.
7. Теоретическая вероятность Pi, попадания в i-й интервал отдельного значения результата измерения, подчиняющегося нормальному закону распределения вероятности, очевидно равна

|
Принимая во внимание, что L(-¥)=-0,5, а L(¥)=0,5, поместим рассчитанные значения Рi в шестую графу табл. 3.
8. В седьмую и восьмую графы внесены результаты остальных вспомогательных вычислений. Суммирование чисел в восьмой графе дает 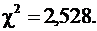
9. Из графика на рис. 4 видно, что рассчитанное значение
c2<<c20, соответствующего, например, вероятности 0,95. Таким образом, можно принять гипотезу о том, что результат измерения подчиняется нормальному закону.

Рисунок 5 – Вероятность попадания отдельного значения результата
измерения в окрестность среднего значения
Критерий согласия К. Пирсона широко применяется для проверки гипотез о том, что результат измерения подчиняется вполне определенному закону распределения вероятности. При c2<c20 соответствующая гипотеза принимается, при c2³c20 – отвергается. Однако даже выполнение неравенства c2<<c20 не может служитьдоказательством того, что результат измерения подчиняется этому закону распределения вероятности.
При использовании критерия К. Пирсона, как и в случае применения других критериев, возможны два рода ошибок. Ошибка первого рода состоит в отклонении верной гипотезы, а ошибка второго рода – в принятии неправильной. Для иллюстрации на рис. 6 показаны кривые плотности распределения вероятности величины c2 в случаях, когда проверяемая гипотеза верна – кривая 1, и когда неверна – кривая 2. Если вероятности, с которой выносится решение, соответствует значение c20, то при всех c2<c20, гипотеза будет приниматься, а при всех c2³c20 – отклоняться.
Вероятности ошибок первого и второго родов при этом:

|
Обе они зависят от значения c20, которое в свою очередь определяется вероятностью P=F(c20), с которой принимается решение. С повышением этой вероятности значение c20 увеличивается, вероятность ошибки первого рода уменьшается, а ошибки второго рода – возрастает, и наоборот. Таким образом, нецелесообразно принимать решение с очень высокой степенью вероятности. Обычно Р выбирается равной 0,9...0,95.

Рисунок 6 – Графики плотности распределения вероятности c2 в случаях,
когда проверяемая гипотеза верна (1) и неверна (2)
При проверке нормальности закона распределения вероятности результата измерения применение критерия К. Пирсона дает хорошие результаты только, если n>40...50. При 10...15<n<40...50 применяется так называемый составной критерий. Сначала рассчитывается

|
и проверяется выполнение условия

|
где dmin и dmax зависят от вероятности Р*,с которой принимается решение, и находятся по табл. 4.
Таблица 4 – Данные для использования составного критерия
| п | Р* = 0,90 | Р* = 0,95 | Р* = 0,99 | |||
| dmin | dmax | dmin | dmax | dmin | dmax | |
| 0,7409. | 0,8899 | 0,7153 | 0,9073 | 0,6675 | 0,9359 | |
Если это условие соблюдается, то дополнительно проверяются «хвосты» теоретического и эмпирического законов распределения вероятности. При 10£n£20 считается допустимым отклонение одного из независимых значений результата измерения Qi от среднего арифметического больше, чем на 2,5SQ, при 20<n£50 – двух, что соответствует доверительной вероятности P**»0,98.
Несоблюдения хотя бы одного из двух условий достаточно для того, чтобы гипотеза о нормальности закона распределения вероятности результата измерения была отвергнута. В противном случае гипотеза принимается с вероятностью Р>Р*+Р**–1.
При n<10...15 гипотеза о том, что результат измерения подчиняется нормальному закону распределения вероятности, не проверяется. Решение принимается на основании анализа априорной информации.
|
из
5.00
|
Обсуждение в статье: Проверка нормальности закона распределения вероятности результата измерения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

